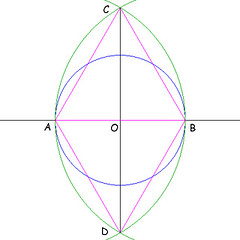
Sia dato il cerchio con diametro AB. Puntando il compasso in A, tracciare un arco di raggio AB; e puntando in B, un arco dello stesso raggio: i due archi si incontrano nei punti C e D. Congiungendo i punti CD, si determina il punto O: tale punto è il centro del cerchio dato, e il segmento CD è perpendicolare al diametro AB.
Infatti congiungendo i punti AC, AD, BCe BD (linee viola) è ovvio che assieme al diametro AB otteniamo due triangoli equilateri, in quanto ogni segmento è uguale al diametro del cerchio dato. Ma sono anche uguali i quattro triangoli che hanno un vertice in O: prendiamo in considerazione i triangoli di sinistra, ACO e ADO; i lati AC e AD sono uguali; il lato AO è in comune, e gli angoli in A sono entrambi di 60° in quanto vertici di triangoli equilateri. Lo stesso discorso vale per tutte le altre coppie di triangoli adiacenti.
Ora, se questi quattro triangoli sono uguali fra loro, sono uguali anche i segmenti AO e OB. Quindi il punto O, che è sul diametro del cerchio dato, ed è equidistante dalle intersezioni del cerchio con il diametro, è il centro del cerchio. Inoltre la retta CD è perpendicolare alla AB, in quanto (X definizione del libro I degli Elementi di Euclide):
"Quando una retta innalzata su un'altra retta forma gli angoli adiacenti uguali fra loro, ciascuno dei due angoli uguali è retto, e la retta innalzata si chiama perpendicolare a quella su cui è innalzata."
Ecco l'animazione del procedimento:
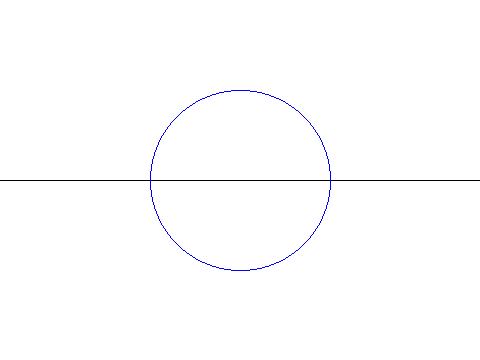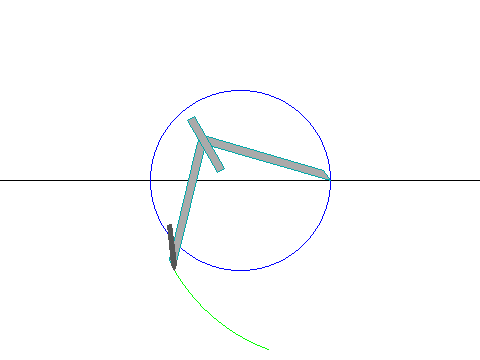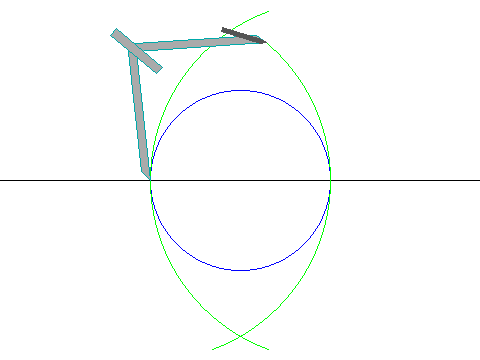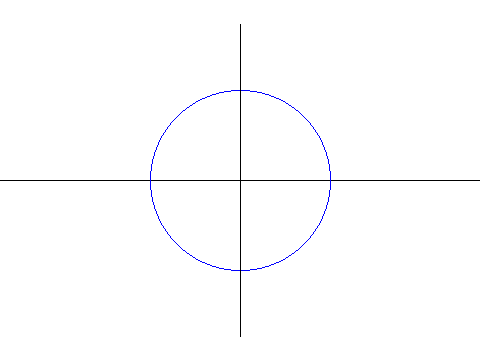
Nessun commento:
Posta un commento