Sommario:
– Contare
I numeri "Primitivi"
Contare
I "Calcoli"
Addizione
Sottrazione
Moltiplicazione
Divisione
Estrazione di radice
Una provocazione!
+ Sistemi di numerazione
+ Addizione e Sottrazione
+ Moltiplicazione
+ Divisione
+ Radice Quadrata
+ Elevamento a potenza
+ Logaritmi
+ Il Regolo Calcolatore
I numeri "Primitivi"
Siamo tutti abituati a parlare di "Numeri Naturali"... ma questa è una definizione ormai matura, identificata da matematici / filosofi che sapevano esattamente di cosa stavano parlando!
La storia dell'aritmetica non si sa proprio quando sia cominciata: la prima evidenza storica di un qualche modo di contare risale al Paleolitico superiore, cioè tra il 20.000 a.C. e il 18.000 a.C.: si tratta dell'Osso d'Ishango, un osso ricoperto da una serie di scalfitture raggruppate in vario modo, e con una scaglia di quarzo tagliente innestata ad una estremità probabilmente utilizzata per praticare le incisioni. Secondo alcuni scienziati potrebbe avere avuto una funzione anche più complessa del semplice contare qualcosa.
"Contare": assieme alla costruzione di utensili e all'uso della parola, è sicuramente una di quelle attività che distingue l'essere umano dagli altri animali. Ora qualcuno potrebbe obiettare che anche alcuni animali sanno distinguere gruppi di oggetti più numerosi da quelli meno numerosi; ma non contano affatto: l'operazione di contare significa associare i nomi generici uno, due, tre... a oggetti sempre diversi; e ci vuole una bella capacità di astrazione per capire che la serie dei "nomi" uno, due, tre... va bene per contare qualsiasi cosa: oggi do il nome "uno" a una mela, domani lo darò... a una moglie, e così via.
Gli uomini hanno imparato a comunicare fra loro cose come "tre capre" e "tre mele": sono concetti che rappresentano gruppi di cose diverse, che hanno in comune una ben precisa indicazione di quantità. Ma c'è voluto un enorme lavoro intellettivo per dominare il concetto di numero, passando dall'idea primitiva alla compiuta comprensione dei numeri, e soprattutto dell'infinito: quest'ultimo concetto è stato affrontato con successo solo verso la metà del XIX secolo! ▲
Contare
L'operazione del contare non è un'operazione banale neanche per noi "moderni", infatti quando ci troviamo in difficoltà... usiamo le dita delle mani:
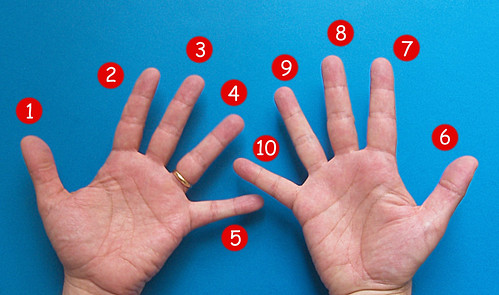
ecco perché quasi tutti i sistemi di numerazione sono sempre stati quinari o decimali. Di questo si ha evidenza perché, ovviamente, a un certo punto l'uomo ha cercato il modo di trascrivere il risultato dei propri conteggi; e sono stati trovati vari modi di scrivere i numeri: tutti basati sul 5 e sul 10 (e anche sul 20... che qualcuno abbia usato anche i diti dei piedi?). Per noi è usuale segnare i punti, o contare altri piccoli numeri, in questo modo:

di solito raggruppiamo i punti di cinque in cinque, per cui a colpo d'occhio sappiamo che qui sopra abbiamo contato fino a 12.
L'abilità di contare è legata all'abilità di trascrivere i risultati ottenuti; e in questo senso l'essere umano si è sbizzarrito in una serie infinita di sistemi diversi, da quelli più rozzi a quelli più sorprendenti, come quello babilonese: ne parlerò nel prossimo capitolo. ▲
I "Calcoli"
L'operazione del contare non è certo sufficiente per risolvere tutti i problemi aritmetici; comunque, anche solo contando, si possono svolgere parecchie operazioni di calcolo.
Il termine "calcolo" deriva dal latino calculus, che vuol dire pietruzza: sicuramente pietruzze, o semi, o altri piccoli oggetti sono stati il primo sistema per fare di conto. Quindi muniamoci di una scodella e di un adeguato numero di sassolini, e cominciamo a darci da fare! ▲
Addizione
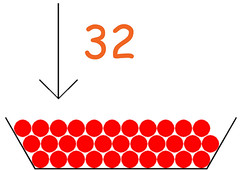
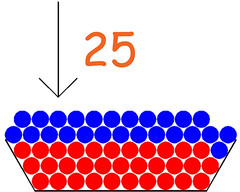
Ammettiamo di dover sommare i numeri 32 e 25: conto 32 sassolini mettendoli dentro alla scodella; ne conto altri 25; alla fine conto quanti sassolini ci sono nella scodella: se non ho commesso errori, non posso che contarne 57: ▲
Sottrazione
Se voglio sottrarre 17 da 65 basta che nella mia scodella io inserisca 65 sassolini; poi ne tolgo 17, contandoli, infine conto quanto sassolini sono rimasti:
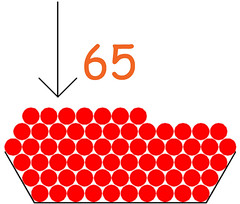
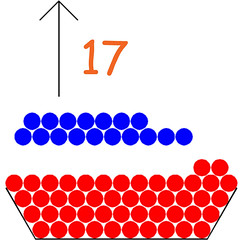
Una soluzione più "creativa", ma sempre di conteggio si tratta, consiste in questo: metto i sassolini nella scodella contando da 18. Se metto il primo sassolino contando 18, poi il secondo contando 19 e così via fino al 65, alla fine i sassolini nella scodella non potranno che essere 48. ▲
Moltiplicazione
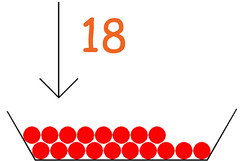
Dovendo moltiplicare 4 x 18, inserisco nella scodella 4 volte diciotto sassolini, infine conto il contenuto (72). ▲
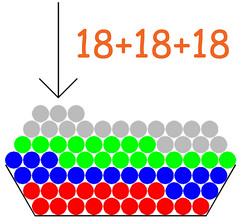
Calcolo del quadrato.
Come per la moltiplicazione! Un esempio: se voglio sapere quante uova ci sono in un cartone da 12 x 12, basta contarle! ▲
Calcolo del cubo.
Proviamo con il numero 6. Grazie al calcolo del quadrato, scopro che 6 x 6 fa 36. Metto 6 volte 36 sassolini nella scodella, e alla fine conto! (216). Per tornare all'esempio delle uova: se ne acquisto una scatola da 12 cartoni di 12 x 12 (totale 1728), non occorre fare molti calcoli: basta contarle! ▲
Divisione
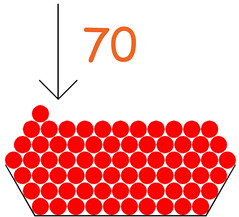
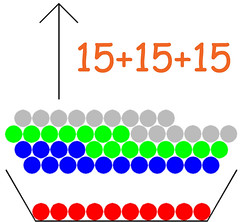
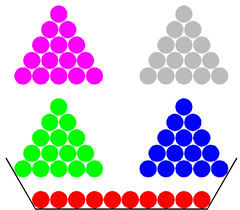
Ammettiamo di voler dividere 70 per 15. Metto 70 sassolini nella scodella, poi ne tolgo 15 per volta facendone dei mucchietti: alla fine mi ritrovo con quattro mucchietti (quoziente) e un avanzo di dieci sassolini (resto). ▲

Estrazione di radice
Posso fare per tentativi. Ammettiamo di voler calcolare la radice di 55: provo a calcolare 5², e vedo che il risultato è minore (25) del numero dato; poi con 6² (36), con 7² (49) e infine 8²: il risultato è 64, quindi maggiore del 55 di cui volevo calcolare la radice; allora la radice di 55 è 7 (almeno per quanto riguarda la parte intera). ▲
Una provocazione!
Insomma abbiamo scoperto che solo contando... si copre il programma d'insegnamento di aritmetica di praticamente tutte le elementari! ▲
Prossimo capitolo: Sistemi di Numerazione
How to get the game of the day to play the casino site
RispondiEliminaStep 1: Select one luckyclub.live of the three options to play the game of the day, and click on a button next to it.