Euclide: il "Primo" Teorema

Sommario:

+ Gli Elementi di Euclide
– Euclide: Il "Primo" Teorema
      Un po' di confusione?
      Elementi, Libro I, Proposizione 47
+ Euclide: Il "Secondo" Teorema

Un po' di confusione?

Nel corso di studi delle scuole medie vengono solitamente insegnati il Primo e il Secondo Teorema di Euclide, creando però una certa confusione filologica. In particolare l'enunciato del Primo Teorema ci viene esposto così:

In un triangolo rettangolo il quadrato costruito su un cateto è equivalente al rettangolo avente per dimensioni l'ipotenusa e la proiezione di quel cateto sull'ipotenusa stessa.

Ebbene, questo enunciato negli Elementi di Euclide non esiste, ma la sua dimostrazione è compresa nella proposizione che segue.   ▲  

Elementi, Libro I, Proposizione 47

Nei triangoli rettangoli il quadrato del lato opposto all'angolo retto è uguale alla somma dei quadrati che comprendono l'angolo retto.

Risulta evidente che si tratta dell'enunciato del Teorema di pitagora, ma Euclide non lo affronta occupandosi direttamente dell'intero quadrato costruito sull'ipotenusa; quest'ultimo viene piuttosto diviso in due rettangoli:



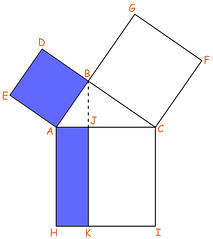
Dato il triangolo ABC rettangolo in B, Euclide traccia l'altezza da B sull'ipotenusa AC, trovando il punto J (detto in altre parole, il segmento AJ è la proiezione del cateto AB sull'ipotenusa). In base a questo punto divide il quadrato ACIH nei due rettangoli AJKH e JCIK: secondo il primo teorema di Euclide l'area del quadrato costruito sul cateto AB, e l'area del rettangolo che ha per lati l'ipotenusa e la proiezione del cateto AB sull'ipotenusa (le aree indicate in blu) sono equivalenti.



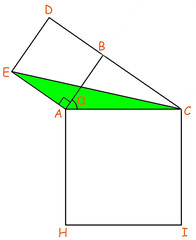
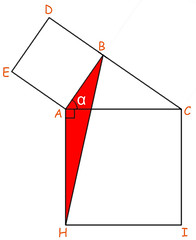
I triangoli verde e rosso qui sopra sono uguali (congruenti): i lati AE e AB sono uguali in quanto lati di uno stesso quadrato; anche AC e AH sono lati di uno stesso quadrato. Affinché due triangoli siano uguali, oltre a due lati deve essere uguale anche l'angolo compreso: e ciò è senz'altro vero per gli angoli in A dei due triangoli, in quanto sono entrambi pari all'angolo α più un angolo retto.



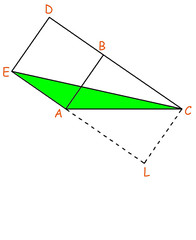
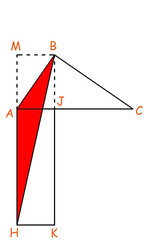
Vediamo ora l'area del triangolo verde. Se prendiamo come base il lato AE, l'altezza è la proiezione di C sul prolungamento di AE, quindi risulta essere CL. Ma CL è uguale ad AB (lati opposti di un rettangolo): base e altezza del triangolo coincidono con i lati del quadrato costruito su AB, quindi l'area di questo triangolo è metà dell'area del quadrato stesso.

Per quanto riguarda l'area del triangolo rosso, se prendiamo AH come base, l'altezza è la proiezione di B sul prolungamento di AH, quindi risulta essere BM. Dato che BM è uguale ad AJ (lati opposti di un rettangolo), il triangolo ha per base e altezza i lati del rettangolo AJKH, quindi il triangolo rosso ha area metà del rettangolo stesso.

Ricapitolando: il triangolo verde ha area metà del quadrato costruito sul cateto AB; il triangolo rosso ha area metà del rettangolo che ha per lati l'ipotenusa e la proiezione del cateto AB sull'ipotenusa stessa; ma i due triangoli sono uguali, quindi le aree del quadrato e del rettangolo sono anch'esse uguali: ecco dimostrato il cosiddetto "Primo Teorema di Euclide".



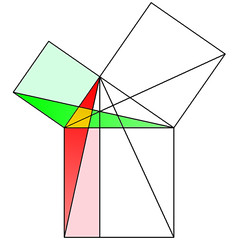
Per completare la dimostrazione del Teorema di Pitagora basta replicare il discorso per il cateto BC, il quadrato costruito su di esso e il rettangolo JCIK. Ciascuno dei quadrati costruiti sui cateti ha area uguale ai due rettangoli in cui è stato diviso il quadrato costruito sull'ipotenusa, quindi la somma dei quadrati costruiti sui cateti è equivalente al quadrato costruito sull'ipotenusa.   ▲