Euclide: il "Secondo" Teorema

Sommario:

+ Gli Elementi di Euclide
+ Euclide: Il "Primo" Teorema
– Euclide: Il "Secondo" Teorema
      Un po' di confusione?
      Elementi, Libro VI, Proposizione 8
      Geometria vs. Proporzioni

Un po' di confusione?

Così come già evidenziato a proposito del Primo Teorema, nei suoi Elementi Euclide non enuncia mai esplicitamente ciò che tradizionalmente viene indicato come suo "Secondo Teorema":

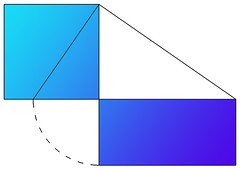
In un triangolo rettangolo, il quadrato costruito sull'altezza relativa all'ipotenusa è equivalente al rettangolo che ha per lati le proiezioni dei due cateti sull'ipotenusa".

Questo enunciato è estratto da vari teoremi, come vedremo qui di seguito.   ▲  

Elementi, Libro VI, Proposizione 8

Se in un triangolo rettangolo si conduce la perpendicolare dell'angolo retto sulla base, la stessa perpendicolare divide il triangolo in due triangoli simili e tutto quanto il triangolo e fra loro

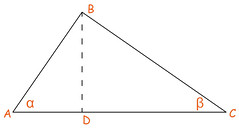
Dato il triangolo ABC, rettangolo in B, tracciamo l'altezza BD relativa all'ipotenusa. Questa divide l'ipotenusa stessa in due segmenti che sono la proiezione dei cateti, e divide il triangolo iniziale in due più piccoli ABD e BCD.

Prendiamo in esame il triangolo iniziale ABC e quello di sinistra ABD: sono entrambi rettangoli (rispettivamente in B e in D), e hanno l'angolo α in comune; di conseguenza sono uguali anche gli angoli rimanenti (in C e in B).

Discorso analogo se si prendono in esame il triangolo iniziale ABC e quello di destra BCD: sono entrambi rettangoli (rispettivamente in B e in D), e hanno l'angolo β in comune; di conseguenza sono uguali anche gli angoli rimanenti (in A e in B).

I tre triangoli hanno quindi tutti gli angoli corrispondenti uguali fra loro e dunque, per il primo criterio di similitudine dei triangoli, sono simili fra loro. (Chiaramente Euclide nei suoi Elementi non manca di dimostrare la validità di questo criterio di similitudine).   ▲  

Geometria vs. Proporzioni




L'angolo α è in comune fra il triangolo originale ABC e il triangolo di sinistra ABD, menree l'angolo β è in comune fra il triangolo originale ABC e il triangolo di destra BCD. Tutti e tre i triangoli sono rettangoli (per definizione quello originale e per costruzione i due più piccoli): allora si può applicare il "primo criterio di similitudine dei triangoli", secondo il quale

Affinché due triangoli siano simili occorre che siano uguali tutti e tre gli angoli (in realtà ne bastano due: il terzo viene di conseguenza, grazie al fatto che la somma degli angoli interni di qualsiasi triangolo è sempre 180°). Quindi vediamo: i tre triangoli sono rettangoli (quello originale in B, gli altri in D); l'angolo α è in comune fra il triangolo originale e il triangolo di sinistra; l'angolo β è in comune fra il triangolo originale e il triangolo di destra: tutti e tre i triangoli hanno quindi gli angoli uguali.

In due triangoli simili, il rapporto fra i lati corrispondenti è costante. Si può scrivere in forma di proporzione:

AD : DB = DB : DC

oppure in forma di frazioni:

AD    DB
---- = ----
DB    DC

Moltiplicando a destra e sinistra sia per DB che per DC

AD x DB x DC    DB x DB x DC
--------------------- = ---------------------
        DB                   DC

ed eliminando i termini che compaiono sia al numeratore che al denominatore otteniamo:

AD x DC = DB x DB

Quindi:

AD x DC = DB²

Ecco che il quadrato costruito sull'altezza DB del triangolo (quindi DB²) è equivalente al rettangolo che ha per lati le proiezioni dei due cateti sull'ipotenusa (AD x DC), come volevasi dimostrare. Le aree uguali sono quelle evidenziate in azzurro nell'immagine iniziale.