Ettagono (approssimato)

L'ettagono regolare non può essere inscritto in una circonferenza se non in modo approssimato. Questa semplice costruzione dà un errore di circa un decimo di grado sull'angolo al centro CÔH.



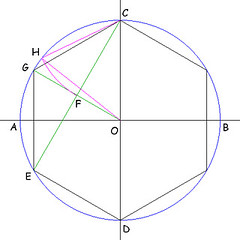
Partendo da un esagono regolare già costruito, si congiungono i punti CE e GO. Il segmento CF è l'altezza di uno dei triangoli equilateri che costituiscono l'esagono: quest'altezza è una buona approssimazione del lato dell'ettagono, che quindi basta riportare sulla circonferenza in H.

Ammettendo che la circonferenza abbia raggio unitario, il segmento CF = CH è lungo √3 / 2, infatti è l'altezza del triangolo equilatero di lato unitario. L'angolo al centro CÔH può quindi essere trovato per via trigonometrica:

CÔH = 2 asin( √3 / 4 ) = 51,3178°

mentre l'angolo teorico sarebbe

360 / 7 = 51,4286

Ecco l'animazione completa del procedimento: