Pentadecagono Regolare

La costruzione del pentadecagono regolare si basa in parte sulla costruzione del pentagono, anche se non è per niente scontato che possa essere disegnato con riga e compasso: infatti è richiesta la divisione dell'angolo al centro del pentagono in tre parti; e in generale la trisezione degli angoli non è una delle operazioni possibili con con gli strumenti della geometria classica.

Per fortuna l'angolo al centro del pentadecagono è di 24 gradi (24 x 15 = 360), e può essere facilmente ottenuto per differenza degli angoli dell'esagono e del decagono (60 - 36 = 24). Euclide, nei suoi "Elementi", fa un calcolo diverso: prende un angolo piano (180°) al quale sottrae 60° (angolo al centro dell'esagono) e 72° (angolo al centro del pentagono); ciò che rimane sono 180 - 60 - 72 =48°, di cui fa la bisezione per ottenere l'angolo di 24°. Qui di seguito invece mostro il sistema che a me sembra più semplice:



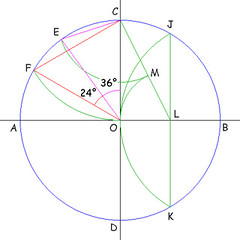
Si trova il punto medio L del raggio OB. Si traccia il segmento CL sul quale, puntando il compasso in L e con raggio LO (mezzo raggio), si trova il punto M. Il segmento CM è il lato del decagono, che riportiamo sulla circonferenza in E, quindi l'angolo CÔE è di 36°.

Puntando il compasso in C si riporta la lunghezza del raggio sulla circonferenza in F, quindi l'angolo CÔF è di 60°. La differenza fra i due angoli è 24°, cioè proprio l'angolo al centro di ciascun lato del pentadecagono.

Ecco l'animazione del procedimento: