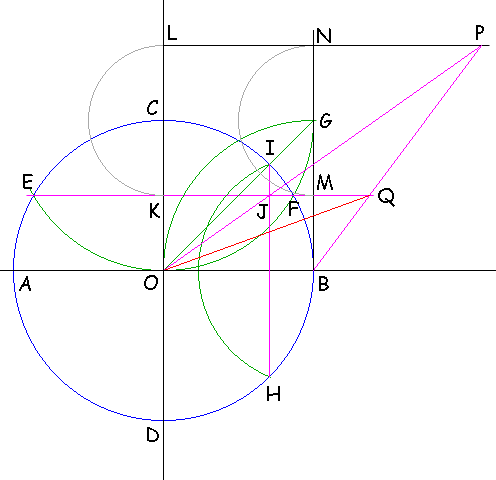
Con apertura pari al raggio OB della circonferenza, puntando il compasso in B si traccia l'arco OG, e puntandolo in C l'arco EOFG. Unendo i punti E ed F si trovano i punti K ed M. Sempre con apertura pari al raggio della circonferenza, puntando il compasso in B si traccia l'arco OG. Congiungendo O con G si trova il punto I sulla circonferenza; con apertura BI e puntando il compasso in B si traccia l'arco IH trovando il punto H. L'intersezione dei segmenti EM e IH dà il punto J.
La linea LP è parallela al diametro orizzontale, dal quale si trova alla distanza di un raggio e mezzo. Per determinarla si tracciano due archi di cerchio con apertura pari a mezzo raggio CK e puntando in C e G: si trovano rispettivamente i punti L ed N. Si uniscono i punti O e J e si prolunga il segmento fino a trovare il punto P; infine si uniscono i punti P e B trovando Q, e O con Q: l'angolo QÔB è di 20° con un errore inferiore al millesimo di grado.
L'angolo trovato è metà dell'angolo al centro dell'ennagono, proprio l'angolo necessario per completare la costruzione (vedi animazione qui sotto).
Ammettendo che il cerchio abbia raggio unitario e il suo centro sia alle coordinate 0, 0 (origine del piano cartesiano), il punto J si trova alle coordinate √2 / 2, 1/2. Per costruzione geometrica il segmento JQ è 2/3 del raggio OB, quindi le coordinate del punto Q sono √2 / 2 + 2/3, 1/2. A questo punto si può determinare l'angolo QÔB per via trigonometrica:
QÔB = atan( 1/2 / ( √2 / 2 + 2/3 ) ) = 19,99953°
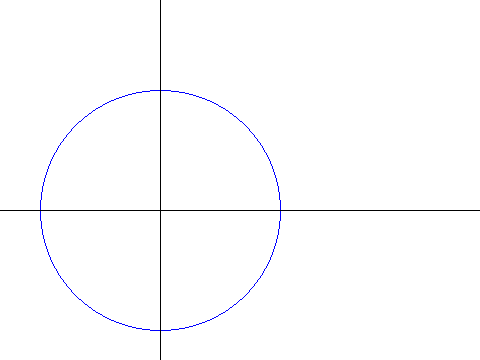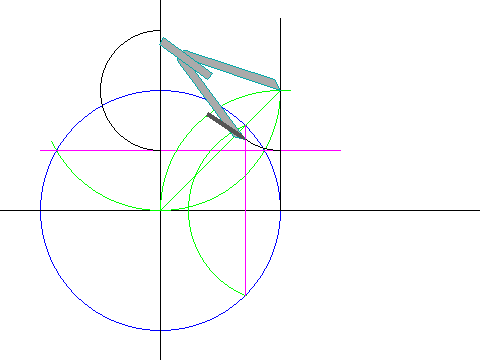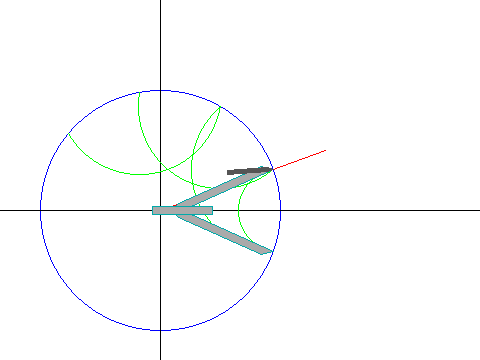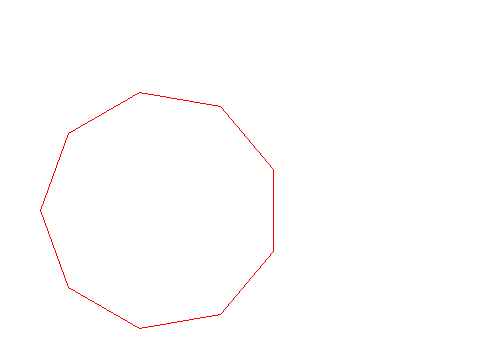
Ecco l'animazione del procedimento:
Nessun commento:
Posta un commento