Ottica: Interferenza

Sommario:

+ Introduzione
+ Riflessione
+ Rifrazione
+ Diffrazione
+ Cannocchiale e Aberrazione sferica
+ Dispersione e Telesopio di Newton
+ Etere Luminifero
+ Birifrangenza e Polarizzazione
– Interferenza
      Una strana grandinata
      Uno strano specchio di mare
      Thomas Young
      Esperimento della doppia fenditura
      Leggi di Fresnel
      Dettagli sulla simulazione della grandine
+ L'arcobaleno

Una strana grandinata

L'altro giorno sono dovuto uscire di casa mentre il tempo prometteva un bel temporale... e io avevo un buco nel tetto. Per non rischiare danni maggiori, ho sistemato un bel catino proprio sotto al buco; ma quando sono tornato la situazione era questa:



C'era stata una grandinata eccezionale, e io ho trovato sì il catino pieno di ghiaccio, ma molti chicchi erano sparsi sul pavimento. Una spiegazione potrebbe essere che il catino si sia riempito troppo, o che qualche chicco ne sia rimbalzato fuori; nonostante queste ipotesi, ho voluto appurare se per caso non succeda qualcosa durante il viaggio: siamo sicuri che tutti i chicchi di grandine arrivino sempre nel catino?



Nell'animazione qui sopra mostro 4 casi diversi:

A      — il chicco di grandine cade lontano dal buco, quindi non arriverà mai sul mio pavimento.
B      — il chicco passa esattamente dal centro del buco, e infatti cade nel catino.
C, D — questi due chicchi di grandine rimbalzano sul bordo del buco, deviano la loro traiettoria e cadono sul pavimento.

Nuova curiosità: quante probabilità ci sono che i chicchi di grandine cadano fuori dal catino?

Con una simulazione al computer ho fatto cadere i chicchi di grandine da posizioni casuali, registrando per ciascuno il punto di arrivo sul pavimento. Accumulando un milione di prove ho potuto costruire il grafico che segue: l'altezza variabile del grafico bianco a forma di campana indica la quantità di chicchi che è caduta in ogni punto del pavimento.



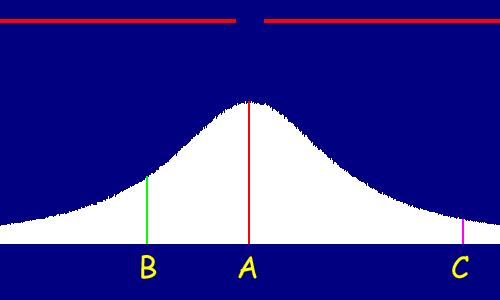
Il punto indicato con A sul pavimento è proprio sotto al buco nel tetto, e la linea rossa, che indica l'altezza della campana in quel punto, dimostra che le probabilità che un chicco di grandine cada proprio lì sono massime. Il punto B è in una zona che non si trova sotto al buco, eppure le probabilità che i chicchi di grandine cadano lì (indicate dalla lunghezza della linea verde) sono tutt'altro che trascurabili. Infine il punto C, molto lontano dal buco, ha anch'esso una buona probabilità di essere raggiunto dalla grandine!


Ieri ho scoperto di avere un secondo buco nel tetto, e stava arrivando un altro temporale. Certo non speravo più di potermela cavare sistemando un semplice paio di catini, in compenso mi è venuta un'altra curiosità: ora che ci sono due buchi, quali sono le probabilità che i chicchi di grandine cadano nei vari punti del pavimento?



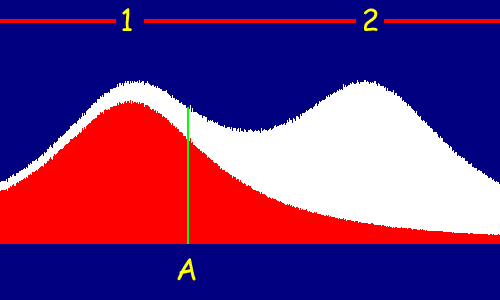
Le cifre 1 e 2 indicano i due buchi nel tetto. La riga verde sopra al punto A indica le probabilità totali che i chicchi di grandine cadano sul pavimento proprio in quel punto: l'area in rosso infatti indica le probabilità che hanno di arrivare nei vari punti del pavimento i chicchi che passano dal buco 1, mentre l'area in bianco si riferisce ai chicchi di grandine che passano dal buco 2; la somma di queste due curve di probabilità dice quanto ghiaccio cadrà su ogni punto del pavimento.   ▲  

Uno strano specchio di mare

Dopo aver ripulito tutto (e tappato i buchi nel tetto), per rilassarmi sono andato al mare. Come per incanto i miei pensieri hanno abbandonato la grandine... per occuparsi delle onde marine: infatti mi è capitato di vedere dal vivo il fenomeno di diffrazione di cui abbiamo già parlato qui. Mi sono chiesto come variasse l'altezza dell'acqua momento per momento, e ho ottenuto quanto segue:



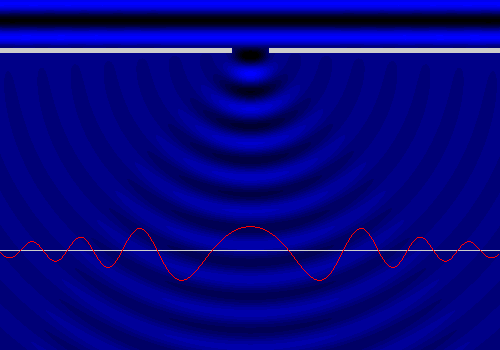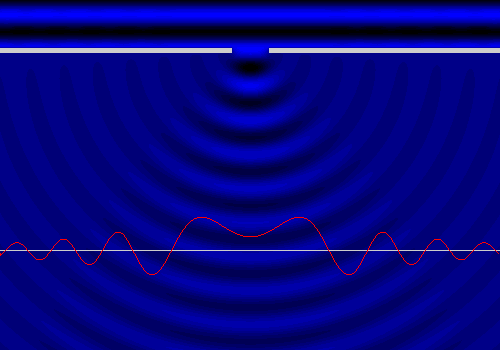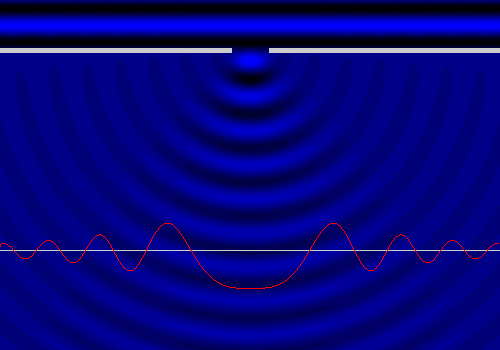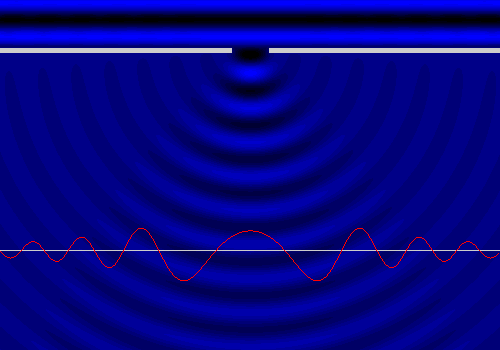
La linea rossa indica in ogni istante l'altezza dell'acqua che si trova in corrispondenza della linea grigia. Ciò che però mi interessa in modo particolare è l'ampiezza delle onde, non l'altezza istantanea dell'acqua: nel disegno che segue, il grafico rosso indica l'altezza massima raggiunta dall'acqua in ogni punto, e quindi l'ampiezza delle relative onde.



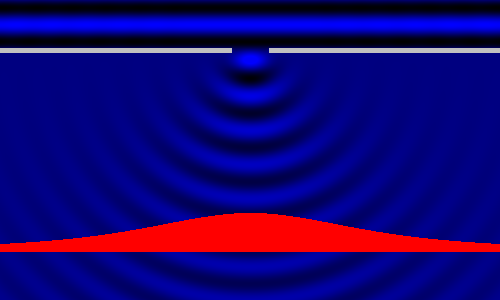
Mi sono stupito nel vedere la netta somiglianza fra il comportamento di queste onde e quello della grandine che abbiamo visto prima. Nell'immagine qui sotto, a sinistra mi sono limitato ad "appiattire" un po' la campana della grandine: la somiglianza è davvero notevole!



Voglio ricordare che, per quanto i grafici relativi sia alla grandine che alle onde siano ottenuti grazie simulazioni fatte al computer, i procedimenti di calcolo (che riproducono la realtà dei fenomeni fisici) sono totalmente diversi: per la grandine si tratta di una statistica di eventi casuali governati dalle leggi della meccanica, mentre per le onde si tratta della simulazione di una matrice di punti materiali legati da molle, come spiegato qui. Proprio il fatto che i risultati siano così simili spiega perché è stato così difficile capire di cosa fosse fatta la luce, se onde o corpuscoli!

Proseguendo nella mia passeggiata sul lungomare mi sono imbattuto in un altro fenomeno: onde che passano contemporaneamente da due fessure diverse.



Inizialmente le onde si comportano normalmente, ma quando si diffondono fino al punto da sovrapporsi si genera un'interferenza fra i due gruppi di onde: il risultato si vede particolarmente bene nel fotogramma finale dell'animazione qui sopra.

Nell'immagine che segue possiamo vedere l'ampiezza delle onde, così come abbiamo fatto per le onde che venivano generate da una fessura unica:



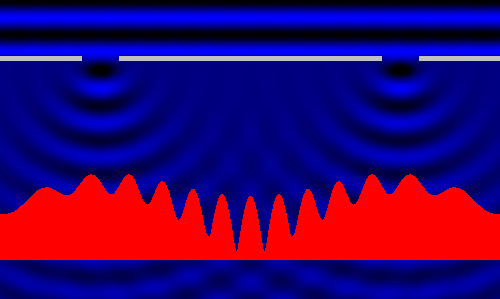
Confrontiamo quest'ultima curva con quella della grandine che passa attraverso due buchi:



Si vede subito che c'è una differenza notevolissima: la curva di sinistra (grandine) ha un andamento dolce, molto continuo; quella di destra presenta un andamento di massima (indicato dalla linea gialla) molto simile, ma esibisce anche delle rapide oscillazioni, dei massimi e dei minimi molto sfrangiati: infatti questo genere di curva, riferito ai fenomeni ondulatori, si chiama proprio "Frangia di interferenza".

A cosa si devono le frange d'interferenza? Le onde generate in corrispondenza delle due fessure hanno la stessa ampiezza e partono con la stessa fase (ossia, si trovano sempre al loro picco massimo nello stesso istante). Le onde però ci mettono del tempo per diffondersi, e ciò genera "sfasamenti" variabili fra le onde:



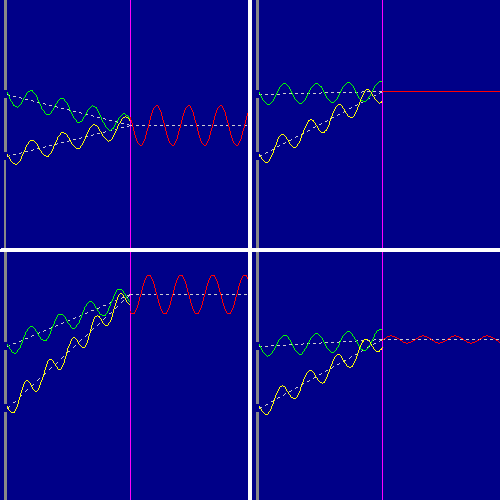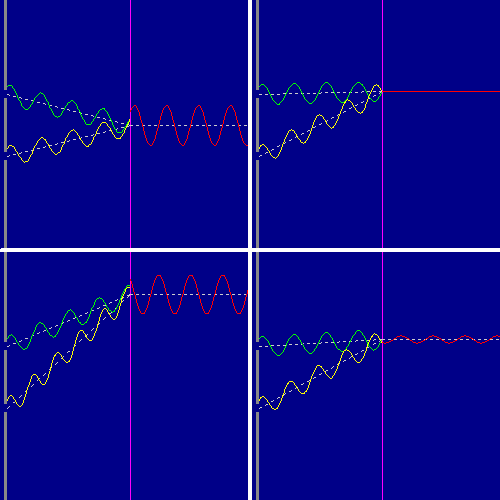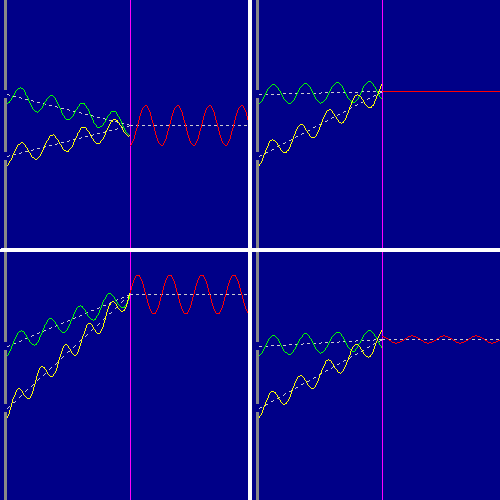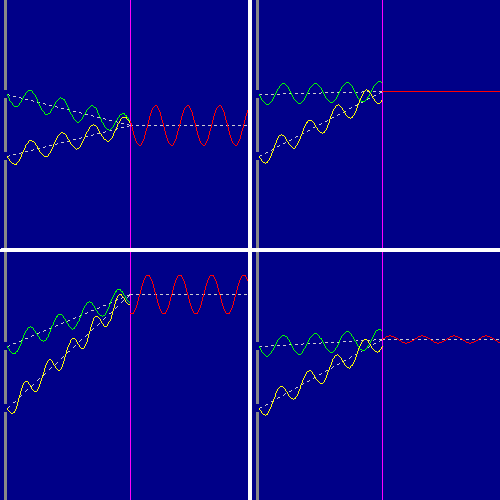
1 — In alto a sinistra si vedono due onde che impiegano esattamente lo stesso tempo per raggiungere il punto di intersezione sulla linea viola. In quel punto le onde arrivano esattamente in fase, i loro picchi coincidono sempre, quindi il loro effetto si somma; l'onda rossa ottenuta dall'unione delle due onde ha ampiezza doppia rispetto a ciascuna delle onde verde e gialla.

2 — In alto a destra la lunghezza del cammino compiuto dalle due onde differisce per esattamente mezza lunghezza d'onda. Questo vuol dire che quando una si trova al picco massimo, l'altra è al picco opposto: praticamente c'è una continua compensazione pieno-vuoto, e l'onda generata ha ampiezza nulla.

3 — In basso a sinistra le due onde arrivano nuovamente in fase, ma data la differente lunghezza dei cammini percorsi, l'onda gialla compie un'oscillazione in più rispetto a quella verde. Il risultato è un'onda di ampiezza pari a quella generata nel caso 1.

4 — In basso a destra la confluenza fra le due onde si verifica in un punto in cui sono quasi in controfase, cioè i picchi positivo e negativo si compensano ma senza annullarsi del tutto: l'onda che ne esce ha un'ampiezza molto ridotta.

Nota: tutti i punti di confluenza delle onde che partono dalle fessure sono allineati sulla stessa linea viola; è proprio con questo tipo di procedimento che si calcolano le frange d'interferenza.

Ricapitolando, possiamo dire che onde e particelle esibiscono molti comportamenti similari; ma non l'interferenza.   ▲  

Thomas Young

Nella storia dell'ottica ci siamo già imbattuti in vari personaggi notevoli, come Fermat, Huygens, Newton. Quello che vi presento ora, per certi versi, è forse il più incredibile di tutti: ecco a voi... Thomas Young!



Nasce nel 1773 in Inghilterra. A due anni sa leggere e scrivere; a sei conosce già il latino, a quattordici anche greco, francese, italiano, ebraico, caldeo, siriaco, samaritano, arabo, persiano, turco ed etiope!

Nel 1792 inizia il corso di studi in medicina a Cambridge, infatti agli inizi del XIX secolo Young è (almeno in teoria) un medico: ma è molto più interessato alle malattie, che ai malati. Per fortuna un vecchio zio vede bene di lasciargli una ricca eredità, per cui gradualmente lascerà ad altri la cura dei pazienti per dedicarsi liberamente ai suoi studi.

Le sue ricerche spaziano in moltissimi campi: porta il nome di "modulo di Young" un coefficiente usato nello studio della deformazione dei materiali; compie importanti studi riguardo la capillarità e la tensione superficiale dei liquidi; in particolare è il primo ad usare il termine energia nel senso che gli diamo oggi, ma... non avevamo detto che era un medico? Beh, in effetti si era laureato anche in fisica a Gottinga, chissà se per l'occasione avrà imparato anche il tedesco!

A proposito di medicina, e in particolare di fisiologia, già nel 1793 riesce a spiegare, a seguito di esperimenti originali da lui compiuti, che la messa a fuoco nell'occhio dipende dalla variazione di curvatura della superficie interna del cristallino. Nel 1801 pubblica le sue ricerche secondo le quali l'elemento sensibile dell'occhio sarebbe la retina, non il cristallino come molti credevano; inoltre che la percezione dei colori sarebbe dovuta a "solo" tre tipi diversi di terminazioni nervose sensibili al rosso, al verde e al blu... e tutto questo, ancora prima di aver compiuto trent'anni.

In quegli stessi anni si occupa anche di ricerche sulla luce... ma prima devo spiegare cosa ci stia a fare qui sopra, assieme al suo ritratto, quel testo scritto in caratteri antichi: si tratta di una sezione della celeberrima Stele di Rosetta, la pietra "trilingue" che ha consentito di decifrare, dopo enormi sforzi, le due scritture egizie (geroglifico e demotico) a partire da un testo greco (il greco non compare nella foto).

Ebbene, il primo a capirci qualcosa... fu proprio il nostro Thomas Young, contribuendo alla fondamentale scoperta che si tratta di due scritture basate su fonogrammi (a ogni segno corrisponde un suono, come negli alfabeti moderni), invece che su semagrammi (a ogni simbolo corrisponde un concetto), come ritenuto da tutti coloro che avevano studiato le scritture egizie fino ad allora.

Per finire con gli aneddoti biografici: nel suo articolo "Lingue", scritto per la Encyclopaedia Britannica, Young mette a confronto grammatica e vocabolario di QUATTROCENTO lingue... ebbene sì, credo proprio che il tedesco lo avesse imparato!   ▲  

Esperimento della doppia fenditura

Nel corso dei suoi studi sulla fisiologia dell'occhio, Young non può non interrogarsi sulla natura della luce, e va convincendosi che si tratti di un fenomeno ondulatorio. Evidentemente conosce bene il fenomeno dell'interferenza, infatti prova a verificare se anche la luce produca fenomeni di interferenza.

Per quanto la luce abbia una lunghezza d'onda piccolissima (inferiore al millesimo di millimetro), e quindi apparentemente sia molto difficile da maneggiare, l'esperimento è più facile da realizzare di quanto sembri. Infatti l'interferenza delle onde ha la proprietà per cui, allontanandosi dalla doppia fenditura, le zone di rafforzamento o di elisione delle onde diventano sempre più ampie; le linee nella figura che segue sono tracciate in corrispondenza dei punti sui quali non si generano onde:



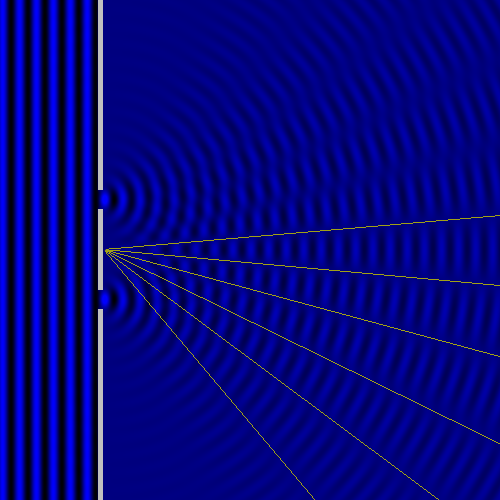
Ho provato a realizzare l'esperimento per conto mio usando un piccolo puntatore laser (ATTENZIONE: se decideste di replicare l'esperimento, non dirigete mai la luce del puntatore direttamente negli occhi, né vostri né altrui):



In alto a sinistra si vede un cartoncino che funge da schermo, che ha due piccolissimi fori praticati mediante uno spillo. Il puntatore laser illumina i due fori per proiettare un doppio fascio di luce su un foglio a quadretti posizionato a circa cinque metri di distanza (anche se non si vedono bene, i quadretti hanno più o meno le stesse dimensioni in tutti e quattro gli scatti). Ecco i risultati dell'esperimento:

— In alto a destra si vede la proiezione del raggio laser così com'è, senza schermo interposto.

— In basso a sinistra si vede la proiezione del raggio laser che passa attraverso uno solo dei fori nel cartoncino: il disco di luce è più ampio ma ha un'intensità ridotta, ed intorno ad esso è visibile qualche anello di diffrazione.

— In basso a destra il raggio laser passa attraverso i due forellini: si vede comparire chiaramente la frangia d'interferenza. Insomma: è proprio vero che nelle condizioni giuste luce più luce fa buio!

Ovviamente Young non dispone di un raggio laser, ma riesce a notare qualcosa di sorprendente anche con la semplice luce solare. La quale, come sappiamo, è una mescolanza di colori, ciascuno associato ad una diversa lunghezza d'onda: Young infatti non vede zone di chiaro-scuro (quelle si vedono solo con una sorgente di luce monocromatica), ma frange variamente colorate.

Nel 1802 pubblica sulle Philosophical Transactions della Royal Society un articolo dal titolo "Resoconto di alcuni casi di produzione dei colori non ancora descritti" in cui descrive questa e altre esperienze, che spiega in base alla teoria ondulatoria. Ma nell'immediato questo suo articolo non ottiene grandi riconoscimenti: da un lato è scritto in modo non molto chiaro, utilizzando un approccio matematico piuttosto elementare (quindi viene un po' snobbato dagli altri scienziati); ma soprattutto...

... Young si macchia del delitto di "lesa maestà"! Infatti sostenendo la teoria ondulatoria della luce va contro l'opinione di Newton, e questa è una cosa che il mondo scientifico inglese non può assolutamente tollerare, soprattutto se a farlo è proprio un inglese!   ▲  

Leggi di Fresnel

Il testimone quindi "attraversa" la Manica... e viene preso in consegna dai francesi, come il Malus di cui abbiamo parlato a proposito della polarizzazione. Il personaggio più importante in questa fase fu Augustin-Jean Fresnel (quello delle "lenti di Fresnel", 1788-1827): nel corso di molti anni elabora le formule che spiegano tutti i fenomeni di riflessione, rifrazione, interferenza, diffrazione. lo studio della luce polarizzata lo porta dopo molte incertezze ad accettare una luce composta di onde trasversali, sostenendo l'ipotesi più difficile da digerire per quanto riguarda la propagazione della luce.

Infatti quando Fresnel presenta i suoi studi all'Accademia delle Scienze di Parigi, tra il 1815 ed il 1819, suscita le immediate proteste di personaggi del calibro di Pierre Simon Laplace e di Siméon-Denis Poisson, sostenitori della teoria corpuscolare.

In particolare Poisson studia i lavori di Fresnel nella speranza di trovarci qualche punto debole, e a un certo punto è sicuro di averlo trovato: secondo le formule di Fresnel, se un fascio di luce investe uno schermo circolare, al di là dell'ostacolo, lungo l'asse che congiunge la sorgente di luce e il centro dello schermo, dovrebbe comparire un raggio di luce; il che secondo Poisson evidentemente è impossibile.



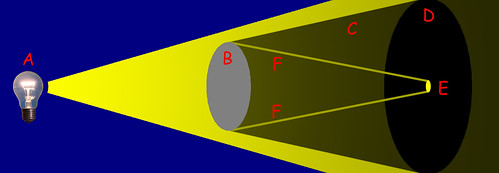
La verifica viene fatta immediatamente, e il risultato è che questo raggio di luce si "materializza" davvero! La spiegazione sta nel fatto che al momento che la luce generata in A raggiunge lo schermo B, dal bordo di B si irradiano le onde che generano i normali fenomeni di diffrazione. Quindi tutti i punti che si trovano lungo l'asse che si prolunga oltre il centro dello schermo saranno equidistanti dal bordo dello schermo stesso, e riceveranno le onde diffratte perfettamente in fase, sommandosi.

Ho realizzato una simulazione di questo fenomeno, modificando il mio programma delle onde in modo da fare i calcoli su una matrice a tre dimensioni. Dopo circa sei ore di calcoli, il computer ha fornito questo risultato:



In realtà questo fenomeno era già stato descritto nel 1723 da Giacomo Filippo Maraldi (1665-1729), ma la sua osservazione fu per lo più ignorata, fino ad essere riscoperta nell'occasioe che ho raccontato più sopra. Per ironia della sorte, oggi questo fenomeno è noto come "Macchia di Poisson".

In compenso prende il nome di "Diffrazione di Fresnel" il fenomeno complementare: se invece di investire un ostacolo circolare il fascio di luce viene fatto passare in mezzo ad un'apertura rotonda, poco al di là dell'apertura si viene a creare un "punto nero", una zona in cui la luce proveniente direttamente dalla sorgente luminosa e le onde diffratte dal bordo dello schermo si elidono completamente. Ecco qui un'altra simulazione (altre sei ore di calcolo per il mio povero computer); il "punto nero" è evidenziato dal rettangolo rosso alla fine dell'animazione:



Con questa storia abbiamo assistito a uno dei casi più straordinari di applicazione del "metodo scientifico": una massa di indizi (i fenomeni della luce), che consentono di elaborare leggi matematiche (le leggi di Fresnel), che consentono di prevedere un fenomeno mai osservato prima (la macchia di Poisson), che supera la prova sperimentale: a me sembra una cosa davvero straordinaria! E anche Fresnel doveva essere dello stesso parere, infatti scrive:

Tutti i complimenti che ho ricevuto [...] non mi hanno mai fatto così tanto piacere come la scoperta di una verità teoretica, o la conferma di un calcolo dall'esperimento

  ▲  

Dettagli sulla simulazione della grandine

Tutti i testi che si occupano di interferenza fanno il confronto fra il comportamento delle particelle o delle onde che passano attraverso buchi o fessure, ma molto spesso sostituiscono alla parola "particelle" la parola "proiettili".

Inizialmente pensavo di parlare anch'io di proiettili, poi mi è venuto in mente che la grandine poteva essere un miglior espediente narrativo. La sostanza comunque non cambiava.

La faccenda del proiettile (o grandine) mi ha portato fuori strada nello scrivere il programma di simulazione, per almeno due ordini di motivi: il primo è che il buco nel tetto deve avere esattamente lo stesso diametro dei chicchi di grandine.



Infatti provando con un buco più grande, le probabilità che i chicchi passino in mezzo al buco, senza toccarne il bordo, sono nettamente superiori a qualsiasi altro percorso che comprenda un urto con il bordo stesso. Con un buco più grande il risultato sarebbe questo:



Il secondo problema riguarda il calcolo dell'angolo di deviazione del chicco di grandine dopo l'urto. Infatti ho scritto un programma che riproduceva le normali leggi fisiche relative agli urti elastici fra corpi rigidi:



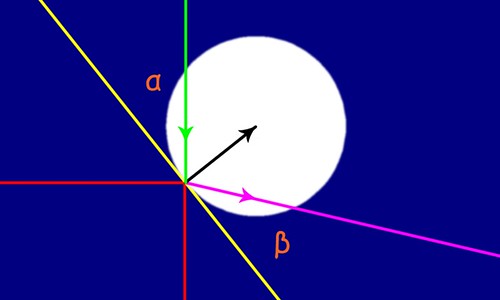
Il chicco di grandine scende in direzione verticale, e un punto della sua circonferenza (il cui moto è indicato dalla freccia verde) colliderà con lo spigolo del buco nel tetto (linee rosse). Al momento dell'urto il chicco riceve una spinta orientata secondo il raggio indicato in nero (è il raggio che congiunge il punto di impatto con il centro del chicco), e in pratica è come se avvenisse un rimbalzo del chicco sulla linea gialla, perpendicolare al raggio nero. Come conseguenza dell'urto, la traiettoria del chicco di grandine viene deviato in modo che l'angolo β sia uguale all'angolo α.

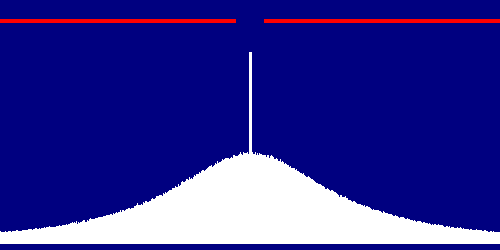
Eseguendo il programma di simulazione mi sono sorpreso molto nel vedere risultati come questo:



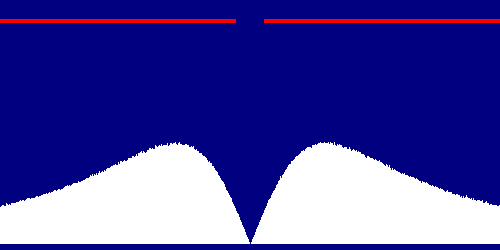
Le sezioni laterali della curva sono molto simili a quelle che abbiamo visto sopra, nella spiegazione dell'interferenza; ma guardando la zona centrale salta fuori che le probabilità di trovare chicchi di grandine proprio sotto al buco nel tetto sono praticamente nulle!

Questo è un fenomeno che mi sarei dovuto aspettare... invece ho perso diverse ore a cercare il "baco" nel programma. L'origine di questo inaspettato comportamento dei chicchi di grandine può essere compreso con lo schema che segue:



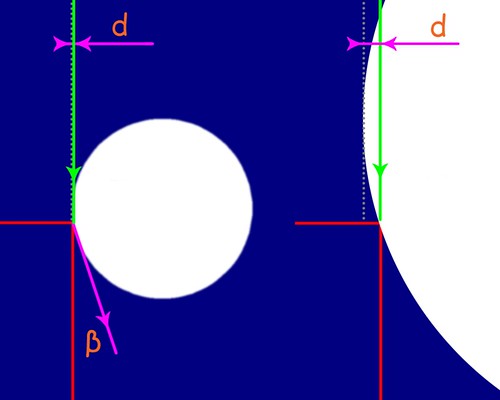
Affinché l'angolo β sia molto stretto, la distanza orizzontale d fra il margine sinistro del chicco e il bordo dello spigolo (vedi anche l'ingrandimento sulla destra) deve essere ridottissima; quindi le probabilità che il chicco di grandine sfiori il bordo del buco così di striscio da non essere quasi deviato nella sua traiettoria sono praticamente nulle: per chi mastica un po' di trigonometria, il problema risiede nell'elevatissima sensibilità della funzione arcoseno per angoli vicini ai 90°.


Alla fine ho optato per un altro genere di simulazione: non un urto elastico fra due corpi rigidi, ma una repulsione di tipo "quadratico inverso", analoga a quella che si ha fra cariche elettriche o poli magnetici dello stesso segno.



Durante la sua caduta, l'oggetto c viene respinto da entrambi i poli a e b che sono idealmente posizionati ai lati del buco nel tetto. Le forze dipendono dall'inverso del quadrato delle distanze: siccome la distanza ac è minore della bc, l'oggetto c è spinto a destra dal polo a più di quanto lo sia verso sinistra dal polo b, quindi devia verso destra (freccia viola).

I risultati ottenuti, come quelli che ho mostrato parlando dell'interferenza, sono esattamente quelli che si vedono nei testi scientifici. Le mie simulazioni non rispecchiano quindi il comportamento della grandine, che come dicevo è stata scelta come espediente narrativo per rendere facilmente comprensibili i fenomeni; d'altra parte il metodo di calcolo che ho adottato rispecchia fedelmente il comportamento di altri fenomeni fisici, maggiormente appropriati allo studio dell'interferenza, ma che sarebbero stati più complicati da descrivere.   ▲  

Prossimo capitolo: L'arcobaleno