Ottica: Rifrazione

Sommario:

+ Introduzione
+ Riflessione
– Rifrazione
      Ricerca della legge degli angoli
      Cartesio e Fermat: una celebre controversia
      Il "principio del Minor Tempo"
+ Diffrazione
+ Aberrazione sferica e Cannocchiale
+ Dispersione e telescopio di Newton
+ Etere Luminifero
+ Birifrangenza e Polarizzazione
+ Interferenza
+ L'arcobaleno

Rifrazione

Nell'immagine che segue è fotografato un cucchiaino immerso in un recipiente di vetro contenente acqua. Com'è che invece di un cucchiaino se ne vedono tre?



I pallini rossi indicano: con A la parte del cucchiaino fuori dall'acqua; con B e C due immagini della parte immersa, infine con D un'ulteriore immagine della parte immersa, addirittura capovolta! Domanda: fra B, C e D, quale immagine rappresenta il vero cucchiaino?

In realtà... nessuna delle tre! Vediamo i percorsi ottici della luce che dal cucchiaino raggiungono l'osservatore. Per cominciare a studiare il problema, vediamo cosa succederebbe se il contenitore fosse vuoto:

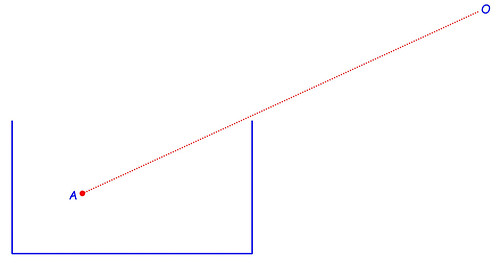
Il pallino rosso contrassegnato con A rappresenta il cucchiaino mentre, a destra in alto, il punto O rappresenta l'occhio dell'osservatore. La linea punteggiata rossa è un segmento rettilineo che congiunge A con O: in mancanza di acqua nel recipiente, si vedrebbe un'unica immagine, proprio in quella direzione. Adesso versiamo l'acqua nel contenitore:


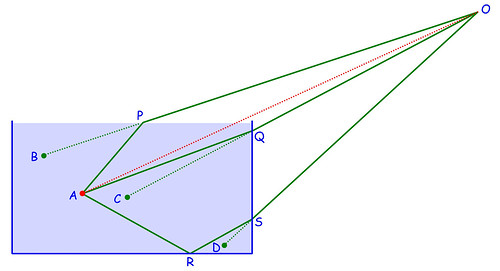
Di nuovo, Il "vero" cucchiaino è rappresentato dal pallino rosso indicato dalla lettera A, mentre O rappresenta l'occhio dell'osservatore. In presenza di acqua nessun raggio di luce percorre il segmento rettilineo da A ad O; infatti tutte le volte che la luce attraversa una superficie di separazione fra mezzi diversi (in questo caso, aria e acqua) devia la propria traiettoria:

— Primo percorso: la luce si propaga da A verso l'alto; per il fenomeno della rifrazione devia in P raggiungendo l'osservatore secondo la direzione P-O, e questo dà all'osservatore stesso l'impressione che una "copia" dell'oggetto A sia visibile nel (ovvero in direzione del) punto B.

— Secondo percorso: la luce si propaga da A verso destra, devia in Q e raggiunge l'osservatore secondo la direzione Q-O: ecco quindi l'impressione di una seconda copia dell'oggetto A, visibile nella posizione C.

— Terzo percorso: la luce si propaga verso il fondo del contenitore riflettendo in R per poi raggiungere la parete del contenitore in S; a seguito della rifrazione, la luce devia e raggiunge l'osservatore secondo la direzione S-O: ecco la terza copia di A visibile nel punto D. Nota: il fatto che in questo processo ci sia stata una riflessione, giustifica il fatto che, nella fotografia in alto, la copia D del cucchiaino risulti capovolta.

Ricapitolando, il cucchiaino riceve luce dall'ambiente e la riflette in tutte le direzioni. Di tutte le direzioni possibili, quelle che dopo un qualche fenomeno di rifrazione e/o riflessione raggiungono l'occhio dell'osservatore sono ben tre; ma nessuno dei percorsi cucchiaino-occhio è rettilineo!

È ovvio a questo punto che il principio del minimo percorso di Erone non è sempre valido: è corretto per quanto riguarda la propagazione in un mezzo omogeneo e nella riflessione, ma non per quanto riguarda la rifrazione, ovvero il fenomeno che si ha quando la luce attraversa la linea di separazione fra due materiali diversi. Esisterà allora una legge che tenga conto anche di questo nuovo fenomeno?   ▲  

Ricerca della legge degli angoli

La ricerca di una legge matematica in grado di descrivere il fenomeno della rifrazione è andata avanti per molti secoli. Documentata per la prima volta in un testo scritto intorno al 984 dal matematico arabo Ibn Sahl, che la usò per ottenere i profili delle lenti asferiche (in grado cioè di ridurre le aberrazioni geometriche!), in occidente fu scoperta da Thomas Harriot nel 1602, che però non la pubblicò. Finalmente nel 1621 fu trovata ancora una volta da Willebrord Snell (matematico, astronomo e fisico olandese, 1580-1626): oggi è effettivamente nota come "Legge di Snell".

Per ottenere una legge matematica bisogna avere una serie di dati sperimentali: come si fa a ricavarli? Con uno schema come il seguente:


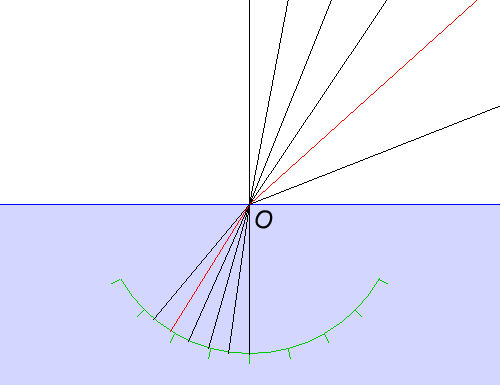
Si proietta sul punto O della superficie dell'acqua un raggio di luce secondo un angolo di incidenza noto. Centrato in O c'è un goniometro (indicato in verde) grazie al quale si legge il punto di arrivo della luce, quindi l'angolo di rifrangenza. In base a dati raccolti in questo modo, tutti gli studiosi citati sopra sono arrivati alla seguente legge matematica:


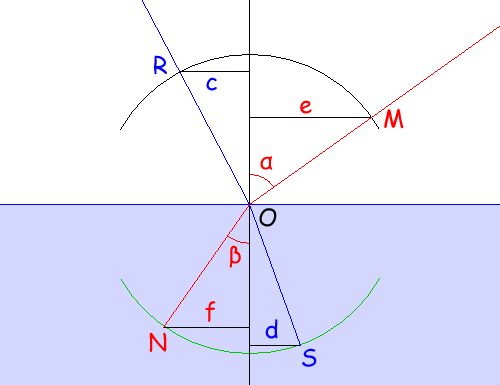
Detto α l'angolo di incidenza e β l'angolo di rifrangenza, gli angoli non sono uguali (come accade per la riflessione), né proporzionali fra loro. Ciò che rimane costante è il rapporto o proporzione fra i seni degli angoli. Per vederlo in modo più immediato, senza inoltrarci nella trigonometria, si può vedere questa regola in un altro modo: se sopra al livello dell'acqua sistemiamo un altro goniometro (indicato in nero) dello stesso raggio e con lo stesso centro di quello sotto il livello dell'acqua (verde), il rapporto fra le lunghezze c / d, oppure e / f, rimane sempre costante; e questa costante dipende dai due mezzi attraversati dalla luce: in questo caso aria e acqua, ma potrebbe essere olio e vetro... insomma una coppia qualsiasi di materiali trasparenti.   ▲  

Cartesio e Fermat: una celebre controversia

Trovata la formula, rimane la curiosità da sapere il perché di questa legge, ovvero del principio che si trova alla base di questa legge fisica. A questo proposito racconterò un episodio piuttosto interessante di storia della scienza, che vede protagonisti questi tre signori:



— René Descartes (in arte Cartesio, a sinistra): filosofo e matematico francese (1596-1650). Noto per la celeberrima frase "Cogito ergo sum" (penso dunque sono), e per l'invenzione delle "coordinate cartesiane". Molto modestamente avrebbe voluto che i suoi scritti sostituissero quelli di Aristotele nell'insegnamento universitario dell'epoca... e per questo si occupò molto approfonditamente di filosofia, teologia, e tante altre belle cose.

— Pierre de Fermat (1601-1665, al centro). Magistrato di mestiere, matematico per diletto (!): ci ha lasciato un'eredità scientifica di tutto rispetto. Noto soprattutto per il suo Ultimo Teorema, ha dato importantissimi contributi alla "teoria dei numeri", quella che ha portato all'invenzione dell'ingegnoso metodo di crittografia che si usa in internet. Scoprì i principi fondamentali della geometria analitica indipendentemente da Cartesio, arrivando a risultati straordinari, precursori del calcolo differenziale: insomma, un gigante della matematica!

— Marin Mersenne (1588-1648, a destra), teologo, filosofo e matematico francese. Noto ai matematici per i "Numeri di Mersenne" (la "sorgente" dei più grandi numeri primi trovati finora), il suo valore storico è stato di mantenere una fitta corrispondenza con tutti i più importanti studiosi dell'epoca; la pubblicazione del suo carteggio ha richiesto la stampa di ben 16 volumi, che permettono di ricostruire in dettaglio la storia del pensiero scientifico della sua epoca.

La storia inizia con Cartesio che, nella sua opera intitolata "La Dioptrique" (La Diottrica), si pone il problema della rifrazione dandone una spiegazione meccanica assolutamente stravagante, ma che in un certo senso dà risultati corretti, ovvero proprio la legge di Snell.

Cartesio scompone il moto della luce in due componenti, una parallela alla superficie di rifrazione e l'altra perpendicolare (la cosa non solo si può fare da un punto di vista matematico, ma è una pratica comunissima nello studio della fisica). Poi stabilisce due criteri fondamentali, non suffragati da nessuna prova:

— la luce si muove all'interno di ogni materiale a una velocità costante ben determinata, dipendente solo dal materiale stesso (e questo è corretto);

— quando la luce passa da un materiale a un altro, la componente "orizzontale" della sua velocità, cioè quella parallela alla superficie, non cambia; cambia invece, nel senso dell'accelerazione o del rallentamento, solo la velocità della componente verticale.


Il pensiero di Cartesio è il seguente: un raggio di luce procede con velocità V1, che viene scomposta nelle componenti Y1 (verticale) e X (orizzontale). Nell'attraversare la superficie di separazione aria-acqua, la componente orizzontale rimane invariata, mentre quella verticale cambia e diventa Y2. Con un po' di ragionamenti non molto complessi Cartesio arriva proprio alla formula di Snell, in cui il coefficiente di rifrazione n assume il significato di rapporto fra le velocità alle quali si propaga la luce nei due materiali:

sen α     v2
-------- = ---- = n
sen β     v1

in cui α e β sono gli angoli di incidenza e di rifrangenza, v1 e v2 le velocità nell'aria e nell'acqua, n appunto il coefficiente di rifrazione di Snell.

Cartesio inviò questo scritto a Mersenne per ottenere dal re di Francia il "privilegio per la stampa", e questi lo fece pervenire a Fermat. Il quale trova subito da ridire sul fatto delle velocità, e scrive a Mersenne:

... dopo aver attentamente esaminato la proposizione che è alla base della sua Dioptrique e che stabilisce il rapporto di rifrazione, divenni sospettoso sulla sua prova dato che la sua dimostrazione mi appariva come un vero paralogismo [...] poiché egli suppone poi che il moto della luce in aria e nei corpi rarefatti è più difficile, o se voi preferite, più lento del moto nell'acqua e negli altri corpi densi, il che mi sembra offenda il senso comune; infine poiché egli afferma che una delle direzioni o delle determinazioni del moto di una palla sussiste interamente dopo aver incontrato il secondo mezzo...

Relativamente alle velocità, Fermat fa un'osservazione appropriata: guardando i grafici che ho mostrato più sopra, si vede che l'angolo di rifrazione nell'acqua è sempre più "stretto" di quello di incidenza; quindi, a parità di velocità in senso orizzontale, la velocità in senso verticale deve aumentare passando dall'aria all'acqua.

C'è da dire che a me non sembra del tutto inverosimile che qualcuno trovasse logica una velocità di propagazione della luce maggiore nell'acqua che nell'aria... per fare un esempio, è noto che il suono si propaga nell'acqua più velocemente che nell'aria, e nell'acciaio più velocemente ancora! Proprio a questo proposito Cartesio si esprime così:

Smetterete, comunque, di trovarlo un effetto strano, ricordando la natura da me attribuita alla luce, quando dissi che non è altro che un certo moto o un'azione concepita in una materia molto sottile [*], che riempie i pori di tutti gli altri corpi e considerando che, come una palla, perde più del suo moto quando urta contro un corpo morbido che contro uno duro, e che essa rotola meno facilmente su un tavolo ricoperto di tessuto che su uno levigato; così l'azione di questa materia sottile può essere frenata molto più dalle parti d'aria che, essendo come sono soffici e debolmente legate una all'altra, non offrono molta resistenza ad essa, che dalle parti dell'acqua, che offrono più resistenza e ancor più dalle parti d'acqua che da quelle del vetro o cristallo...

[*] (Questa materia "molto sottile" è il famoso "etereo luminifero"... ovvero il mezzo entro il quale si sarebbe dovuta propagare la luce, e la cui esistenza è stata definitivamente confutata solo un paio di secoli dopo gli eventi qui narrati).

Fermat racconterà in seguito che

dopo una lunga corrispondenza e molte discussioni ci separammo come l'accusato ed il testimone, l'uno asserendo e l'altro negando i fatti, sebbene alla fine io abbia ricevuto da lui delle lettere molto gentili.

Naturalmente molte di queste missive passavano per le mani di Mersenne, che le divulgava anche ad altre persone: si crearono opposte tifoserie, con battaglie che, se calavano di intensità, Mersenne provvedeva subito a ravvivare!   ▲  

Il "principio del Minor Tempo"

Dopo la morte di Cartesio, Fermat affronta la rifrazione per proprio conto, cercando di spiegarla con argomenti meno discutibili. Ripensa al principio di "minima distanza" di Erone, e lo sostituisce con il principio del "minor tempo", ovvero:

Il percorso fra due punti preso da un raggio di luce è quello che è attraversato nel minor tempo.

Nota: questo principio non invalida le leggi della propagazione e della riflessione: infatti questi fenomeni accadono sempre nello stesso mezzo, quindi a velocità costante; e se la velocità è costante, il percorso più breve (Erone) è anche il più veloce (Fermat).

Il pensiero di Fermat si può spiegare grazie ad una famosa analogia, attribuita a Richard Feynman:



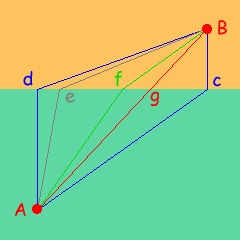
L'Allegro gitante A è andato al mare, e sta annegando. Il Bagnino B lo vede e deve andare a salvarlo. Ammesso che la sua velocità di corsa sulla spiaggia sia maggiore della sua velocità a nuoto nell'acqua, quale percorso deve fare per impiegare il minor tempo?

Se il Bagnino corresse dritto davanti a sé verso il punto c, si troverebbe a dover fare un lungo percorso a nuoto, quindi questa non è la strategia migliore. Il Bagnino allora potrebbe procedere in linea retta, raggiungendo la riva nel punto g; ma viene il sospetto che il percorso in acqua sia ancora troppo lungo, rallentando le operazioni di salvataggio. Allora potrebbe correre fino al punto d, in modo da rendere minima la durata del percorso in acqua; ma vediamo adesso il punto e: la lunghezza del tratto e-a in acqua è quasi identica al precedente tratto d-a; ma il percorso da fare a piedi b-e è sensibilmente più corto di b-d. Insomma, la domanda è: qual è il punto f che rende minore il tempo di salvataggio?

Con questi dati di partenza, che ricapitolo di seguito:

— la luce si muove all'interno di ogni materiale a una velocità costante ben determinata, dipendente solo dal materiale stesso (esattamente come Cartesio);

— il percorso scelto dalla luce per andare da un punto a un altro sarà sempre quello che impiega il minor tempo;

e grazie ai nuovi metodi di calcolo differenziale che aveva scoperto, Fermat ricava la seguente formula:

sen α     v1
-------- = ---- = n
sen β     v2

in cui di nuovo α e β sono gli angoli di incidenza e di rifrangenza, v1 e v2 le velocità nell'aria e nell'acqua, n il coefficiente di rifrazione di Snell.

Fermat rimane molto stupito dal vedere che la "forma" del proprio risultato è molto simile a quello di Cartesio: l'unica differenza sta nel rapporto fra le velocità nell'aria e nell'acqua, che per Fermat è invertito rispetto a quanto sosteneva Cartesio. (Nota: è proprio grazie a questa formula che il Bagnino potrebbe determinare il punto sul bagnasciuga che gli consentirebbe di portare soccorso all'Allegro Gitante nel minor tempo possibile...).

Fermat trasmise queste nuove scoperte a Mersenne, che naturalmente le divulgò agli altri studiosi con cui era in contatto. Ricordo che Cartesio era già morto... ma le polemiche ripresero, forse ancora più aspre di prima: e questo perché i "tifosi" di Cartesio non capirono (o più probabilmente non vollero accettare) i nuovi, straordinari metodi di calcolo di Fermat!

Alla fine Fermat dimostra di avere ragione a sostenere che la velocità della luce è minore nell'acqua; ma soprattutto fonda la sua legge su un principio molto "bello" da un punto di vista fisico, e sicuramente più "solido" della congettura di Cartesio. Ma come dicevo, nonostante sia Cartesio che Fermat fossero francesi, e nonostante che sia il ragionamento che il risultato di Fermat fossero quelli corretti, per i francesi la legge di rifrazione si chiama legge di Snell-Cartesio... c'est la vie!   ▲  

Prossimo capitolo: La Diffrazione