Euclide vs. Hilbert: Punti, Linee e Superfici

Sommario:

+ Elementi di Euclide: Riga e Compasso
– Euclide vs. Hilbert: Punti, Linee e Superfici
      Hilbert: i Fondamenti della Geometria
      Non solo Postulati: le Nozioni Comuni
      Assiomi di Congruenza
      Incongruenze?
      Il nocciolo della questione
      Euclide: la coerenza logica degli Elementi
      Euclide: la Nozione Comune 8 del Libro I
+ Euclide: il Quinto Postulato
+ Elementi di Euclide: Costruzioni elementari

Definizioni

Nel capitolo precedente abbiamo visto alcune Definizioni e Postulati, presenti nel Libro I degli Elementi di Euclide, che specificano il modo d’uso degli strumenti con cui viene identificata la Geometria Classica: la Riga e il Compasso (anche se in realtà Euclide non nomina mai questi strumenti meccanici, dato che si limita a parlare di Linee e di Cerchi).

Torniamo ancora su alcune di queste Definizioni:

[d. 1] — Un punto è ciò che è privo di parti.

[d. 4] — La retta è quella linea che giace sui suoi punti in modo uniforme.

[d. 7] — Superficie piana è quella che giace ugualmente rispetto alle sue rette.

Abbiamo già sottolineato al capitolo precedente come queste non siano definizioni facilmente comprensibili. Certo, sono state scritte più di duemila anni fa: proviamo allora a vedere come se la cavano i matematici moderni.

Ebbene, anche la Geometria moderna parte da alcune definizioni, o Concetti Primitivi; ma di questi, non viene data nessuna definizione. Infatti se definire significa costruire un nuovo concetto a partire da concetti precedenti già definiti, il continuo tornare all’indietro verso concetti che siano precursori di ciò che vogliamo definire dovrà prima o poi arrestarsi da qualche parte, ovvero su qualcosa che non potrà più essere a sua volta definito.

I matematici moderni quindi non definiscono gli enti geometrici primitivi su cui vanno a lavorare, ma definiscono il loro funzionamento attraverso alcuni postulati, o assiomi, che li collegano fra loro. A proposito, prima di andare avanti, sarà forse meglio richiamare il significato delle seguenti parole:

Definizione — spiegazione delle qualità essenziali di qualcosa.

Postulato — enunciato che, pur non essendo dimostrabile, è considerato vero.

Nozione Comune — verità considerata evidente per se stessa, ovvero che non ha bisogno di dimostrazione.

Assioma — termine usato per definire sia i Postulati che le Nozioni Comuni. Come vedremo, la distinzione di Euclide fra Postulati e Nozioni Comuni è stata abbandonata dai matematici moderni, che parlano semplicemente di Assiomi.

Proposizione o Teorema — Risultato matematico dimostrabile sulla base di altre proposizioni precedentemente già dimostrate o assunte come vere.

Nota: In matematica, quando si ha la trattazione di un argomento che si basa su un insieme di Assiomi, al quale fanno seguito tutti i teoremi che ne derivano, si parla di Teoria Assiomatica.   ▲  

Hilbert: i Fondamenti della Geometria



David Hilbert (1862 - 1943), nei suoi fondamentali "Fondamenti di Geometria" del 1899 (scusate il bisticcio!), inizia infatti così:

Consideriamo tre generi di oggetti. Gli oggetti del primo genere saranno chiamati Punti, [...] quelli del secondo Linee Rette, [...] quelli del terzo Superfici Piane [...]

Dobbiamo pensare a questi Punti, Linee Rette e Superfici Piane come a oggetti che hanno certe relazioni reciproche, che indichiamo con parole come "Situato", "Compreso", "Fra", "Parallelo" [...] La completa ed esatta descrizione di queste relazioni derivano dagli Assiomi della Geometria [...] che hanno il compito di definire esattamente ciò che altrimenti sarebbero solo delle cognizioni intuitive.   ▲  

Non solo Postulati: le Nozioni Comuni

Negli Elementi di Euclide, oltre all’elenco dei Postulati, compare una serie di Nozioni Comuni, come per esempio:

[n.c. 1] — Cose che sono uguali ad una stessa cosa sono uguali anche fra loro

[n.c. 8] — Il tutto è maggiore della parte.

A un’occhiata distratta potrebbero essere prese come cose un po’ scontate, ma non lo sono affatto: vedremo ad esempio che la Nozione Comune 1 compare anche fra gli Assiomi di Hilbert (per quanto riguarda invece la numero 8, vedere qualche considerazione in fondo a questa pagina).

In effetti la critica moderna tende a considerare i Postulati e le Nozioni Comuni di Euclide come fossero un unico elenco (di Assiomi, come accennato all'inizio), senza soffermarsi troppo sulle ragioni per cui sono state suddivise in due elenchi diversi. Piuttosto, i problemi su cui i matematici si soffermano (da sempre), e che sono molto più importanti, sono le seguenti:

— Sono tali Assiomi sempre coerenti, o capita che si contraddicono fra loro?

— Sono completi, ovvero non è che magari ne manca qualcuno?

— Sono indipendenti fra loro, ovvero non sarà che qualcuno di essi possa essere ricavato a partire dagli altri?

Nei suoi "Fondamenti di Geometria" Hilbert elenca ventuno Assiomi (quindi in numero maggiore rispetto ai cinque Postulati e alle otto Nozioni Comuni di Euclide). Sono divisi in vari gruppi: Assiomi di Collegamento (relazioni dei punti rispetto alle linee, dei punti e delle linee rispetto ai piani, ecc.); di Ordinamento (relazioni fra i punti di una stessa retta o di uno stesso piano); di Congruenza (criteri di uguaglianza fra segmenti, angoli, ecc.); di Continuità (che per ora non prenderemo in considerazione), e infine l’Assioma delle parallele che, pur se espresso in modo diverso dal famoso Postulato Euclideo delle parallele, definisce lo stesso concetto.

Gli Assiomi di Hilbert sono stati dimostrati essere coerenti, completi e indipendenti: ormai non ci si devono più aspettare sorprese di rilievo nel pensiero geometrico. Interessante è piuttosto confrontare gli Assiomi di Hilbert con quelli di Euclide (ricordo che ci sono più di duemila anni di differenza).

Per esempio, il primo Assioma di Hilbert e il primo Postulato di Euclide sembrano coincidere:

[Euclide, Postulato 1] — Tra due punti qualsiasi è possibile tracciare una ed una sola linea retta.

[Hilbert, Assioma I, 1] — Due punti distinti definiscono completamente una linea retta.

In realtà non sono uguali: per Euclide i due punti sono gli estremi di un segmento, mentre per Hilbert ciò che viene definito è una retta illimitata (o infinita). Infatti le cose proseguono così:

[Euclide, Postulato 2] — Si può prolungare un segmento oltre i due punti indefinitamente.

[Hilbert, Assioma I, 2] — Ogni coppia di punti di una retta individua tale retta.

Già da queste poche righe si intuisce che si tratti di questioni molto sottili, quasi filosofiche. Non voglio ora scrivere qui tutto ciò che ci sarebbe da dire in proposito; mi sembra però molto utile soffermarsi su un gruppo specifico di Assiomi:   ▲  

Assiomi di Congruenza

Ovvero: sui criteri di uguaglianza. Iniziamo da Euclide, che dice:

[n.c. 7] — Cose che coincidono fra loro sono fra loro uguali

Hilbert lo sostituisce con due Assiomi:

[IV, 1] — Ogni segmento è congruente a se stesso

[IV, 4] — Ogni angolo è congruente a se stesso

Sembra che Hilbert si complichi la vita, impiegando due Assiomi per dire la stessa cosa che dice Euclide in uno solo, ma non è così. Infatti Euclide si riferisce genericamente a "cose" che potrebbero essere, oltre che segmenti e angoli, anche poligoni, poliedri, o qualsiasi altro oggetto geometrico. Lo scopo di Hilbert invece è quello di ridurre gli Assiomi al minimo possibile, ovvero di garantirne l'indipendenza; infatti se un Assioma, o una parte di esso, risultasse essere dimostrabile a partire dagli altri, andrebbe annoverato fra i Teoremi. Hilbert giudica invece sufficiente postulare l'auto-congruenza di segmenti e angoli, essendo effettivamente dimostrabile l'auto-congruenza di tutti gli altri oggetti geometrici. Conclusione: i due Assiomi di Hilbert postulano qualcosa di più ristretto rispetto alla singola Nozione Comune di Euclide.

Analogamente avviene per la proprietà transitiva dell’eguaglianza: alla Nozione Comune di Euclide:

[n.c. 2] — Cose che sono uguali ad una stessa cosa sono uguali anche fra loro.

Hilbert lo sostituisce con:

[IV, 2] — Se due segmenti sono congruenti a un terzo segmento, sono congruenti anche fra loro.

[IV, 5] — Se due angoli sono congruenti a un terzo angolo, sono congruenti anche fra loro.

Andiamo oltre. Nella Nozione Comune:

[n.c. 2] — Se cose uguali sono addizionate a cose uguali, le totalità sono uguali.

bisogna intendere bene a cosa si riferisce Euclide. Infatti, finché si tratti di segmenti o angoli, l’enunciato potrebbe andar bene; ma se si parla di superfici potremmo avere questi risultati:



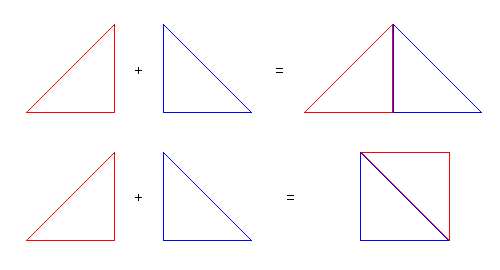
come si vede dal disegno, unendo coppie di poligoni uguali non si ottengono sempre poligoni uguali! Infatti, dall’uso che fa Euclide di questa sua Nozione Comune si capisce che alla parola uguali non dà il significato di congruenza (ovvero di uguaglianza in tutti gli aspetti) ma di equivalenza, nel senso di uguale area complessiva.

In questo senso Hilbert è ancora più stringato che nei casi precedenti, limitandosi ai soli segmenti:

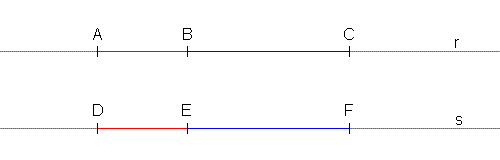
[IV, 3] — Siano AB e BC segmenti su una retta r privi di punti in comune a parte il punto B, e siano DE e EF segmenti su una retta s privi anch’essi di punti in comuniea parte il punto E. Se AB è congruente a DE, e BC è congruente a EF, allora anche AC sarà congruente a DF.   ▲  



Incongruenze?

Per completare il gruppo degli Assiomi di Congruenza di Hilbert, a quelli elencati nel paragrafo precedente bisogna aggiungerne uno:

[IV, 6] — Se per due triangoli ABC e DEF si ha che AB è congruente a DE, AC è congruente ad DF, come pure sono congruenti gli angoli BAC e EDF, allora tutto il triangolo ABC sarà congruente al triangolo DEF.

Detto in altre parole, si tratta del Primo Criterio di Congruenza dei triangoli (che dovremmo ricordare tutti, avendolo imparato alle scuole medie): quello per cui due triangoli sono congruenti se hanno congruenti due loro lati e l'angolo compreso. Lo stesso enunciato, anche se con parole diverse, compare anche negli Elementi di Euclide come Proposizione 4 del libro I:

Se due triangoli hanno due lati rispettivamente uguali a due lati, ed hanno uguali gli angoli compresi fra i lati uguali, avranno anche la base uguale alla base, il triangolo sarà uguale al triangolo, e gli angoli rimanenti del primo saranno uguali ai rispettivi angoli rimanenti del secondo.

Per questa dimostrazione (e per pochissime altre in tutti i suoi Elementi) Euclide ricorre a un sistema di "trasporto meccanico": vediamo come.

Siano dati i due triangoli ABC e DEF, in cui le coppie di lati AB e DE, e AC e DF, sono fra loro uguali (congruenti), così come uguali sono gli angoli in A e in D.



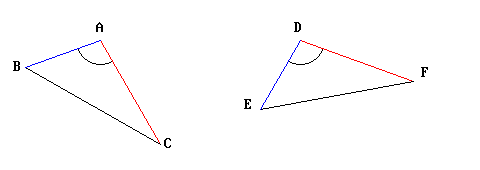
Per prima cosa Euclide sposta il triangolo ABC in modo che il vertice A cada esattamente su vertice D:



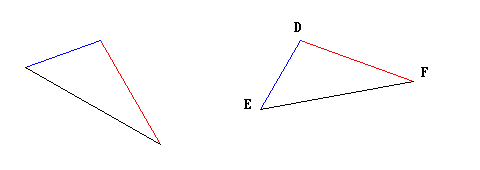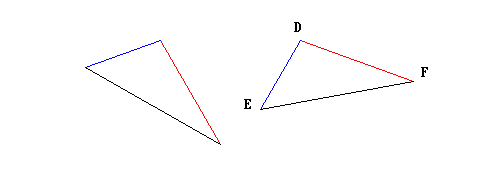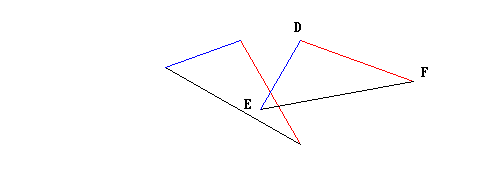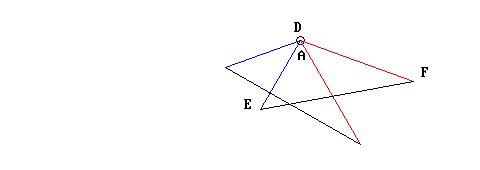
Poi, dopo aver prolungando i lati DE e DF, ruota il triangolo ABC finché il lato AC sia perfettamente allineato con DF; essendo i segmenti AC DF di uguale lunghezza, ovviamente i punti C e F vengono a coincidere (in effetti non sarebbe stato necessario allungare il segmento DF; ma dato che non si poteva dare per scontato che i punti C ed F sarebbero coincisi prima di averlo verificato, tale allungamento serviva per poter comunque procedere all’allineamento richiesto).



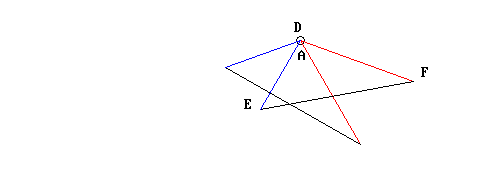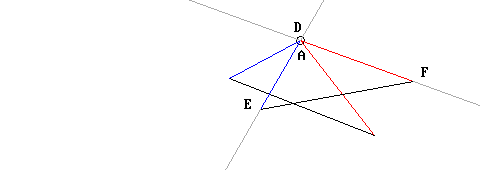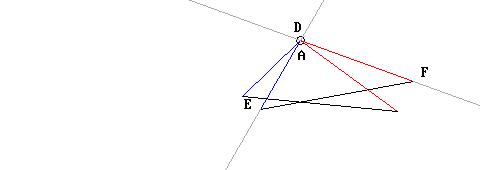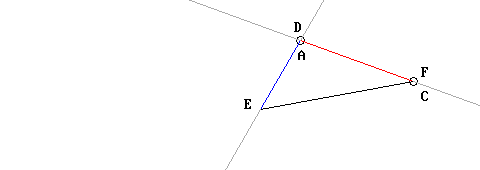
Infine, dato che gli angoli in A e in D sono uguali, anche il segmento AB sarà allineato al DE; ed essendo le lunghezze dei segmenti AB e DE uguali fra loro, anche i punti B ed E vengono a coincidere:



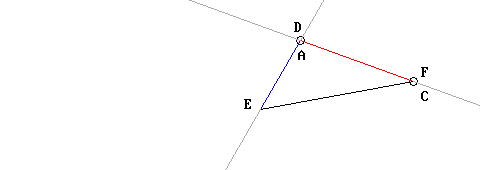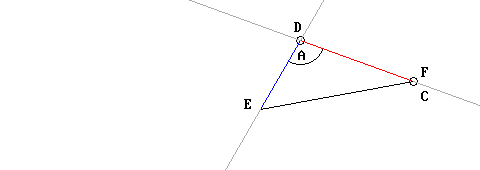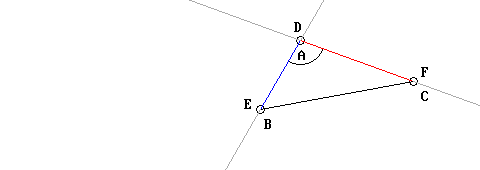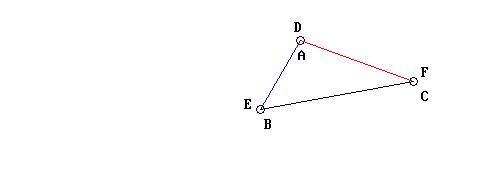
I due triangoli quindi coincidono. E qui entra in ballo la Nozione Comune numero 7 di Euclide, secondo cui cose che coincidono fra loro sono fra loro uguali: si tratta di una sottigliezza notevolissima, degna dei logici matematici moderni! Ricordo infatti che che anche Hilbert enuncia l’auto-congruenza, anche se solo di segmenti e angoli, negli Assiomi IV, 1 e IV, 2.

Il problema che forse non è stato notato finora è che questo criterio di congruenza fra triangoli per Hilbert è un Assioma, mentre per Euclide è una Proposizione, ovvero un teorema compiutamente dimostrato. Come sta la faccenda?   ▲  

Il nocciolo della questione

Ricapitoliamo il procedimento di Euclide, il quale prende due triangoli con due coppie di lati congruenti, come congruente è l’angolo compreso;



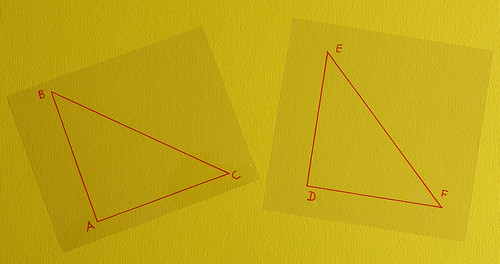
li sovrappone, e vede che tutto coincide:



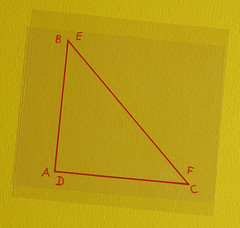
Disponiamo ora i triangoli in questo modo:



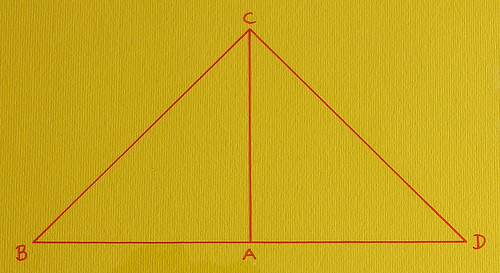
Essendo congruenti gli angoli in A e i segmenti AB e AD, ed essendo il segmento AC in comune, allora tali triangoli dovrebbero essere congruenti. Proviamo però ad applicarli a una superficie non piana, ma cilindrica (vedi qui sotto a sinistra):



Nel disegno di destra i vertici dei triangoli sono congiunti "in linea d’aria", e le linee punteggiate indicano le distanze fra i vertici. Anche se non sembra (per problemi di prospettiva nella foto), le distanze fra i punti AB e AD sono uguali (dato che i relativi segmenti tagliano la superficie del cilindro con la stessa angolazione), mentre i vertici in A sono congruenti e il segmento AC è in comune: allora i due triangoli dovrebbero essere congruenti. Invece non lo sono: infatti la distanza fra B e C è molto più breve di quella fra C e D, essendo il segmento CD parallelo all’asse del cilindro, quindi perfettamente rettilineo, mentre il segmento BC è ortogonale all’asse del cilindro, quindi descrive un arco di cerchio (la cui corda, ovvero la linea punteggiata che unisce in linea d’aria i suoi estremi) non può che essere più breve dell’arco stesso.

Ma se le cose stanno così... vuol dire che né la dimostrazione di Euclide, né l'Assioma di Hilbert sono corretti! Bisogna ricordare però che Hilbert, con i suoi Assiomi non ha mai dichiarato di volersi occupare di triangoli, ma solo di quegli oggetti che ha denominato Punti, Linee Rette e Superfici Piane. Il fatto è che questo Primo Criterio di Congruenza dei triangoli è valido solo in caso di superfici piane; e con questo Assioma Hilbert non si sta occupando specificatamente di triangoli: ci sta piuttosto spiegando come funzionano le sue Superfici piane, ovvero ciò che ha denominato Oggetti del Terzo Genere, all’inizio dei suoi Fondamenti di Geometria.   ▲  

Euclide: la coerenza logica degli Elementi

Nel corso dei secoli gli Elementi di Euclide sono stati analizzati in lungo e in largo, trovandovi più di un punto critico. Per esempio, già nella costruzione di un triangolo equilatero su un segmento dato (Proposizione 1, illustrata nel capitolo precedente) Euclide utilizza il punto di intersezione fra i due cerchi costruiti con centro sulle estremità del segmento e raggio pari al segmento stesso; ma non postula (o dimostra) precedentemente che tali cerchi si incontreranno.

Problemi di coerenza sono stati trovati anche a proposito della Congruenza fra triangoli di cui abbiamo parlato sopra, proprio perché non accenna a requisiti di "indeformabilità". Per questi motivi, le prime quattro Proposizioni del libro I degli Elementi sono oggi considerati alla stregua di Postulati, per cui ne vengono ignorate le argomentazioni dimostrative. E infatti anche Hilbert relega questi enunciati fra i suoi Assiomi.

Questi problemi di logica però non inficiano minimamente la validità degli Elementi di Euclide: tutto ciò che viene dimostrato al loro interno è assolutamente rigoroso e valido; l'unico problema risiede nell'esposizione delle Definizioni, Postulati e Nozioni Comuni, che non reggono all'analisi della logica matematica moderna. Ma se al posto di questi concetti di base di Euclide usiamo gli Assiomi di Hilbert, tutto diventa assolutamente corretto e coerente, confermando la validità di un testo fondamentale e bellissimo nella storia del pensiero umano: non per niente è il testo che vanta il più alto numero di edizioni nella storia, secondo solo alla Bibbia!   ▲  

Euclide: la Nozione Comune 8 del Libro I

"Il tutto è maggiore della parte": sembra un concetto evidente, ma lo è fintanto che si parli di insiemi finiti. Cinque è maggiore di due, un angolo retto è maggiore dell'angolo interno di un triangolo equilatero.

L'affermazione cessa di essere vera quando si abbia a che fare con insiemi infiniti: per esempio, rimanendo nell'ambito della geometria, è assurdo pensare che un segmento corto "contenga" meno punti di un segmento più lungo. E in aritmetica: è assurdo pensare che i numeri pari siano meno di tutti i numeri naturali.

Per chi fosse interessato agli insiemi infiniti, e ai numeri transfiniti, basta che clicci qui.   ▲