+ Elementi di Euclide: Riga e Compasso
+ Euclide vs. Hilbert: Punti, Linee e Superfici
– Euclide: il Quinto Postulato
Cenni storici
Tre ipotesi
Tempi moderni
Dunque?
+ Elementi di Euclide: Costruzioni elementari
In questo capitolo mi occupo delle idee che si sono succedute nei secoli a proposito del Quinto Postulato di Euclide, a partire dai (vani) tentativi per dimostrarlo, all'investigazione di ciò che sarebbe accaduto provando a negarlo, fino alla creazione di quelle che vengono chiamate Geometrie non Euclidee (delle quali fornirò qualche accenno). Ma prima di cominciare, è bene ripetere il testo di Euclide:
Se una retta (c nel disegno sotto) taglia altre due rette (a e b) determinando dallo stesso lato angoli interni (indicati in rosso) la cui somma è minore di quella di due angoli retti, prolungando le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due retti.

Cenni storici
Fra tutte le Definizioni, i Postulati e le Nozioni Comuni di Euclide, questo Quinto Postulato è di gran lunga il più complesso: il suo enunciato infatti sembrerebbe più adatto a un Teorema (o Proposizione) che di un Assioma; ma se fosse un Teorema, dovrebbe poter essere "dimostrato": e su questo i matematici di tutti i tempi si sono accaniti con tutte le loro forze. Euclide stesso avrebbe preferito poterlo ricavare dagli altri postulati; ma non riuscendoci, e avendo bisogno di questa "verità" per dimostrare alcuni dei teoremi che costituiscono i suoi Elementi, decise (provvisoriamente?) di dargli il crisma di "postulato", cioè di verità assoluta.
Nel corso dei secoli i matematici (greci, arabi, rinascimentali) si sono sempre occupati di questo postulato, in qualche caso sostituendolo con altri (anche se si dimostra che queste nuove formulazioni sono sempre equivalenti a quella di Euclide, cioè consentono tutte di giungere alle stesse conclusioni). Ecco la prima, che ci ricorda la faccenda delle rette parallele tagliate da una trasversale che abbiamo studiato a scuola:
Date due rette parallele tagliate da una trasversale, la somma dei due angoli coniugati interni (indicati in rosso nel disegno sotto) è pari ad un angolo piatto.

Ma questo enunciato coincide con la Proposizione 29 del libro I degli Elementi di Euclide: in effetti, Euclide dimostra la Proposizione 29 a partire dal suo Quinto Postulato, mentre altri matematici preferiscono dimostrare il Quinto Postulato partendo dalla Proposizione 29, semplicemente scambiando i ruoli fra il Postulato e il Teorema.
A proposito: abbiamo appena visto comparire il termine "parallela". Per i discorsi che seguono, ci atterremo alla seguente definizione:
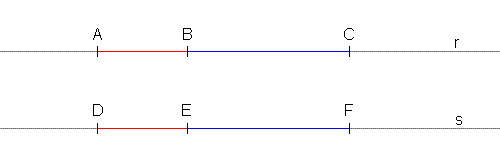
Parallele: due rette nel piano che non si intersecano in nessun punto.La formulazione forse definitiva del quinto postulato di Euclide è dovuta allo stesso David Hilbert che ha scritto i suoi Fondamenti di Geometria. Eccola:
Data una qualsiasi retta a ed un punto P non appartenente ad essa, è possibile tracciare per P una ed una sola retta parallela (in rosso nel disegno sotto) alla retta a data.In realtà si tratta di due affermazioni insieme: quando dice che di rette è possibile tracciarne "una", postula che questa retta esiste; quando dice "e una sola", postula che non possono essere più di una. Di queste due affermazioni, quella che ha valore di Assioma (o Postulato) è solo la seconda: la prima (di esistenza) si riesce a ricavare dagli altri suoi Assiomi. Hilbert stesso spiega la cosa nel seguente modo:
Dal punto P si tracci una linea trasversale che intersechi la retta r in qualsiasi punto A. Si costruisca un angolo in P uguale a quello formato fra la retta r e la trasversale: la retta che si ottiene sarà senz'altro parallela alla retta r data.
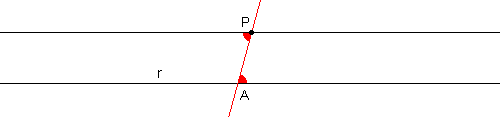
Se così non fosse, allora la nuova retta dovrebbe intersecare la retta r in un qualche punto: diciamo nel punto B. Si trovi allora il punto C tale che la distanza PB sia uguale ad AC, e si congiungano i punti P e B.
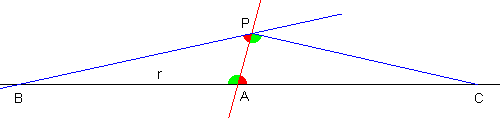
I due triangoli PAB e PAC sono congruenti, in quanto hanno il lato PA in comune, i lati BP e AC anch'essi congruenti, come pure sono congruenti (per costruzione) gli angoli compresi fra dette coppie di lati (PAC e APB, indicati in azzurro).
Ora gli angoli in A (indicati in verde e in azzurro) sono supplementari; e per via della congruenza fra i triangoli, gli angoli corrispondenti in P saranno anch'essi supplementari. Ma quando due angoli sono supplementari e consecutivi, determinano un angolo piatto: quindi i due segmenti BP e PC dovrebbero essere allineati, e dovrebbero fare quindi parte di un'unica linea retta. Ma è impossibile che due rette distinte si intersechino in due punti diversi, B e C!
Questa costruzione potrebbe sembrare del tutto superflua, dato che basta un'occhiata per rendersi conto che c'è qualcosa che non va. Bisogna considerare però che il punto B di "intersezione fra le parallele" potrebbe trovarsi anche a una distanza enorme dal punto A; e a questo punto una semplice occhiata non sarebbe più sufficiente. ▲
Tre ipotesi
Il problema del quinto postulato di Euclide può essere affrontato in un altro modo, mettendolo sotto forma di domanda:
Data una retta r ed un punto P fuori di essa, quante rette si possono tracciare che siano parallele a r e passanti per P?Le ipotesi possibili sono tre:
[a] — una ed una sola (come nel caso descritto sopra).
[b] — nessuna.
[c] — infinite (vedi disegno sotto):
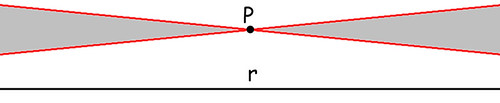
Se fosse vero che le due linee segnate di rosso sono entrambe parallele alla retta r (nel senso di non incontrarla), allora sarebbe parallela anche qualsiasi altra retta passante per P che cada all'interno della zona grigia. Nota: di fatto nel disegno sopra le linee rosse non incontrano quella nera, perché l'area visualizzata è limitata a destra e a sinistra (cioè non è infinita): la difficoltà nell'affrontare il tema delle parallele risiede proprio nel fatto che qualsiasi ragionamento in proposito deve comprendere il concetto di infinito.
L'ipotesi [a], una e una sola parallela, è ovviamente equivalente all'Assioma delle Parallele di Euclide / Hilbert. Ma le altre due? Molti hanno cercato di dimostrarne la condraddittorietà (se ci fossero riusciti avrebbero ottenuto una dimostrazione cosiddetta "per assurdo"). Ma neanche questa via ha portato ai risultati sperati.
Un personaggio notevole è Giovanni Girolamo Saccheri (1667-1733), un gesuita che insegnò filosofia, teologia e soprattutto matematica in vari collegi del suo ordine. Egli volle dimostrare per assurdo il famoso postulato, partendo dal quadrilatero che porta il suo nome:

Il quadrilatero di Saccheri ha due lati opposti a e b di uguale lunghezza, entrambi perpendicolari al lato c. Saccheri prende in esame tre ipotesi sugli altri due angoli (indicati in verde), ossia quelli opposti ai due costruiti retti:
[a] — Gli angoli sono entrambi retti (ciò equivale ad accettare il V postulato)
[b] — Gli angoli interni sono entrambi ottusi (in questo modo si nega il V postulato)
[c] — Gli angoli interni sono entrambi acuti (anche in questo modo si nega il V postulato).
Saccheri riesce a dimostrare correttamente che l'ipotesi degli angoli ottusi è falsa (più o meno con lo stesso procedimento con cui Hilbert dimostra che almeno una parallela deve esistere); per quanto riguarda invece l'ipotesi degli angoli acuti, non riuscì nell'intento: ottenne una dimostrazione che lui stesso riteneva debole, e infatti successivamente ne è stata dimostrata l'inconsistenza. Ma i suoi studi sulle conseguenze della negazione del quinto postulato lo portarono a dimostrare, contro le sue intenzioni, una serie di teoremi che appartengono a sviluppi molto più moderni, riguardanti proprio le Geometrie non Euclidee (di cui mi occupo nei prossimi capitoli). ▲
Tempi moderni
A cavallo fra '700 e '800 diventava più "di moda" che mai cercare la dimostrazione del quinto postulato. Carl Friedrich Gauss (1777-1855, nel ritratto), uno dei più importanti matematici di tutti i tempi, se ne era occupato a partire dai quindici anni di età (!). Nel corso degli anni era passato dalla convinzione della sua validità alla comprensione che geometrie basate sulla sua negazione potevano essere coerenti; però tenne queste considerazioni per sé stesso, senza comunicarle a nessuno. Anche perché...
... il mondo scientifico dell'epoca era sotto il potente influsso di Immanuel Kant (1724-1804) e della sua "Critica della ragion pura". In questo trattato, Kant parla della geometria come di qualcosa che esiste "a priori", cioè ha leggi proprie che non dipendono dall'esperienza, quindi immutabili e assolute. Anni prima Isaac Newton (1643-1727), nei suoi "Principa Mathematica", aveva invece scritto che la geometria era "quella parte della meccanica universale che propone e dimostra l'arte di misurare accuratissimamente", quindi scaturirebbe dall'esperienza più che essere una verità esistente a priori. Anche Gauss la pensa come Newton, ma sa benissimo che molti scienziati e soprattutto filosofi del XIX secolo avrebbero preso per pazzo chiunque sostenesse che esistono geometrie diverse da quella euclidea, proprio per via delle tesi di Kant (a quei tempi andava di moda dire che negare i postulati di Euclide era "commettere un crimine contro l'intelligenza"...). Proprio a proposito di questi signori, in relazione ai suoi studi nella geometria non euclidea, Gauss scrive in una lettera del 1829:
... non mi deciderò ancora per molto tempo a elaborare per una pubblicazione le mie molto estese ricerche sull'argomento, e ciò forse non avverrà mai durante la mia vita, perché temo le strida dei beoti, qualora volessi completamente esprimere le mie vedute…Gauss aveva un amico ungherese, Farkas Bolyai (1775-1856), che aveva dedicato gran parte della sua vita a cercare di dimostrare il quinto postulato. Il figlio di Bolyai, János (1802-1860), si interessò anch'egli all'argomento, tant'è che il padre gli scrisse:
Per amor del cielo, ti imploro di desistere dal tentativo. Il problema della parallele è una cosa da temere ed evitare non meno delle passioni dei sensi, poiché anch'esso può rubarti tutto il tuo tempo e privarti della salute, della serenità di spirito e della felicità.Come spesso accade, i figli non danno ascolto alle raccomandazioni dei padri; e infatti János prosegue le sue ricerche giungendo alla conclusione che il postulato non è dimostrabile e che diverse geometrie coerenti possono essere costruite sulla sua negazione. Scrisse al padre: "Dal nulla ho creato un altro, nuovo universo". Tra il 1820 e il 1823 preparò un trattato su un sistema completo di geometria non euclidea, che fu pubblicato nel 1832 come appendice ad un libro di testo di matematica del padre, con il nome "Appendice che espone in maniera assoluta la vera scienza nello spazio".
Gauss, dopo aver letto quest'appendice, scrisse all'amico Farkas dicendo: "Stimo questo giovane geometra Bolyai un genio di prim'ordine"; ma aggiunse che non avrebbe potuto lodare pubblicamente questo lavoro perché questo sarebbe equivalso a... lodare se stesso, dal momento che lui era arrivato alle stesse conclusioni da molti anni! Il povero János ci rimase malissimo, vedendo sfumare la possibilità di vedersi riconosciuto il merito di queste scoperte. Per giunta...
... negli anni 20 del XIX secolo Nikolaj Lobačevskij (1792-1856) stava compiendo studi sugli stessi argomenti. Anche lui, cercando di dimostrare il postulato delle parallele, arriva invece a costruire un'armoniosa struttura geometrica, assolutamente priva di contraddizioni; e la sua architettura risulta essere più organica e completa di quella del Bolyai. La prima pubblicazione di questi risultati da parte di Lobačevskij precedette quella di Bolyai: ecco com'è che proprio Lobačevskij è considerato il "Copernico della geometria", ovvero colui che scardinò definitivamente la "verità assoluta" della geometria euclidea... con buona pace dei kantiani!
Gauss venne a conoscenza anche dei lavori di Lobačevskij, e lo elogiò ripetutamente... ma solo in privato. Per via della sua paura delle strida dei beoti e dell'avversione di essere trascinato in sterili polemiche, omise di sponsorizzare i lavori di questi due matematici; se lo avesse fatto, le teorie di Bolyai e Lobačevskij si sarebbero diffuse molto più velocemente... insomma alla fine il riconoscimento del loro lavoro è sì arrivato, ma postumo! ▲
Dunque?
Dunque il Quinto Postulato di Euclide si è rivelato essere proprio... un Postulato! È un enunciato che definisce il modo in cui gli enti geometrici (punti, linee) interagiscono fra loro: la sua negazione dà luogo a mondi diversi, ma sicuramente coerenti.
Torniamo un momento alla due concezioni antitetiche di Kant e Newton riguardo alla geometria. Secondo Kant la geometria è qualcosa che esiste a priori, ed è governata da leggi immutabili e assolute; per Newton invece la geometria scaturirsce dall'esperienza. Alla fine, chi ha ragione?
Nel 1870, parlando dei principi della geometria, Hermann von Helmholtz (1821-1894) si esprime così:
Immaginiamo che esistano esseri dotati di ragione, bidimensionali, viventi e moventisi sulla superficie di uno dei nostri corpi solidi. Ammettiamo che essi non possano percepire alcunché fuori da questa superficie. Se tali esseri costruissero la loro geometria, attribuirebbero naturalmente al loro spazio due sole dimensioni. Se essi vivessero sulla superficie di una sfera, formulerebbero un sistema di postulati assolutamente diverso da quelli che potrebbero formulare esseri viventi sul piano, o da noi che viviamo in uno spazio a tre dimensioni.Henri Poincaré (1854-1912) fa un esempio, che cerco di esprimere così: ammettiamo che il mondo sia un disco in cui la temperatura è massima al centro e diminuisca fino allo zero (assoluto) verso la periferia; se il materiale di cui è fatto il disco si dilata in maniera proporzionale alla temperatura, avremo dimensioni dilatate al centro, e ridotte a zero al bordo. Se su questo disco si muovessero esseri bidimensionali come ipotizzato da Helmholtz, e se essi variassero di temperatura a seconda dei loro spostamenti sul disco, ingrandendosi e rimpicciolendo di conseguenza, avremmo due modi diversi di vedere questo strano mondo: per noi si tratterebbe di un semplice disco; per i suoi abitanti il mondo sarebbe infinito, perché via via che si spostano verso il bordo diventano più piccoli, e questo bordo per loro si allontana sempre più.

Quest'immagine è stata ottenuta a partire dalla litografia "Limite del Cerchio III" di Maurits Cornelis Escher (1989-1972), che si è ispirato proprio al lavoro di Poincaré:

Come vediamo, ci si allontana sempre di più dalla concezione euclidea e kantiana di uno spazio esistente a priori, per definire vari tipi di spazio secondo "convenzioni" diverse a seconda delle necessità. Questo concetto è stato espresso da Poincaré: Gli assiomi della geometria non sono né giudizi sintetici né fatti sperimentali: sono convenzioni.
Per Poincaré la scelta fra tutte le convenzioni possibili è guidata da fatti sperimentali, ma resta libera ed è limitata solo dalla necessità di evitare contraddizioni. La domanda sulla verità della geometria euclidea per lui non ha senso: sarebbe come chiedersi se il sistema metrico è vero e gli antichi sistemi di misura falsi.... Insomma non è il criterio della verità che ci deve orientare: una geometria non può essere più vera di un'altra, può essere solo più comoda.
Non c'è dubbio che la geometria euclidea sia per noi la più semplice e si accordi bene con la nostra esperienza; ma per spiegare il mondo che ci circonda questa geometria non è sufficiente: gli sviluppi più clamorosi dello studio di geometrie non euclidee convergeranno in una teoria fondamentale come la Relatività generale di Einstein!
La perdita di "intuitività" della geometria in un certo senso va di pare passo con la sua "assiomatizzazione": i fondamenti della Geometria di Hilbert iniziano con una frase di Kant:
Ogni conoscenza umana parte da intuizioni, procede attraverso concetti e culmina in idee.che però Hilbert ribalta completamente. I risultati della geometria del XIX secolo, a partire dalla crisi della geometria non euclidea, impongono infatti di abbandonare il livello empirico-intuitivo tipico della geometria classica: punti, rette e piani sono semplicemente elementi di insiemi dati; a tale proposito Hilbert dirà che, al posto di punti, rette e piani, si potrebbe parlare di bicchieri, calici e boccali di birra... ▲