Numeri Transfiniti: Aleph-zero

Sommario:

+ I numeri Naturali
– Ancora Aleph-zero
      Numeri Razionali
      Numeri Irrazionali
      Numeri Algebrici
      Numeri Negativi
      Irrazionalità di √2
      Irrazionalità delle radici non intere
+ Il contesto storico
+ Oltre Aleph-zero: il Continuo
+ L'ipotesi del Continuo

Ancora Aleph-zero

Nel primo capitolo di questa "scorribanda" fra gli insiemi infiniti abbiamo scoperto che non si trovano, diciamo così, insiemi infiniti "piccoli". Detto in termini più precisi: non esistono insiemi infiniti di cardinalità, o potenza, minore dell’insieme dei numeri naturali; la cui cardinalità si identifica con la sigla Aleph-0. Ora vogliamo vedere se riusciamo a trovare insiemi infiniti più grandi di Aleph-0.

Per trovare un insieme "più grande" di quello dei numeri naturali bisogna (tenetevi forte!) trovare "un insieme che abbia una funzione iniettiva rispetto all'insieme dei numeri naturali, ma nessuna corrispondenza biunivoca con esso"! Detto in altre parole: occorre scovare un insieme infinito che contenga alcuni membri (in teoria ne basta anche uno solo), che non possa essere messo in corrispondenza con un qualche elemento dell'insieme dei numeri naturali. Si può dire altresì che gli elementi dell'insieme più grande non potranno essere "contati": solo verificando questa condizione saremo sicuri di aver trovato un insieme di cardinalità maggiore di Aleph-0.   ▲  

Numeri Razionali

Possiamo fare un primo tentativo prendendo in esame i numeri razionali, che sono quelli che si ottengono dal rapporto tra due numeri naturali (il termine "razionale" deriva dal latino "ratio", proprio nel suo significato di rapporto). Ogni numero razionale è il risultato di una divisione a/b in cui a è il numeratore e b il denominatore; b deve ovviamente essere diverso da zero, mentre se abbiamo b=1 il risultato è un numero intero: i numeri interi (naturali) sono quindi un sottoinsieme dei numeri razionali.

Nell’intervallo compreso fra ogni coppia di numeri interi consecutivi posso inserire quanti numeri razionali voglio; qui sotto vi mostro una rappresentazione grafica di questo concetto:



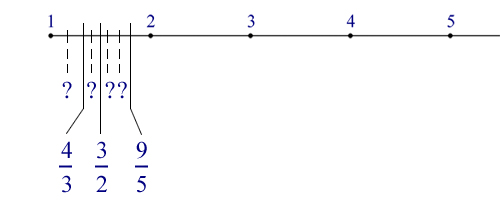
fra i numeri 1 e 2 ho inserito 3/2 (1,5), 4/3 (1,333...), 9/5 (1,8), ovviamente ci sono infinite altre possibilità (ne ho indicate qualcuna con quei punti interrogativi). Calcolando il quoziente fra numeratore e denominatore di ciascuna di queste frazioni si ottiene un numero decimale con un numero finito o addirittura infinito di cifre dopo la virgola (in quest'ultimo caso, come abbiamo imparato alle medie, i decimali saranno periodici).

Ecco, mi vengono in mente almeno tre motivi per cui i numeri razionali dovrebbero essere in quantità maggiore rispetto ai numeri naturali: il fatto che fra ogni coppia di numeri naturali consecutivi posso inserire infinite frazioni; la presenza di tutti quegli infiniti decimali; infine il fatto che ogni numero razionale viene definito da due numeri naturali (numeratore e denominatore). E invece...

#1


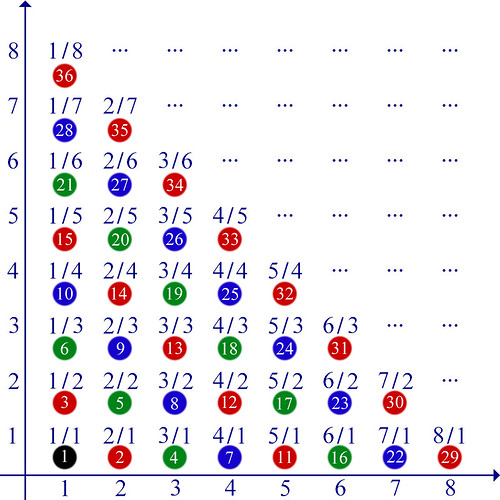
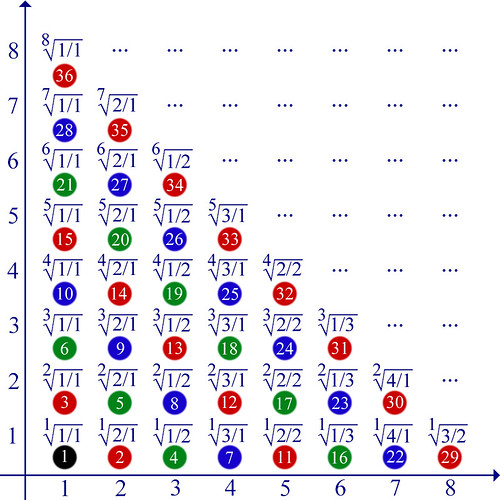
Ecco, in questa griglia ho inserito tutte le frazioni possibili e immaginabili: basta cercare il numeratore sull’asse delle X (orizzontale) e il denominatore sull’asse delle Y (verticale); ovviamente lo schema può essere ingrandito a piacimento. Ho inserito anche dei pallini colorati e numerati: il numero 1 accanto alla frazione 1/1, poi 2 per 2/1 e 3 per 1/2, poi ancora 4 per 3/1, 5 per 2/2 e 6 per 1/3, e così via. In questo modo sto "contando" per diagonali successive tutte le frazioni possibili, anche quelle non ridotte ai minimi termini.

Eccoci quindi al punto: siccome i numeri naturali sono in grado di "contare" le frazioni, e quindi i numeri razionali (*), vuol dire che i due insiemi (dei numeri naturali e dei numeri razionali) possono essere messi in corrispondenza biunivoca, quindi hanno la stessa potenza: sempre Aleph-0.

(*) Precisazione: alcune frazioni che compaiono nella griglia #1 danno luogo allo stesso numero naturale (es. 1/1 e 2/2 = 1) o razionale (es. 1/2 e 2/4 = 0,5); per avere numeri razionali tutti diversi l'uno dall'altro dovrei escludere dal conteggio tutte le frazioni non ridotte ai minimi termini.

Escludere le frazioni non ridotte ai minimi termini è una cosa che si può fare, anche se non è facilissima quando numeratore e denominatore diventano molto grandi. Però si tratterebbe di una fatica inutile:

— l'insieme dei numeri naturali è un sottoinsieme dell'insieme dei numeri razionali (che comprende tutti i numeri naturali)

— l'insieme dei numeri razionali è un sottoinsieme dell'insieme delle frazioni, in quanto più frazioni danno luogo allo stesso numero razionale

— nella griglia #1 ho mostrato la corrispondenza biunivoca fra gli insiemi dei numeri naturali e delle frazioni, che sono quindi equipotenti e di cardinalità Aleph-0.

— allora anche l'insieme dei numeri razionali, che è apparentemente "compreso", come potenza, fra gli altri due, non può che avere potenza Aleph-0 (ometto la dimostrazione rigorosa).   ▲  

Numeri Irrazionali

Facciamo un altro tentativo: proviamo con i numeri irrazionali, come la radice quadrata di due. Questo numero ha una lunga storia: per il teorema di Pitagora la radice quadrata di due coincide con la lunghezza della diagonale di un quadrato di lato unitario:



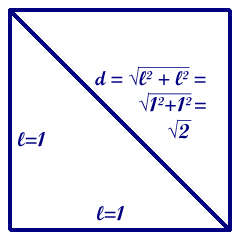
Pitagora era un entusiasta sostenitore della "comprensibilità" dell’universo, nel senso che cercava di "misurarne" i segreti in termini di rapporti. Per esempio aveva studiato le note musicali scoprendo che hanno fra loro delle relazioni "razionali"; aveva anche immaginato il sistema delle "sfere celesti" come supporto per i pianeti e le stelle fisse, sfere sempre in rapporto razionale fra loro; e mescolando le note musicali con le sfere celesti aveva immaginato quella che ancora oggi chiamiamo "armonia delle sfere".

Insomma Pitagora era felicissimo di avere trovato... proprio il teorema di Pitagora! Però ci rimase molto male quando scoprì che la radice quadrata di due non è un numero razionale. Mettetevi nei suoi panni: vuole capire l’universo mondo, scopre un teorema straordinario che lo può aiutare a capirlo meglio, e il primo risultato che trova sfugge al suo criterio su cosa è razionale e cosa non lo è (per la dimostrazione della non razionalità del numero radice di due, vedi sotto). In altre parole: riesce a dimostrare che la radice di due non può essere definita da nessuna frazione a/b, in cui a e b siano numeri interi.

In epoca più moderna è stato dimostrato un teorema molto più generale (vedi ancora sotto), che dice che ogni radice di qualsiasi grado, di qualsiasi numero naturale, può dare come risultato o un numero intero o un numero irrazionale; numeri razionali, mai.

Insomma stiamo scoprendo una quantità enorme di numeri che non sono razionali. Il fatto di non esserlo, vuol dire che la loro rappresentazione decimale non presenterà nessun carattere di periodicità, avendo sequenze infinite di cifre decimali in successione, diciamo così, caotica. Questa cosa trova una facile spiegazione: se ricordate la matematica delle medie, ci avevano insegnato a trovare la "frazione generatrice" dato un qualunque numero decimale periodico, con o senza antiperiodo. Quindi se i numeri irrazionali, come la radice di due, fossero numeri decimali periodici, avrebbero la loro bella frazione generatrice... e allora sarebbero razionali e non più irrazionali.

Questi numeri irrazionali sono degli ottimi candidati per vedere se possono dar luogo a un insieme infinito più grande, ovvero di cardinalità più grande, rispetto all’insieme dei numeri naturali. Ma come ormai vi aspetterete... non è così! Infatti posso usare lo stesso "trucco" usato per i numeri razionali: invece di mettere nel grafico tutte le frazioni possibili, metto tutte le radici possibili. Quindi avrò la riga delle "radici prime" (di fatto, la riga dei numeri naturali); poi la riga delle radici quadrate, delle radici cubiche, poi delle radici quarte, quinte eccetera. E tutte queste radici le potrò numerare per diagonali, come avevo fatto con le frazioni: quindi neanche in questo caso ho ottenuto il mio scopo!

#2


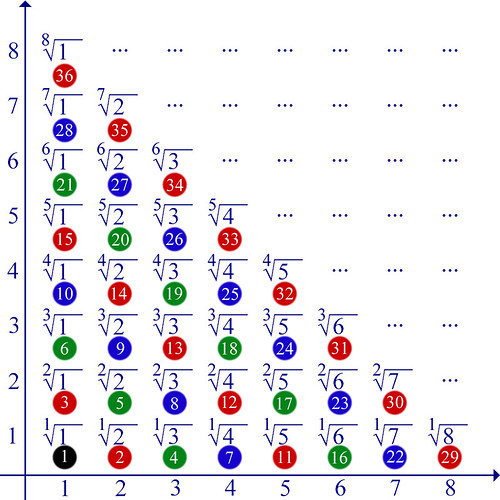
Per le radici di numeri che danno luogo a numeri interi, come radice quadrata di 4 o radice cubica di 27, vale lo stesso discorso fatto qui sopra per i numeri razionali.   ▲  

Numeri Algebrici

C’è un piccolo problema: il nuovo "conteggio" visto sopra lascia fuori i numeri razionali, per esempio la frazione 2/3 non è compresa. Come fare per mettere insieme le due classi di numeri? Beh, basta fare un doppio conteggio. Nella tabella #1 avevamo contato i numeri razionali: se sostituiamo i numeri sotto radice nella tabella #2 con le loro frazioni corrispondenti, otterremo una tabella in cui compaiono tutte le radici (radici di ogni grado) di tutti i numeri i razionali; quindi:

— le radici di primo grado delle frazioni con l’unità al denominatore danno luogo ai numeri naturali;

— le radici di primo grado dei numeri razionali danno luogo ai razionali stessi;

— tutte le radici di secondo, terzo grado e oltre, danno luogo a tutte le radici possibili, dei numeri naturali come dei numeri razionali.

#3


Possiamo immaginare a questo punto di complicare le cose quante volte si vuole: troveremo sempre il modo di "contare" espressioni algebriche sempre più complicate, senza mai trovare un insieme infinito di cardinalità superiore ad Aleph-0!

Nella griglia #3 sto mettendo in corrispondenza i numeri naturali con espressioni del tipo radice ennesima di a/b. Anche qui, molte espressioni possono dar luogo allo stesso numero, intero, razionale o irrazionale che sia; vale comunque lo stesso ragionamento già fatto qui sopra.   ▲  

Numeri Negativi

Ma ora che mi viene in mente, come la mettiamo con lo zero e i numeri negativi? A questo punto è semplice: basta fare una conversione di questo tipo:

1  —    0
2  —    1
3  —  –1
4  —    2
5  —  –2
6  —    3
7  —  –3
...

In sostanza sto mettendo in corrispondenza biunivoca la serie dei numeri naturali (numeri di sinistra) con lo zero e i numeri interi di entrambi i segni (a destra). Naturalmente possiamo sostituire a ogni numero di destra (senza segno) la rispettiva frazione, o radice, o radice di frazione, o qualsiasi altra espressione algebrica che vogliamo!

Da ciò che abbiamo visto in questa e nel capitolo scorso, gli insiemi dei numeri naturali; gli insiemi apparentemente "più piccoli" come i soli numeri pari, o i quadrati, o i numeri fattoriali; e gli insiemi apparentemente "più grandi" come i numeri razionali, irrazionali, e algebrici, anche considerando il segno... tutti questi insiemi sono equipotenti, e hanno cardinalità Aleph-0!   ▲  

Irrazionalità di √2

Questa dimostrazione compare negli "Elementi" di Euclide, ed è basata su un ragionamento per assurdo.

Sia [AB] il lato e [AC] la diagonale di un quadrato, e si supponga che i due segmenti stiano tra loro come la frazione m/n, ridotta ai minimi termini. Allora:

[AC]² : [AB]² = m² : n²

Ma, per il teorema di Pitagora:

[AC]² = 2 ּ [AB]²

E quindi:

m² = 2 ּ n²

Ne consegue che m², e perciò m, è pari. Deve dunque essere dispari il numero n. Poniamo allora

m = 2 ּ q

Allora

m² = 4 ּ q² = 2 ּ n²
2 ּ q² = n²

Di conseguenza n² è pari. È quindi pari anche n, che si è dimostrato dover essere dispari. Ne nasce un’incompatibilità che prova l’asserto.   ▲  

Irrazionalità delle radici non intere

"Siano a ed n due numeri naturali. Se la radice a-ma di n non esiste nel campo nei numeri interi, essa non esiste neppure nel campo dei numeri razionali."

Lo si dimostra per assurdo. Sia x = p / q un numero razionale tale che xª = n, con p e q primi tra loro. Allora anche pª e qª sono primi tra loro.

Dovendo essere n = xª = (p / q)ª, risulta pª = n ּ qª e perciò qª è un divisore di pª. Ma pª e qª sono primi tra loro, e ciò può avvenire soltanto se qª = 1. Sarebbe allora x = p / 1, un numero intero, contrariamente all'ipotesi.   ▲  

Prossimo capitolo: Il contesto storico