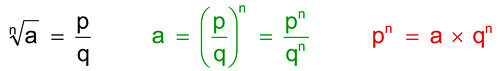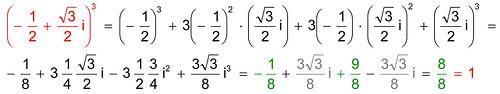Sommario:+ Contare+ Sistemi di numerazione+ Addizione e Sottrazione+ Moltiplicazione+ Divisione– Radice Quadrata Perché la radice quadrata? Il metodo classico di calcolo I "Bastoncini di Nepero" I Numeri Irrazionali I Numeri Immaginari Equazioni di Terzo Grado I Numeri Complessi Il Piano Complesso L'Equazione Ciclotomica L'Equazione Ciclotomica Niccolò Tartaglia+ Elevamento a potenza+ Logaritmi+ Il Regolo CalcolatoreQuando ero ragazzo odiavo le radici quadrate, non tanto in sé, ma perché non capivo il motivo di quel metodo così complicato per calcolarlo. Se anche a voi è rimasta questa curiosità, leggete qui sotto: non era poi una cosa così astrusa!Perché la radice quadrata?La radice quadrata non serve spesso nell'uso quotidiano, mentre in campo scientifico salta fuori da tutte le parti! Vediamo però un (im)probabile caso in cui anche a voi potrebbe capitare di averne bisogno!
Uno zio d'America mi ha lasciato in eredità un terreno di forma perfettamente quadrata e della superficie di 56250 metri quadrati. Lo voglio recintare: quanta rete devo comprare? Lo voglio sapere esattamente: non ne voglio sprecare neanche un centimetro!
Il perimetro di questo quadrato è quattro volte il lato; e siccome l'area di un quadrato è... il quadrato del lato, allora per saperne il lato devo fare l'operazione inversa, cioè devo estrarre la radice quadrata dell'area.
Il calcolo si esegue per approssimazioni successive, come si fa con con la divisione: si ricava la cifra più significativa del risultato e si calcola il resto; poi si ricava una nuova cifra, un nuovo resto, e così via.
▲ Il metodo classico di calcoloIl calcolo va impostato come mostro qui sotto, raggruppando a coppie le cifre del numero di cui si cerca la radice (radicando) partendo da destra: prima le cifre delle unità e decine, poi centinaia e migliaia, e così via. Il gruppo di sinistra alla fine sarà costituito da una o due cifre (in questo caso dalla sola cifra 5, indicata in nero): è proprio da qui che inizierà il calcolo.
(Questo raggruppare le cifre a coppie dipende dal fatto che il quadrato di 10 è 100. A ogni cifra del risultato corrispondono due cifre del radicando; e il risultato della radice avrà tante cifre intere quanti sono i gruppi di due cifre in cui è stato diviso il radicando).
La prima cifra del risultato va determinata cercando il massimo numero (da 1 a 9) il cui quadrato sia minore o uguale al gruppo di sinistra delle cifre del radicando. Nel nostro caso 2 x 2 = 4 che è minore di 5. Sotto al segno di radice si calcola il Resto, ovvero la differenza fra il 5 del radicando e il 4 che abbiamo appena trovato.
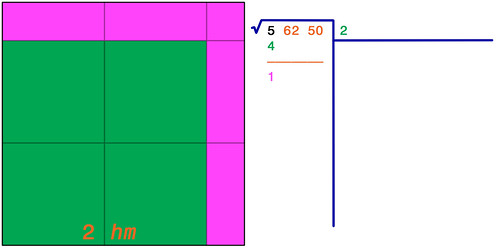
Questa prima cifra del risultato, che sappiamo essere la cifra delle centinaia (di metri), indica proprio il numero intero di ettometri che stanno nel lato del quadrato.
Nel disegno sopra le righe orizzontali e verticali rappresentano divisioni del terreno in quadrati di 100 metri di lato, a partire dall'angolo inferiore sinistro: dal disegno è subito evidente che il numero di ettometri che stanno nel lato è due, e che gli ettari interi che stanno nel quadrato è 4. Dal disegno appare ovvio che nel quadrato non ci potrebbero stare 3 x 3 = 9 ettari: ecco perché, come primo passo nel calcolo della radice quadrata, si cerca proprio il numero più alto il cui quadrato non sia maggiore del primo gruppo di cifre del radicando.Per andare avanti con il calcolo bisogna considerare non più le centinaia ma le decine di metri (decametri). Aggiorno lo schema:
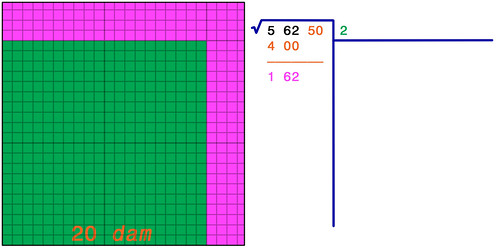
La griglia ora rappresenta decametri; l'area verde ha le stesse dimensioni del disegno precedente, solo che il lato è espresso in decametri invece che in ettometri; ogni quadratino quindi è un'ara (decametro quadrato), e l'area verde (4 ettari) ha adesso una superficie di 400 are.
Per trovare la cifra successiva del risultato bisogna prendere in esame anche il gruppo successivo di due cifre del radicando (62): il numero complessivo 562 nel nostro caso rappresenta la superficie in are intere (senza decimali) del terreno.
Per esprimere anche il Resto in are si calcola la differenza fra 562 are meno 400 are (area corrispondente alla prima cifra già trovata del risultato): il Resto è quindi di 162 are. Adesso bisogna trovare la seconda cifra (c) del risultato.
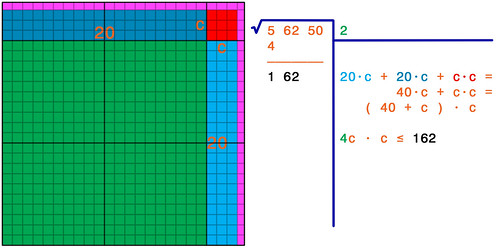
La cifra c determina il valore delle due aree celesti (ciascuna delle quali è un rettangolo con un lato di 20 decametri e l'altro che vale proprio c) e dell'area rossa (che è un quadrato di lato c). Queste tre aree sono indicate, nei rispettivi colori, nell'espressione sulla destra.
Il nostro scopo è trovare il massimo valore di c tale che la somma delle aree dei due rettangoli e del quadrato non superi il valore del Resto (162). Semplifichiamo l'espressione delle aree: nella riga sottostante sostituisco la somma di due volte 20 per c con 40 per c; poi prendo c a fattor comune ricavando l'espressione (40+c) per c; ma siccome c può essere solo una cifra compresa fra 0 e 9, riduco il tutto all'espressione 4c per c, in cui 4c è un numero di due cifre composto dal 4 (decine) e da c (unità): in pratica sostituisco la cifra 0 del 40 con la cifra c.
Il valore "4c per c" è l'area complessiva dei due rettangoli celesti più il quadrato rosso, e quest'area complessiva non deve superare l'area residua (il numero indicato in nero); la seconda cifra (c) del risultato va quindi cercata come il valore massimo che, inserito nell'espressione 4c per c, dia un valore minore o uguale al Resto (162). Il valore cercato è tre:
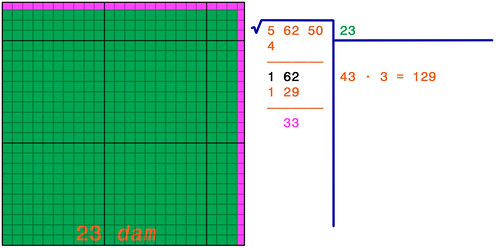
Il risultato, che ora ha due cifre, ci dice che il lato del quadrato verde è 23 decametri, e che una volta tolte dal Resto precedente (162) le aree rettangolari di cui ci siamo occupati sopra (129), il nuovo Resto è di 33 are (indicate in viola).
Ancora una volta, per andare avanti con il calcolo bisogna ridurre la scala, passando dai decametri ai metri, e della are ai metri quadri.
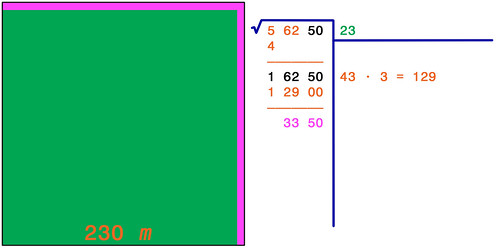
Qui la griglia non c'è più, perché risulterebbe troppo fitta. L'area verde è la stessa del disegno precedente, solo che il lato è espresso in metri invece che in decametri. Sotto al segno di radice va aggiornato il calcolo del Resto in modo da considerare metri quadri: ecco che il Resto precedente, che era di 162 are, una volta calate le ultime due cifre del radicando diventa di 16250 metri quadri; sottraendo i 12900 metri quadri del calcolo precedente (129 are), rimane un Resto di 3350 metri quadri (in viola): in base a questo nuovo Resto si cerca la terza cifra (c) del risultato.
Il calcolo avviene esattamente come nel caso precedente: la cifra delle unità del risultato (metri) è 7.
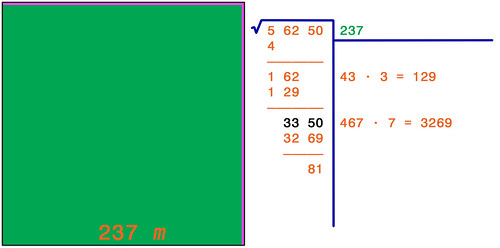
Con questo è finito il calcolo della parte intera del risultato. Ma all'inizio ho detto che volevo il valore esatto
al centimetro: si può procedere come si fa con la divisione, "calando" degli zeri da aggiungere al Resto; solo che, a differenza della divisione, nel calcolo della radice vanno aggiunti zeri a coppie. Vediamo i due passi successivi del calcolo:
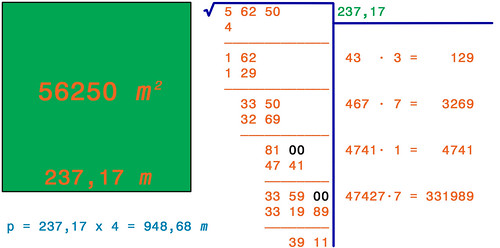
Alla fine, il risultato della radice è di 237 metri e 17 centimetri. Moltiplicando questo risultato per quattro ottengo il perimetro del terreno: 948,68 metri, ed è proprio la quantità di rete che acquisterò per realizzare la mia recinzione!
Qui di seguito ricapitolo le regole per il calcolo della radice, così come ce le hanno insegnate a scuola:
1 — Si raggruppano le cifre del radicando a coppie, da destra a sinistra
2 — Si calcola il numero più grande il cui quadrato non sia superiore al gruppo di cifre di sinistra; questo numero è la prima cifra del risultato, e il suo quadrato va sottratto dal gruppo di due cifre di sinistra del radicando, in modo da ottenere un Resto.
3 — Si calano le due cifre successive dal radicando in modo da completare il Resto; se le cifre del radicando sono esaurite, si aggiungono due zeri.
4 — La cifra c successiva del risultato va calcolata cercando il massimo valore di c tale che, calcolando il prodotto di c per un numero che è il doppio del risultato della radice già calcolato e al quale si affianca a destra la cifra c, si ottiene un risultato che non supera il Resto determinato al punto precedente. Quella trovata è la nuova cifra del risultato.
5 — Si sottrae il prodotto di cui al punto precedente dal Resto determinato al punto [3].
6 — Si riprende dal punto [3] fino ad esaurire le cifre del radicando, casomai con tanti passaggi in più quante sono le cifre decimali desiderate. ▲ I "Bastoncini di Nepero"Ho già spiegato il funzionamento dei "bastoncini di Nepero" per quanto riguarda le
moltiplicazioni e le
divisioni: ora è il turno delle radici quadrate.
Per eseguire questo calcolo occorre un bastoncino in più di larghezza doppia (quello di destra nella foto che segue):
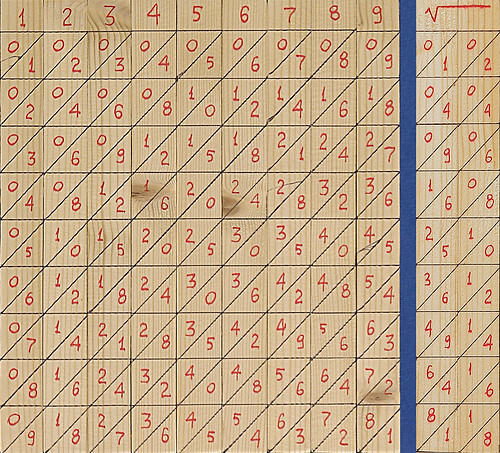
Il bastoncino di destra presenta due colonne: quella di sinistra i quadrati dei numeri da 1 a 9; quella di destra il doppio degli stessi numeri. Vediamo come si esegue, con questo armamentario, il calcolo della stessa radice che abbiamo visto sopra.
La prima cifra del risultato si calcola come descritto nella puntata precedente: usando il solo bastoncino delle radici, si trova qual è il quadrato più grande che sta nel primo gruppo di cifre del radicando (il cinque scritto in rosso).
Questo quadrato è 4 (evidenziato in giallo), corrispondente alla riga 2 (evidenziata in verde). Il 2 quindi è la prima cifra del risultato; il quadrato va sottratto dalla cifra 5 del radicando, ottenendo un Resto pari a 1.
Ora va usata la colonna di destra del bastoncino delle radici: il valore evidenziato in celeste va trascritto sulla destra (vedremo fra un po' a cosa serve):
Alla sinistra del bastoncino delle radici va aggiunto il bastoncino corrispondente al numero evidenziato in celeste (4), poi si completa il Resto calando altre due cifre dal radicando (62, indicate in rosso):
Si cerca sui bastoncini il "Totale" più alto possibile che stia nel Resto. Questo totale è 129 (evidenziato in giallo), che si trova sulla riga 3 (evidenziata in verde): il 3 è la nuova cifra del risultato, che va trascritta accanto al 2 trovato in precedenza. Alla fine il Totale va sottratto dal Resto.
Adesso il numero di destra del bastoncino delle radici (evidenziato in giallo) va aggiunto al 4 evidenziato in celeste secondo il calcolo che si vede sulla destra. Quello che si ottiene è il valore doppio delle cifre già trovate del risultato (23 x 2 = 46):
Questo 46 va composto alla sinistra del bastoncino delle radici, poi si completa il Resto calando altre due cifre dal radicando (3350, indicato in rosso):
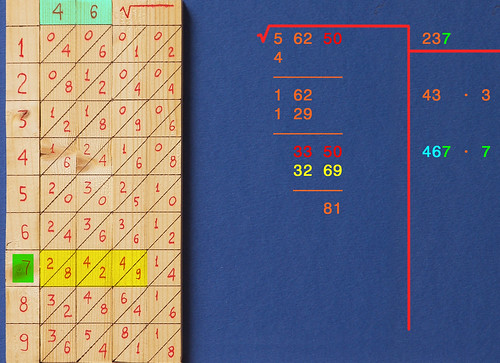
Di nuovo si cerca sui bastoncini il Totale più alto possibile che stia nel Resto. Questo totale è 3269 (evidenziato in giallo), che si trova sulla riga 7 (evidenziata in verde): il 7 è la nuova cifra del risultato, che va trascritta accanto al 23 trovato in precedenza. Alla fine il Totale va sottratto dal Resto.
Il numero di destra del bastoncino delle radici (evidenziato in giallo) va aggiunto al 46 evidenziato in celeste secondo il calcolo che si vede sulla destra. Quello che si ottiene è il valore doppio delle cifre già trovate del risultato (237 x 2 = 474).
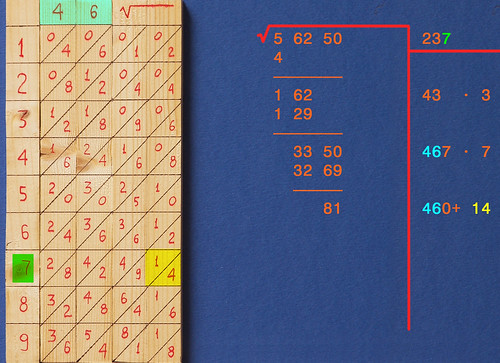
Il 474 va composto alla sinistra del bastoncino delle radici, poi si completa il Resto aggiungendo una coppia di zeri (8100):
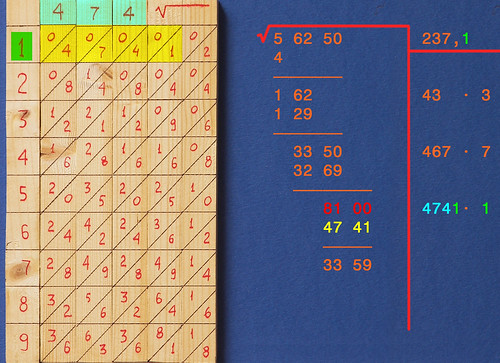
La nuova cifra del risultato è 1. Di nuovo:
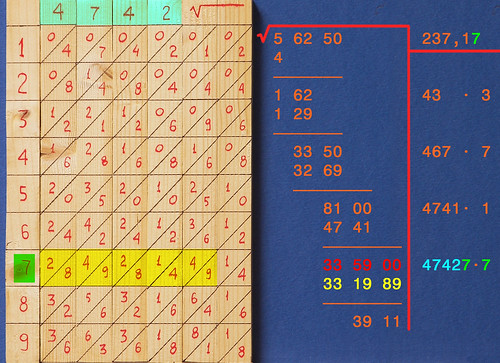
Tutto questo procedimento è un po' macchinoso, comunque consente di verificare al volo qual è ogni cifra da aggiungere al risultato, in quanto i bastoncini consentono di calcolare con facilità tutti i prodotti necessari. Sicuramente un metodo migliore rispetto alle sole carta e penna!
▲ I Numeri IrrazionaliL'aritmetica nasce come arte di fare calcoli sui
numeri naturali. Nei capitoli precedenti abbiamo visto comparire nuove classi di numeri, rese necessarie proprio dai calcoli che si fanno in aritmetica. Infatti:
— Addizione e Moltiplicazione di numeri naturali sono le uniche operazioni che danno sempre come risultato altri
numeri naturali.
— La Sottrazione può dare come risultato un numero naturale, oppure zero oppure numeri negativi: ecco nascere la classe dei
numeri interi (con segno), che comprende ma espande i numeri naturali. Qualunque operazione di somma, sottrazione o moltiplicazione di numeri interi dà come risultato un altro numero intero.
— La Divisione dà luogo ai
numeri razionali, cioè quei numeri che, essendo il risultato di una divisione fra numeri interi, presentano cifre decimali dopo la virgola in numero finito o infinito (in quest'ultimo caso i decimali sono sempre periodici). La classe dei numeri razionali comprende quelle dei numeri interi (e a maggior ragione anche i numeri naturali); qualunque delle quattro operazioni aritmetiche venga fatta su numeri razionali dà come risultato un altro numero razionale.
Stando così le cose, verrebbe da pensare che la classe dei numeri razionali comprenda tutti i numeri possibili e immaginabili... ma non è così: comincia ora un'avventura che apre nuovi, inaspettati orizzonti!
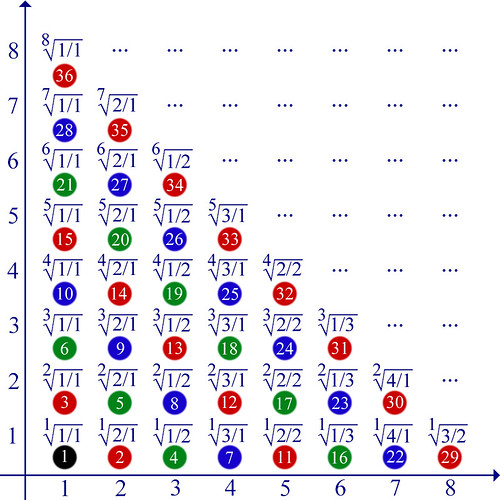
Ripartiamo dalle definizioni: dato un numero qualsiasi, la sua radice quadrata è quel numero che, moltiplicato per se stesso, dà il numero dato (radicando).
Allo stesso modo si definisce la radice cubica:
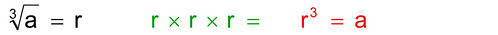
In generale si può definire la radice ennesima di un numero:
Ora viene una domanda. Queste operazioni danno risultati che rientrano sempre nella classe dei numeri razionali? La risposta è no, e la dimostrazione è relativamente semplice:
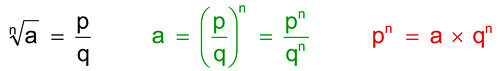
Ammettiamo che la radice ennesima di un numero naturale
a possa essere espresso da una frazione fra numeri naturali (interi)
p e
q, e che questa frazione sia ridotta ai minimi termini (
p e
q non hanno fattori in comune). Elevando alla potenza
n (espressione verde), a sinistra dell'uguale sparisce il segno di radice, mentre a destra abbiamo
p e
q elevati all'ennesima potenza: visto che
p e q non avevano fattori in comune, dopo quest'operazione continuano a non averne. Rigirando l'equazione si ottiene (a destra) che
p alla
n deve essere multiplo di
q alla
n; ma dato che
p e q sono primi fra loro, l'espressione può essere vera solo se
q vale
1, nel qual caso la frazione
p / q è un numero intero. Conclusione: la radice ennesima di un numero qualsiasi può dare come risultato solo un numero intero, oppure un numero irrazionale.
L'esistenza dei
numeri irrazionali è nota dalla più remota antichità: già i pitagorici avevano scoperto che la radice quadrata di due (che da un punto di vista geometrico rappresenta il rapporto fra diagonale e lato di un quadrato) non poteva essere espressa sotto forma di frazione. Quindi le radici ampliano ulteriormente il concetto di numero, aggiungendo ai naturali, interi (con segno) e razionali, anche i
numeri irrazionali.
Nota: i numeri irrazionali non possono essere mai periodici; se lo fossero, si potrebbe ricavarne una frazione generatrice (vedi qui), e allora... non sarebbero più irrazionali! ▲ I Numeri ImmaginariPassiamo ora a vedere una conseguenza davvero "rivoluzionaria" nel calcolo delle radici quadrate. Quanto fa la radice quadrata di -1? Se ricordate qualcosa dell'algebra, meno per meno fa più; quindi sia 1 che -1, elevati al quadrato, danno 1 positivo:
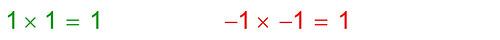
Sembra quindi che in nessun caso si potrà trovare un numero che, elevato al quadrato, dia il risultato -1. Invece la radice cubica di -1 si può fare, infatti meno per meno per meno (tre meni) dà meno:
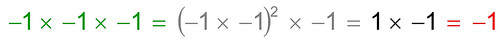
Armeggiando con ragionamenti di questo tipo si vede come l'estrazione delle radici di ordine dispari (terza, quinta, ecc.) di un numero negativo sia sempre possibile, mentre le radice di ordine pari (seconda, quarta, ecc.) non lo è. Ma ne siamo proprio sicuri?
Nel corso dei secoli i matematici hanno dovuto imparare a
non farsi spaventare da concetti scomodi, o anti intuitivi. Così è stato per lo zero e i numeri negativi, per i numeri irrazionali, come anche c'è stata qualche difficoltà ad accettare i numeri razionali con infiniti decimali. Per quanto riguarda la radice quadrata dei numeri negativi, non se ne capiva il senso, e sembrava ovvio che non si sarebbe mai avuto bisogno di loro. Ma la storia della matematica... è piena di sorprese!
▲ Equazioni di Terzo GradoAll'inizio del XVI secolo si discuteva molto del metodo per risolvere le equazioni di terzo grado. Ci furono in proposito grosse dispute e "disfide" fra i matematici dell'epoca (ne parlo
qui sotto), finché una formula generale per la risoluzione di queste equazioni fu trovata. Ma fu trovata anche una grossa pietra d'inciampo con questo caso:
Risolvere questa equazione significa trovare i valori di X per cui l'espressione alla sinistra dell'uguale diventa zero. La formula risolutiva si sapeva essere questa:
in cui compare per due volte proprio la radice quadrata di -1 (evidenziata in rosso). Per l'appunto si sapeva che questa equazione di terzo grado aveva una soluzione valida per X = 4; infatti:
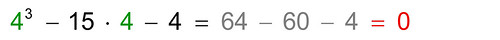In verde indico le sostituzioni di X con 4; in grigio il passaggio intermedio e il risultato in rosso. Allora la domanda era: come può un risultato valido saltar fuori da una formula apparentemente assurda?
Col tempo i matematici, a partire da Raffaele Bombelli (1526-1572) si sono rassegnati ad ammettere l'esistenza di una nuova, strana entità, chiamandola con il significativo nome di "unità immaginaria". In sostanza si definisce:
L'unita immaginaria
i è quel numero che, moltiplicato per se stesso, dà -1. Non è necessario "capirne" il significato, è un "oggetto" matematico sul quale si può lavorare anche senza sapere esattamente cosa sia. Per fare un esempio, se si prende la formula risolutiva dell'equazione di terzo grado che ho mostrato sopra, e si sostituisce la radice quadrata di -1 con la lettera
i, e poi si elabora opportunamente la formula stessa tenendo presente che
i x
i fa -1, si trova che il risultato è effettivamente X = 4.
Insomma le radici hanno aggiunto alla matematica i numeri non solo irrazionali, ma anche immaginari... ma non basta ancora, le radici hanno un'altra peculiarità molto interessante!
▲ I Numeri ComplessiPiù sopra abbiamo cercato la radice quadrata di -1 provando con i valori 1 e -1, ma abbiamo visto che in nessun modo si trovava il risultato cercato (tant'è che si è dovuta ammettere l'esistenza dell'unità immaginaria). Guardando meglio a questi tentativi, si scopre però che le radici quadrate di 1 in realtà sono due, non una; non solo 1 è la radice quadrata di 1, ma lo è anche -1:
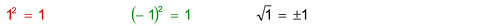
Ora è ovvio che anche la radice quarta di 1 ha queste stesse radici, infatti
Ma la radice quarta di 1 ne ha anche altre due: infatti anche i e -i sono radici quarte di 1.
E la radice cubica? Voglio dire, se la radice quadrata ha due radici e la radice quarta ne ha addirittura quattro, possibile che la radice cubica abbia una radice sola? Ebbene, la radice cubica di 1, oltre all'unità, ha anche due radici strane:
(per chi ne abbia voglia, scrivo la dimostrazione che il cubo della prima di queste espressioni, quella rossa, dà veramente 1):
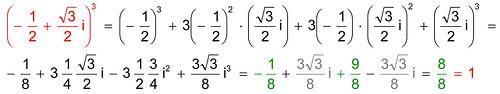L'espressione viene sviluppata secondo il cubo del binomio, e tenendo sempre presente che i x i fa -1; nella riga in basso, i termini grigi si elidono, quelli verdi concorrono a formare l'unità del risultato.Vediamo meglio la struttura di queste radici cubiche di 1: sono costituite da una parte reale (-½) e una immaginaria (½√3i). Ecco un'ulteriore novità: la somma di un numero reale e uno immaginario dà luogo a un oggetto che si chiama "numero complesso". Finalmente, possiamo affermare che i
numeri complessi sono l'ultima classe di cui ci sia bisogno in matematica: non è mai stata trovato un altro tipo di operazioni che richieda un'ulteriore estensione del concetto di numero!
▲ Il Piano ComplessoI numeri reali possono essere raffigurati su una retta, in modo che numeri più grandi stiano sempre alla destra di numeri più piccoli:
(in rosso i numeri interi, in verde i razionali, in blu irrazionali).Come abbiamo visto, i numeri complessi sono invece espressi da due quantità, una reale e l'altra immaginaria. Non è quindi sufficiente una retta per rappresentarli in modo geometrico, ci vuole un piano: si definisce "piano complesso" un piano cartesiano in cui l'asse orizzontale indica la parte reale e l'asse verticale la parte immaginaria di ogni numero complesso. Faccio un esempio proprio con una le radici cubiche di 1, di cui abbiamo parlato sopra:
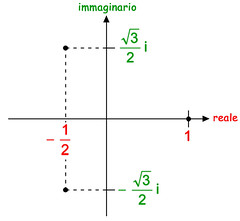Ciascun punto è identificato da due coordinate: quella che "cade" sull'asse orizzontale (numero reale, indicato in rosso) e quello che cade sull'asse verticale (parte immaginaria, indicata in verde; la lettera i l'ho messa per chiarezza, anche se non andrebbe scritta in quanto implicita nell'asse verticale, che definisce appunto la parte immaginaria del numero complesso).Se ci fate caso, queste tre radici 1 si dispongono sul piano complesso come i vertici di un triangolo equilatero inscritto in una circonferenza unitaria:
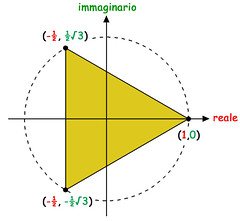Qui le coordinate di ciascun punto sono indicate come coppie di numeri fra parentesi, separati da virgole. Il primo numero (rosso) definisce la parte reale, il secondo (verde) la parte immaginaria del numero complesso che definisce ciascun vertice.Lo stesso accade anche con le radici quarte:
▲ 
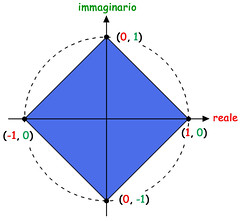L'Equazione Ciclotomica"L'equazione ciclotomica consiste nel trovare tutte le radici dell'unità nel piano complesso. Tale equazione può essere espressa in due modi assolutamente equivalenti:
zⁿ = – 1 = 0 zⁿ = 1
in cui z è un numero complesso che rappresenta la radice dell'unità, n il grado dell'equazione.
Si dimostra (con metodi matematici di gran lunga troppo complicati per essere spiegati qui), che le le radici di 1, calcolate in qualsiasi grado, sono sempre nello stesso numero del grado della radice; e, se disegnate sul piano complesso, queste radici si dispongono secondo i vertici di un poligono regolare di tanti lati quanto è il grado della radice: da qui il nome di equazione "ciclotomica", ovvero equazione che "taglia il cerchio". Ecco rappresentate qui le radici di quinto grado:
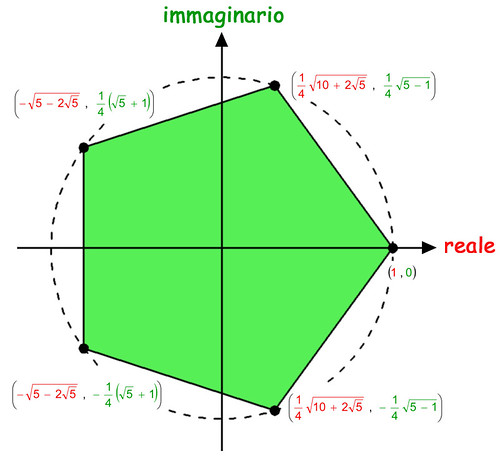
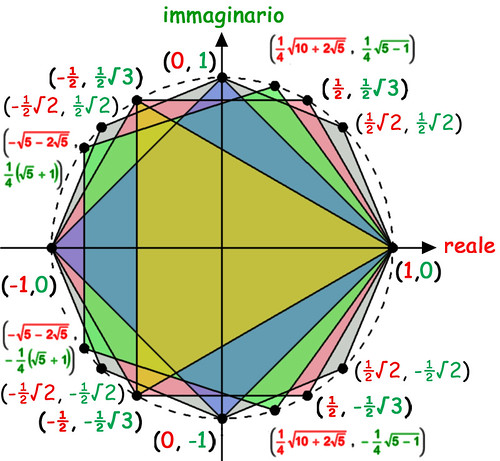
Bene, per chi volesse verificarle, qui sotto do le coordinate di tutti i vertici del triangolo, quadrato, pentagono, esagono e ottagono regolari inscritti nella circonferenza di raggio unitario: buon lavoro!
▲ 
Niccolò Tartaglia
Targa commemorativa di Niccolò Tartaglia in piazza Paolo VI (ex piazza Duomo) a Brescia, sullo stipite della porta principale del Duomo Vecchio (o "Rotonda").Durante la presa di Brescia da parte dei francesi nel 1512, Niccolò Fontana (Brescia, 1499 circa – Venezia, 13 dicembre 1557) fu ferito alla mandibola e al palato. Sopravvisse a stento a queste ferite, rimanendo segnato per tutta la vita da una evidente difficoltà ad articolare le parole. Per questo ebbe il soprannome di "Tartaglia", soprannome che usò lui stesso tutta la vita per firmare le proprie opere.
Fu matematico sommo, e il suo nome è legato ad alcune cose davvero notevoli:
— fu il primo traduttore in lingua italiana degli "elementi" di Euclide
— descrisse per primo in occidente il celebre triangolo che porta il suo nome (era già noto in Cina da almeno due secoli).
— scoprì la formula risolutiva delle equazioni cubiche. Ecco la storia di questa scoperta:
La formula risolutiva per le equazioni cubiche fu scoperta per primo da Scipione dal Ferro, cosa non facile in tempi in cui non erano ancora stati affrontati i numeri negativi né tanto meno i numeri immaginari. A quei tempi i matematici custodivano gelosamente le loro scoperte, infatti i risultati di dal Ferro non furono pubblicati, ma andarono in "eredità" ad Antonio Maria del Fiore, un suo non brillantissimo discepolo. Quest'ultimo iniziò a vantarsi della propria capacità di risolvere equazioni cubiche; il Tartaglia lo venne a sapere, si mise a studiare il problema e raggiunse gli stessi risultati: a quel punto accettò un "cartello di matematica disfida" da parte di del Fiore.
In queste disfide pubbliche ciascuno dei contendenti sottoponeva all'altro una serie di problemi, poi una giuria scelta di comune accordo decretava il vincitore. In quest'occasione il Tartaglia risolse tutti i problemi sottopostigli da del Fiore in un paio d'ore, mentre il del Fiore non riuscì a risolvere alcuno dei problemi proposti dal Tartaglia.
Dell'esito di questa disfida venne a conoscenza Gerolamo Cardano (quello del giunto cardanico), che invitò il Tartaglia a Milano e riuscì a farsi confidare la formula dietro la promessa che non sarebbe stata divulgata. Passarono gli anni, e il Tartaglia non si decideva a pubblicare la formula; nel contempo il Cardano non solo la migliorò, ma venne anche a sapere dei risultati di Scipione dal Ferro: a questo punto, un po' perché nella formula ci aveva messo anche del suo, un po' perché appunto scoprì che i risultati del Tartaglia erano già stati trovati da qualcun altro, il Cardano si sentì svincolato dalla promessa fatta, e incluse la famosa formula nella sua "Ars Magna" del 1545.
Il Tartaglia non la prese bene, e ne nacque una disputa a tratti molto aspra, che sfociò in una serie di "disfide" lanciategli da Ludovico Ferrari, un allievo del Cardano. Il Tartaglia, vista la sua menomazione, avrebbe voluto svolgere le disfide per iscritto, ma gli fu invece imposto di sostenere gli scontri in modo orale. Nell'ultima di queste disfide, al Tartaglia fu addirittura impedito di esporre le proprie ragioni... sicché il poveretto ne uscì con il prestigio infangato, perse il lavoro ed ebbe grossi problemi finanziari per tutto il resto dei suoi giorni!
La formula risolutiva dell'equazione cubica porta oggi il nome di formula Cardano-Tartaglia.
▲ Prossimo capitolo: Elevamento a potenza
