Aritmetica: Sistemi di numerazione

Sommario:

+ Contare
– Sistemi di numerazione
      Numeri Romani
      Numeri Babilonesi
      Numeri Decimali
      Numeri Binari
+ Addizione e Sottrazione
+ Moltiplicazione
+ Divisione
+ Radice Quadrata
+ Elevamento a potenza
+ Logaritmi
+ Il Regolo Calcolatore

Nel capitolo precedente abbiamo visto come l'operazione del contare sia sufficiente a risolvere molti problemi aritmetici. Ovviamente quando i numeri da trattare diventano troppo grandi bisogna trovare qualche sistema più veloce; ma se i numeri diventano troppo grandi... bisogna trovare anche il modo di scriverli! Infatti non si può pensare di andare avanti a lungo facendo solo dei segni tutti uguali:



Numeri Romani

I romani decisero di raggruppare le tacche a gruppi di cinque con l'adozione del segno V. La leggenda vuole che sia un segno che rappresenta una mano aperta:



così come la X, per il numero 10, rappresenterebbe due mani insieme:



la cosa più probabile è comunque che tali segni siano stati scelti perché facili da intagliare su un palo di legno; in effetti sono stati trovati esempi di numeri scritti con simboli diversi da quelli "moderni", e l'adozione di lettere tutte facenti parte dell'alfabeto latino è stato un processo piuttosto lungo. Per esempio:



il 50 era nato come una V con una tacca in più (sempre un simbolo facile da intagliare); nel tempo è evoluto fino a diventare la L che conosciamo. Analogamente:



il 100 è nato come una X con una tacca in più, poi si è evoluta fino ad assumere la forma della lettera C (forse dal latino "centium").

Alla fine era stata codificata una forma standard di rappresentare i "numeri base", in modo da arrivare fino al milione:



Il problema con questi numeri era che, per quanto apparentemente intuitivi, era molto difficile di farci i calcoli.   ▲  

Numeri Babilonesi

Mentre i romani, che non erano grandi scienziati, si "accontentavano" di questi numeri, le civiltà vicine adottavano sistemi di gran lunga migliori, come quelli greco, egizio e soprattutto babilonese:



Quella riprodotta nella foto è una tavoletta babilonese in argilla trovata nel XIX secolo, la cosiddetta tavoletta Plimpton 322 (dal nome della collezione di G.A. Plimpton presso la Columbia University).

Risalente al 1800 a.C. circa, contiene numeri in scrittura cuneiforme disposti in una tabella di quattro colonne per 15 righe. Secondo una delle interpretazioni, i numeri sono un elenco di terne pitagoriche i cui numeri sono le soluzioni del teorema di Pitagora, a² + b² = c², (per esempio 3² + 4² = 9 + 16 = 25 = 5²), ma posti in un modo tale da dar luogo a una serie di valori trigonometrici!

I babilonesi costruiscono un sistema di numerazione davvero geniale: utilizzano per la prima volta un sistema posizionale per cui un ristretto numero di simboli cambia significato in base alla loro posizione reciproca. La cosa per noi oggi è evidente: se scrivo il numero 2222, vuol dire che sto sommando due migliaia con due centinaia con due decine con due unità: totale 2222, appunto, in cui la cifra 2 assume quattro significati diversi.

La cosa notevole è che, a differenza di tutti gli altri sistemi sviluppati nella storia e che sono basati sui numeri 5 e 10 (dalle dita delle nostre mani), e talvolta sul numero 20 (anche quelle dei piedi...), i babilonesi scrivono i loro numeri basandosi sul numero 60. Insomma inventano un sistema di scrittura dei numeri in base 60: usando 59 simboli, da 1 a 59 (più il simbolo su sfondo verde, di cui parlerò fra poco):



erano in grado di scrivere la cifra delle unità (da 1 a 59 appunto), delle "decine" (in realtà a ogni unità della seconda cifra corrispondeva il valore 60), delle "centinaia" (a ogni unità della terza cifra corrispondeva il valore 3600) e così via. Non solo: scrivevano anche i numeri decimali, usando gli stessi simboli per i sessantesimi, poi i tremilaseicentesimi... Faccio un esempio:



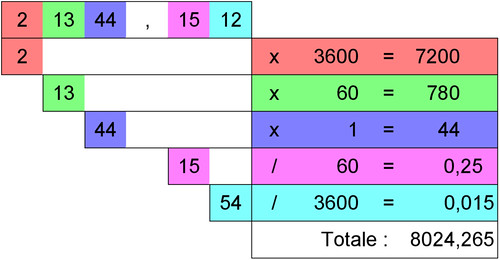
Come potete vedere dai conti, il numero 2 13 44 , 15 12 voleva dire 8024,265. A noi sembra astruso... ma è solo questione di abitudine: forse ai babilonesi sarebbe sembrato astruso il nostro sistema decimale!

A proposito: perché usare proprio il numero sessanta? Forse perché ha molti divisori: il 60 può essere diviso per 2 e per 5 (come il nostro 10), ma anche per 3, 6, 12, 15, 20 e 30, quindi i babilonesi avevano molte più probabilità di noi di scrivere numeri decimali esatti (per noi anche la semplice divisione 1 : 3 dà infiniti decimali).

Nel corso dei secoli i babilonesi si sono accorti che la mancanza di un simbolo per lo zero creava confusione: di solito si doveva capire dal discorso se un numero di due cifre rappresentava unità e "decine" (sessantine) o unità e "centinaia" (tremilaseicentine). Infatti a un certo punto viene creato anche il simbolo per lo zero (quello su sfondo verde nell'immagine delle cifre qui sopra); ma non c'è da farsi ingannare: si tratta dello zero come cifra, non come numero! Infatti un conto è usare un simbolo che ha solo funzione di "segnaposto" (come nel numero 101, che vuol dire: un centinaio, nessuna decina e una unità); un altro conto è concepire un numero completamente nullo: per abituarsi a concepire lo zero come numero (che infatti non è un numero naturale) bisogna aspettare la metà del XVI secolo!

Claudio Tolomeo (circa 100-175), l'autore del famoso Almagesto (il libro in cui descrive il sistema geocentrico)utilizza in tutta la sua mirabile opera proprio questa notazione numerica, la più versatile di quelle allora conosciute. Per di più si verificava una coincidenza clamorosa relativamente al pi-greco:



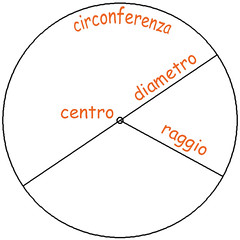
Per definizione π è il rapporto fra circonferenza e diametro di un cerchio; e da quando l'uomo si è messo a studiare la geometria ha cercato di determinarne il valore con la massima precisione possibile. Su π sono stati scritti libri interi, e per la determinazione della sua natura di numero (il famoso problema della "quadratura del cerchio") si è dovuto attendere la fine del XIX secolo! Ai tempi di Tolomeo ne era stata trovata una buona approssimazione nella frazione 377 / 120: il quoziente della divisione 377 : 120 dà 3,1416 con 6 periodico, un'ottima approssimazione di π (che in realtà vale 3,14159265...), con un errore di solo 0,000074 (precisione addirittura dello 0,002%). Per Tolomeo deve essere stato ovvio scegliere il valore 60 per il raggio della circonferenza trigonometrica in base alla quale fare tutti i suoi calcoli: non solo era la base della numerazione da lui impiegata, ma con il suo doppio otteneva 120, cioè il diametro di un bellissimo cerchio la cui circonferenza è (quasi) esattamente un numero intero, ovvero 377! (il calcolo esatto sarebbe 376,991)

(Per completezza, c'è da dire che 355 : 113 dà π con una precisione oltre 250 volte migliore rispetto a 377 : 120; ma di questa frazione con il 113 al denominatore non ho mai trovato traccia da nessuna parte)

Una numerazione basata sul 60 ci può sembrare strana, ma i numeri babilonesi hanno lasciato un'eredità che è ancora viva: sui nostri orologi, con le ore che si dividono in sessanta minuti di sessanta secondi; e negli angoli, in cui ogni grado si divide in 60 primi di 60 secondi.   ▲  

Numeri Decimali

In Europa per molti secoli rimasero in uso solo i numeri Romani; e le cose peggiorarono ulteriormente nei secoli bui del medioevo, quando diventò mentalità corrente che lo studio si dovesse applicare solo alla teologia e alla filosofia: le scienze "esatte" furono accantonate quasi del tutto. Nel frattempo il sistema posizionale babilonese veniva adottato in India, cambiando da sessagesimale a decimale e dando luogo a ciò che oggi chiamiamo numeri indiani, o indo-arabici, o arabi (insomma, i numeri che conosciamo oggi).

Insomma in Europa i numeri romani continuarono ad essere utilizzati per fare i conti, in quanto nella vita quotidiana, senza problemi scientifici da risolvere, non è frequente dover fare cose più complicate che somme e sottrazioni. A meno che...



... uno non dovesse gestire un banco di cambiavalute! Questo mestiere richiedeva di dominare concetti come frazioni, decimali, moltiplicazioni e divisioni (tutti argomenti di cui mi occuperò prossimamente); e qui i numeri romani sono un disastro: per fare i calcoli era indispensabile ricorrere all'abaco (di cui parlerò a partire dal prossimo capitolo).

La svolta avviene all'inizio del 1200 a opera di Leonardo da Pisa, detto Fibonacci (filius Bonacii, 1170-1250). Visse alcuni anni assieme al padre Guglielmo dei Bonacci, che era rappresentante dei mercanti della Repubblica di Pisa nella regione di Bugia (Algeria), dove studiò i procedimenti aritmetici che gli studiosi musulmani stavano diffondendo nelle varie regioni del mondo islamico. Qui ebbe anche contatti con il mondo dei mercanti e con tecniche matematiche sconosciute in Occidente. Alcuni di tali procedimenti erano stati introdotti per la prima volta in India: proprio per perfezionare queste conoscenze, Fibonacci viaggiò molto, arrivando fino a Costantinopoli, alternando il commercio con gli studi matematici.

Nel 1202 Fibonacci scrive un testo fondamentale per la cultura occidentale: il "Liber Abaci", un ponderoso manuale di aritmetica e algebra, con il quale introduce in Europa il sistema numerico decimale indo-arabico e i principali metodi di calcolo relativi. L'innovazione cruciale è la seguente:

Ci sono nove figure degli indiani: 9 8 7 6 5 4 3 2 1. Con queste nove figure, e con il simbolo 0, che gli arabi chiamano zephiro [da cui poi il nome "zero"], qualsiasi numero può essere scritto, come dimostreremo.

In questo libro Fibonacci spiega i fondamenti della nuova numerazione, insegnando gli algoritmi per calcolare le quattro operazioni senza dover ricorrere all'abaco; è a partire da qui che si sviluppano l'aritmetica, l'algebra e la matematica in occidente.

Un'altra storia da raccontare sarebbe l'evoluzione dei simboli adottati per scrivere le varie cifre; infatti anche al giorno d'oggi le cifre utilizzate nel mondo arabo sono molto diverse dalle nostre:



In realtà il metodo numerico indiano era arrivato in occidente già il secolo precedente, ad opera del traduttore, filosofo e matematico britannico Adelardo di Bath (1080-1152). Adelardo tradusse in latino il libro "Algoritmi de numero Indorum" del matematico persiano Al-Khwarizmi (nome completo Abu Ja'far Muhammad ibn Musa Khwarizmi, 780-850 circa). La prima parola del titolo è una traslitterazione del nome; ma in seguito si è persa l'origine di nome proprio e la parola algoritmo è diventata un sostantivo comune, assumendo il significato (anche in informatica) di metodo standard per compiere un compito complesso in base a procedimenti elementari (somma le cifre, scrivi il risultato, riporta il riporto, somma...).

La traduzione di Adelardo, sebbene abbia preceduto l'opera di Fibonacci, non ebbe molto successo. Fibonacci fu più fortunato, forse anche perché il Liber Abaci veniva scritto in una Toscana dedita a traffici di tutti i generi... dove questo nuovo sistema ha trovato subito un certo numero di estimatori. Attenzione però: le abitudini sono dure a morire, e coloro che non avevano bisogno di compiere calcoli complicati continuarono a utilizzare i numeri romani ancora per secoli!   ▲  

Numeri Binari

Tutti i sistemi di numerazione che abbiamo visto più sopra sono di fatto equivalenti: in qualche modo consentono di scrivere gli stessi numeri (almeno, i numeri interi). Quindi la scelta del sistema di numerazione viene fatta in base alla sua praticità: ed ecco che, per certi usi, neanche il sistema decimale è il più adatto.

Da quando è stata utilizzata l'elettricità per fare i calcoli (attraverso relè, valvole, transistor o microprocessori) ogni circuito si può trovare in due stati diversi: acceso e spento. A questi due stati vengono associati i simboli 0 e 1: ecco la nascita del sistema binario!

Il quale funziona esattamente come quello decimale; solo che invece di funzionare per potenze di 10 (decine, centinaia, migliaia) funziona per potenze di 2. Quindi:

1011 = 1 x 2³ + 0 x 2² + 1 x 2¹ + 1 x 2° = 8 + 0 + 2 + 1 = 11

I programmatori di computer sono abituatissimi a fare calcoli di vario generi su numeri come questi; ma quando i numeri diventano molto grandi la cosa non è molto pratica. Infatti per esprimere il numero (decimale) 1234567 occorre il seguente numero (binario):

1234567 (d) = 100101101011010000111 (b)

Per semplificare la scrittura di questi numeri grandi sono stati "inventati" altri due sistemi di numerazione:

— Ottale, in cui vengono raggruppate le cifre binarie a gruppi di tre, quindi codificando le cifre da 0 a 7.

1234567 (d) = 4553207 (o)

— Esadecimale, in cui vengono raggruppate le cifre binarie a gruppi di quattro. In questo caso i valori che può assumere ciascuna cifra vanno da 0 a 15: a ogni cifra quindi viene assegnato un simbolo che va da 0 a 9 o da A ad F.

1234567 (d) = 12D687 (h)   ▲  

Prossimo capitolo: Addizione e sottrazione