Aritmetica: i Logaritmi

Sommario:

+ Contare
+ Sistemi di numerazione
+ Addizione e Sottrazione
+ Moltiplicazione
+ Divisione
+ Radice Quadrata
+ Elevamento a potenza
– Logaritmi
      John Napier
      Ricerca di una Base
      Proprietà dei logaritmi
      Logaritmi decimali, o di Briggs
      Esempi di calcolo con i logaritmi
      I logaritmi "Naturali"
      Usi "quotidiani" dei logaritmi (deciBel, pH...)
      Conclusioni, e una "perla" letteraria
+ Il Regolo Calcolatore

I logaritmi non fanno parte dell'aritmetica, ma sono una diretta conseguenza dell'elevazione a potenza di cui ho parlato nel capitolo precedente.

John Napier



Il protagonista di questa storia è lo scozzese John Napier (italianizzato Nepero, 1550-1617). Non era un matematico di professione, bensì un ricco proprietario terriero di nobile famiglia, con vasti interessi che andavano dall'astrologia all'alchimia, dalla teologia (era un convinto anti-papista) alla matematica. Le malelingue insinuavano che si desse anche alla magia nera e frequentasse il diavolo... ma questa era un'accusa piuttosto comune, a quei tempi!

Sentiva in modo particolare la necessità di trovare un sistema per velocizzare i calcoli aritmetici. A questo riguardo scrisse:

Eseguire calcoli è operazione difficile e lenta, e spesso la noia che ne deriva è la causa principale della disaffezione che la maggioranza della gente prova nei confronti della matematica...

A proposito dei calcoli, nel 1617 fu stampato (postumo) il libro in cui descrive l'uso dei cosiddetti bastoncini o ossi di Nepero (dall'inglese Napier's Bones), con i quali ho già descritto il modo di calcolare moltiplicazioni, divisioni e radici quadrate. L'impegno di Nepero in matematica però non si esaurisce qui: infatti fornirà al mondo qualcosa di davvero rivoluzionario!

Partendo dalle proprietà delle potenze (di cui parlo qui), e in particolare dal fatto che

Il prodotto di due potenze che hanno la stessa base è uguale a un'unica potenza con esponente pari alla somma degli esponenti delle due potenze di partenza

iniziò a studiare la possibilità di trasformare prodotti (delle potenze) in somme (degli esponenti). Negli anni in cui si occupava di questo argomento, tramite il fisico scozzese John Craig suo amico, entrò in contatto con l'ambiente scientifico di Tycho Brahe e venne a sapere del nuovo procedimento di calcolo delle moltiplicazioni con il metodo di prostaferesi (ne parlo qui). Questi contatti gli dettero ulteriori stimoli a proseguire con le sue ricerche... per cui cominciamo a vedere di cosa si trattava!   ▲  

Ricerca di una Base

Il lavoro di Nepero si basa una semplice intuizione. Se devo moltiplicare diecimila per un milione posso fare:



passando dai numeri alle loro potenze di dieci, sommando gli esponenti, e alla fine calcolando la potenza di dieci con il nuovo esponente.

L'uso di soli esponenti interi non è certo di molta utilità. Nepero provò allora a usare esponenti decimali, facendo delle semplici proporzioni: se 100 sta a 1000 (fattori da moltiplicare) come 2 sta a 3 (esponenti), non è che al numero 550 (la media aritmetica fra 100 e 1000) potrebbe corrispondere l'esponente 2,5 (media aritmetica fra 2 e 3)? Se così fosse si sarebbe potuto fare:



ma evidentemente il risultato della potenza (rosso) e del prodotto calcolato in modo normale (verde) non coincidono. Facendo molti tentativi, Nepero si accorse che le cose miglioravano sensibilmente usando basi sempre più vicine all'unità. Alla fine optò per questa base:



Vediamo cosa succede. Ammettiamo di conoscere i valori delle seguenti potenze (in rosso alcuni numeri che serviranno fra poco):



Se proviamo a calcolare il valore per l'esponente 3 come media di quelli del 2 e del 4 otteniamo



che è praticamente identico al valore reale:



Facciamo una riprova con la moltiplicazione 0,9999998 x 0,9999997 utilizzando questi numeri, che indico con gli stessi colori rosso e verde che ho usato sopra:



Il valore trovato è praticamente esatto, infatti calcolando il prodotto e non la potenza della somma degli esponenti, si trova un numero quasi identico:



Nepero scoprì quindi di essere sulla buona strada; solo non gli piacevano tutte quelle cifre dopo la virgola: quindi moltiplicò tutti i suoi esponenti per 10000000. I numeri calcolati sopra quindi diventano:



Per ora sembra che il risultato sia "lineare", cioè che al crescere dell'esponente decresca in pari misura anche la potenza, ma non è sempre così. Vediamo per valori più alti:



Ecco che gli intervalli fra gli esponenti non sono più proporzionali alle differenze fra i numeri sulla sinistra.

Ora riporto altri tre numeri, giusto per fare un calcolo di prova:



Proviamo a calcolare il seguente prodotto:



Il calcolo reale sarebbe:



Mancano 7 cifre all'appello! Ma questo è naturale: siccome i numeri di Nepero sono stati tutti moltiplicati per 10000000, c'è proprio questa discrepanza nel risultato. Allora il calcolo di Nepero va aggiornato:



il risultato finale differisce pochissimo dal risultato effettivo, calcolato a mano!   ▲  

Proprietà dei logaritmi

Dopo una ventina d'anni di duro lavoro, nel 1614 Nepero pubblicò il Mirifici Logarithmorum Canonis Descriptio in cui spiega il funzionamento (57 pagine) e fornisce le tavole (90 pagine!) di questi suoi Logaritmi (il termine deriva dalle parole greche logos, nel senso di proporzione, e arithmos, numero). Vediamo ora gli aspetti pratici di questo sistema.

Il discorso è relativamente semplice: se una volta scelto un numero fisso da usare come base calcolo tutte le potenze di quella base, posso costruire una tabella per cui a ogni esponente corrisponde un numero pari al risultato dell'elevamento a potenza di quella base a quell'esponente. Si definisce quindi:

Logaritmo in base a di un numero x è
l'esponente da dare ad a per ottenere x
(x viene chiamato "argomento" del logaritmo).

per vedere un po' meglio di cosa si tratta partiamo da due numeri (arg) e dai loro logaritmi (log):



Se tramite una tabella riesco a conoscere i valori degli esponenti, ovvero i logaritmi dei due argomenti, allora per fare la moltiplicazione di questi due argomenti (fattori) posso procedere così:



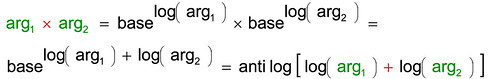
Il procedimento è estremamente più semplice di una moltiplicazione: per farla basta consultare due volte le tabelle, fare una semplice somma e poi consultare "all'indietro".

Non solo: a differenza del metodo di prostaferesi, con il quale si possono fare solo moltiplicazioni, con i logaritmi si possono fare anche divisioni:



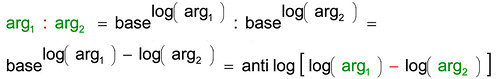
estrazioni delle radici di ogni grado:



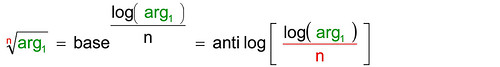
e tante altre belle operazioni!   ▲  

Logaritmi decimali, o di Briggs

Non c'è da stupirsi che questo nuovo metodo di calcolo abbia avuto immediato riconoscimento nell'ambiente scientifico dell'epoca. Fra gli ammiratori più entusiasti c'era Henry Briggs (1561-1630), che nel 1615 si recò da Nepero per discuterne possibili modifiche alle sue tabelle. Si accordarono su una nuova impostazione (che accennerò fra pochissimo), che avrebbe richiesto di ricalcolare tutte le tavole numeriche! Vista l'età ormai avanzata di Nepero, il compito ricadde sul Briggs, che fece un lavoro enorme: calcolò più di 30000 logaritmi fino alla quattordicesima cifra decimale dopo la virgola... e questo fu solo l'inizio, in quanto pubblicò anche tabelle dei logaritmi dei seni, coseni, tangenti, insomma fece un lavoro enorme!

Il nuovo sistema di Briggs dei logaritmi decimali (o volgari, o di Briggs) si fonda sulla base 10, per cui:



I valori intermedi si calcolano in vari modi. Per esempio si sa che, fra le proprietà delle potenze, c'è quella per cui l'elevamento all'esponente 1/2 significa estrarre la radice quadrata della base. Quindi calcolando a mano la radice quadrata di 10 si ottiene:



Con metodi complicati, ma anche ingegnosi, e sfruttando tutte le scorciatoie e semplificazioni possibili, nel 1617 Briggs pubblicò la prima tavola dei logaritmi dei numeri da 1 a 1000. I risultati successivi, di cui ho accennato sopra, sono del 1624.   ▲  

Esempi di calcolo con i logaritmi

Quando frequentavo le superiori, verso il 1975, le calcolatrici elettroniche cominciavano appena a diffondersi; quindi i programmi scolastici prevedevano l’insegnamento del calcolo con le tabelle dei logaritmi, che comparivano su appositi libri di tavole numeriche. Ora è ovvio che disponendo di una tabella in due colonne, in cui a sinistra ho un numero e a destra il suo logaritmo, la stessa tabella si presta a ricavare l'antilogaritmo: basta cercare il logaritmo nella colonna di destra e trovare il numero corrispondente nella colonna di sinistra.

I logaritmi vengono divisi tecnicamente in due parti: caratteristica e mantissa. La caratteristica indica l'ordine di grandezza del numero: a numeri con una sola cifra intera corrisponde caratteristica 0; a 3 cifre intere caratteristica 2; a 4 zeri dopo la virgola -5. Infatti:



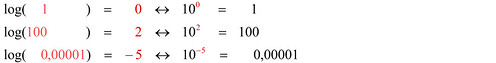
Abbiamo detto che i logaritmi sono esponenti; sappiamo inoltre che al prodotto di due potenze corrisponde la somma degli esponenti. Ogni numero può sempre espresso dal prodotto di due numeri, di cui uno esprime l'ordine di grandezza (1 10 100... oppure 0,1 0,01 0,001...) e l'altro un numero con una sola cifra intera e tutti gli altri decimali. Ciascuno di questi due numeri avrà un suo logaritmo, di cui il primo sarà sempre un numero intero (come mostrato nella tabella sopra), mentre l'altro sarà sempre uno zero virgola qualcosa (avendo questo secondo numero una sola cifra intera): il logaritmo di questo secondo numero si chiama mantissa.

Se andiamo a vedere le tabelle dei logaritmi, queste non presentano neanche la virgola negli argomenti: i numeri 7, 70, 700 e così vengono implicitamente ricondotti al numero 7,000. Qui sotto indico in verde le cifre significative del numero, e la mantissa del suo logaritmo:



Vediamo allora come si ottiene il valore completo dei logaritmi. Dicevamo che il logaritmo del prodotto è uguale alla somma dei logaritmi, quindi si considerano separatamente l'ordine di grandezza e le cifre significative. Per esempio il numero 700 ha caratteristica 2 (in rosso) e mantissa 0,8451 (in verde):



Nella riga inferiore mi occupo invece di un numero più piccolo dell'unità: il procedimento è lo stesso, ma si presenta una complicazione in più: siccome il logaritmo sarà negativo, la parte decimale diventa il complemento della mantissa; in pratica il 0,8451 diventa 0,1549 (in grigio, a destra). Per ovviare a questo problema (soprattutto per evitare probabili errori) i logaritmi minori di zero si indicano in modo diverso:



La mantissa rimane invariata, e il -5 della caratteristica viene indicato come un 5 con una lineetta sopra. In questo modo il logaritmo rimane "positivo", ma bisogna considerare che la caratteristica (la sola parte intera) in realtà è negativa.

Proviamo ora a fare dei calcoli con questi numeri:



Nei calcoli che seguono, i numeri in grigio sono i logaritmi; in verde i valori reali delle varie operazioni, in rosso i valori calcolati tramite i logaritmi:



Considerando che ho utilizzato logaritmi con solo 4 cifre di mantissa, non c'è davvero male!   ▲  

I logaritmi "Naturali"

I logaritmi Naturali o Neperiani sono costruiti su una base diversa dal 10 di Briggs; la base è un numero che si identifica con la lettera e:



il quale si ottiene calcolando la seguente espressione:



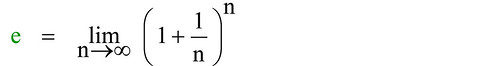
Questa espressione ci dice che il numero e va calcolato (semplifico!) elevando all'infinitesima potenza un numero che è di un infinitesimo più grande dell'unità! Il risultato è quello che ho scritto sopra: fidatevi.

E da dove salta fuori questo strano numero? La "colpa" è di Leonhard Euler (detto Eulero in italiano, 1707-1783), che è stato uno dei massimi matematici mai esistiti (è uno dei tre cosiddetti principi della matematica assieme ad Archimede di Siracusa e a Gauss, con cui abbiamo già avuto a che fare in questa storia dell'aritmetica). Eulero ha dato un contributo fondamentale all’analisi matematica che è quella parte della matematica che si occupa di derivate, integrali ed equazioni differenziali. Lui scoprì che questo numero infernale saltava fuori da tutte le parti; in matematica è altrettanto fondamentale quanto il pi greco, che lega il diametro alla circonferenza del cerchio. A proposito di pi greco: fu proprio Eulero a "battezzare" i seguenti numeri:

— π (pi greco): non ci crederete, ma c’è voluto il diciottesimo secolo per dare il nome definitivo a questo numero conosciuto fino dall’antichità. Pare che Eulero, attribuendogli questa lettera greca, volesse rendere omaggio ad Archimede.

— i (la lettera i minuscola): il valore della radice quadrata di -1, ossia l’unità immaginaria (di cui parlo qui).

— e (la lettera e minuscola): il numero di cui stiamo parlando. Qui pare che la magnanimità di Eulero sia stata un po’ meno marcata, in quanto questa "e" assomiglia molto all’iniziale del suo cognome...

Ma cosa c'entra questo numero e con Nepero? Rivediamo la sua formula dei logaritmi:



Se facciamo una moltiplicazione e una divisione per 10000000 (numeri in verde) otteniamo l'espressione di destra, che è una nuova formula per il calcolo dei logaritmi derivata direttamente da quella di Nepero.



Insomma la parte rossa dell'espressione sopra, che riporto qui di seguito per chiarezza



assomiglia moltissimo a quest'altra espressione:



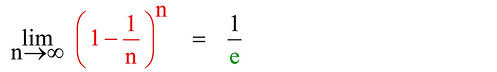
Il cambio di segno dentro la parentesi ha comportato di ottenere 1/e invece di e; per il resto, Nepero non ha utilizzato un valore n infinito, ma si è "limitato" al valore 10000000, che è già "abbastanza" grande da dare risultati soddisfacenti.

Nepero, senza saperlo, aveva inventato una base per i suoi logaritmi strutturalmente simile al valore e di Eulero: per questo si ascrive a Nepero la paternità del numero, e si dicono Neperiani i logaritmi calcolati con questa base. Certo è che Nepero non poté neanche sospettare l’importanza che avrebbe avuto questo numero nell’analisi...   ▲  

Usi "quotidiani" dei logaritmi

Forse non lo sapete, ma le scale che misurano i seguenti fenomeni:

— La magnitudo delle stelle (indice della loro luminosità);

— L'indice pH di attività dello ione idrogeno (misura dell'acidità);

— La scala Richter (misura dell'intensità dei terremoti);

— i decibel che misurano l'intensità delle onde sonore;

sono tutte scale logaritmiche, ovvero misurano il logaritmo del rapporto fra ciò che viene misurato e un valore standard preso come riferimento. Vediamo queste scale da vicino.

La moderna scala delle magnitudini è stata scelta in modo che (semplificando), scelta una stella molto luminosa a cui dare magnitudo 0 (è stata scelta Vega, nella costellazione della Lira), la magnitudo 5 corrisponda a una luminosità 100 volte inferiore. Detto in formula:



in cui il segno meno fa sì che la magnitudo aumenti quando la stella è meno luminosa; M è la magnitudo calcolata; F è il flusso di luce della stella che stiamo osservando; V è la luminosità di Vega; e il valore 2,5 serve per far sì che una stella 100 volte meno luminosa di Vega abbia proprio magnitudo 5.

Con questo modo di indicare la luminosità delle stelle, è sicuramente più facile dire che la massima luminosità di Plutone è di magnitudo 13,65, piuttosto che dire che Plutone ha una luminosità duecentottantottomilaquattrocento (288400) volte inferiore a Vega!

In televisione non c'è pubblicità di cosmetici che non tenga a farci sapere il pH delle varie creme... ma alzi la mano chi sa esattamente cosa sia il pH!

Il pH fu ideato dal chimico danese Søren P. L. Sørensen nel 1909, il quale stava affrontando alcuni problemi relativi al processo di fermentazione della birra. Questo processo richiede un controllo molto accurato dell'acidità dei mosti, la quale, a quel tempo, veniva espressa attraverso la concentrazione degli ioni idrogeno presenti in soluzione. Questi ioni, normalmente, sono in quantità molto piccola, anche inferiori a una parte per milione. Sørensen si rese conto che i calcoli si sarebbero di molto semplificati facendo riferimento al solo esponente del valore della concentrazione, anziché a tutto il numero. Propose quindi di chiamare questo esponente pH, dove p sta per potenza (cioè esponente del 10, dal latino pondus) e H sta per idrogeno, o meglio, per ione idrogeno, (dal latino Hydrogenii).

Oggi, il pH viene definito come l'opposto del logaritmo della concentrazione molare degli ioni idrogeno. Pertanto:



La concentrazione suddetta permette di definire il grado di acidità o basicità della soluzione. Il pH può assumere valori appartenenti all’intervallo 1-14; ma siccome stiamo parlando di logaritmi, fra il valore 1 e il valore 14 ci sono 13 cifre, o posizioni decimali, di differenza!

Risulta quindi molto più facile esprimersi in termini di pH rispetto all'effettiva concentrazione dello ione idrogeno; e si hanno soluzioni acide se il loro pH è compreso fra 1 e 6, neutre se il valore è 7 (come l'acqua distillata), basica fra 8 e 14.

Anche la magnitudo dei terremoti, così come indicata dalla scala Richter, ha a che fare con i logaritmi. Tale scala si basa sulla potenza equivalente del sisma, misurata in chili di tritolo. Quindi la magnitudo 0 equivale a un chilo di tritolo; poi ogni salto di due magnitudo equivale a moltiplicare la quantità di tritolo per 1000:



Anche in questo caso è più facile dire "Terremoto del sesto grado della scala Richter", piuttosto che "sisma dalla potenza equivalente a un milione di tonnellate di tritolo"!

Il Bel è il logaritmo decimale del rapporto fra due potenze; il decibel (dB) è lo stesso valore, ma moltiplicato per 10. Quindi:



in cui w2 è l'intensità sonora misurata, mentre w1 è l'intensità di riferimento standard. Quest'ultima è stabilita come il livello minimo di potenza sonora che sia percepibile dall’orecchio umano. Quindi se la potenza da misurare W2 è uguale a quella di riferimento, allora il rapporto W2/W1 è uguale a 1, e il logaritmo è 0. Se la potenza fosse cento volte superiore a quella di riferimento, il logaritmo varrebbe 2, quindi i dB di potenza sarebbero 20.

I decibel sono molto pratici proprio perché una variazione di 10dB comporta un aumento della potenza di 10 volte, mentre a un raddoppio di potenza corrispondono circa 3dB. E tutto questo è molto più pratico che esprimersi in termini lineari (cioè non logaritmici): per esempio a 43dB corrisponderebbe una potenza 19953 volte maggiore a quella di riferimento; 57 dB a 501187 volte: numeri così grandi danno indicazioni sicuramente meno intuitive rispetto ai dB (almeno a coloro che ne hanno una certa abitudine).   ▲  

Conclusioni, e una "perla" letteraria

Nepero, il creatore della teoria dei logaritmi, aveva previsto correttamente che i suoi risultati avrebbero rivoluzionato il mondo scientifico dell'epoca. Pierre-Simon de Laplace (importantissimo matematico, fisico e astronomo francese, 1749-1827) scrisse che Nepero aveva "raddoppiato la vita degli astronomi": i logaritmi hanno semplificato moltissimo lo svolgimento dei calcoli, consentendo agli scienziati di perderci molto meno tempo. Non solo: questa nuova tecnica di calcolo ha anche favorito lo sviluppo dei commerci e delle attività imprenditoriali, in sostanza sulla nascita del mondo industriale a partire dalla seconda parte del XVII secolo.

Un'ultima curiosità: nel racconto "Avventure di tre russi e tre inglesi nell'Africa australe" di Jules Verne, c'è un personaggio, tale Nicolas Palander, che è talmente assorto nei suoi pensieri che non si accorge di essere circondato da una quantità di coccodrilli piuttosto affamati. I suoi compagni di avventure riescono in qualche modo a scacciarli sparando qualche fucilata. Al sentire gli spari, il Palander riconosce i suoi compagni e si mette a correre verso di loro, agitando il bloc notes che aveva in mano ed esclamando, come l'antico filosofo:

— Eureka! Ho trovato!
— Trovato cosa? — chiedono gli amici
— Un errore di decimale nel centotreesimo logaritmo nelle tabelle di James Wolston!

Verne ci spiega poi che con questa scoperta avrebbe incassato il premio di cento libbre messo in palio dall'editore di quelle tavole di logaritmi...

... peccato che di questo James Wolston io non sia riuscito a trovare traccia da nessuna parte. Certo è che Henry Briggs, il primo ad aver compilato tavole complete di logaritmi, aveva messo realmente in palio una somma da versare a chi avesse trovato errori nelle sue tavole: un ottimo sistema per farsele correggere da qualcun altro!   ▲  

Prossimo capitolo: il Regolo Calcolatore