Aritmetica: il Regolo Calcolatore

Sommario:

+ Contare
+ Sistemi di numerazione
+ Addizione e Sottrazione
+ Moltiplicazione
+ Divisione
+ Radice Quadrata
+ Elevamento a potenza
+ Logaritmi
– Il Regolo Calcolatore
      Uno strumento magico
      Le origini
      Doppia scala logaritmica
      il Regolo "moderno"
      Calcoli avanzati
      Qualche particolare curioso

Uno strumento magico

Ho sempre pensato che il regolo calcolatore fosse uno strumento di calcolo piuttosto limitato... fino a quando ho trovato nella biblioteca di mio padre questo libro del 1936 che ne rivela tutti i segreti:



Ci ho messo qualche giorno a capirli, ma ora posso dire... che era davvero uno strumento portentoso, in grado di fare calcoli di una complessità inaspettata.   ▲  

Le origini

Prima di iniziare a parlare del regolo calcolatore, riscrivo la definizione di logaritmo (di cui ho parlato nel capitolo precedente):

Il logaritmo decimale di un numero è l'esponente a cui elevare la base 10 per ottenere il numero dato.

Ecco come si esprime questo concetto in formule per due numeri N1 e N2, ma anche per il loro prodotto:



Fra le proprietà delle potenze (di cui invece ho parlato qui) c'è quella per cui il prodotto di due potenze di pari base è la stessa cosa di una potenza della stessa base con esponente uguale alla somma dei due esponenti di partenza. Quindi:



Dalle formule qui sopra risulta quindi che il logaritmo del prodotto è uguale alla somma dei logaritmi dei fattori. Il "trucco" alla base del funzionamento del regolo calcolatore è proprio il fatto che siamo riusciti a trasformare un prodotto in una somma!

A seguito degli studi di Nepero sui Logaritmi ci fu subito chi pensò di sfruttare l'idea in modo da velocizzare i calcoli, anche a scapito della precisione. Già nel 1623 Edmund Gunter, professore di astronomia al Gresham College di Londra, sviluppa una scala logaritmica sulla quale, con l'aiuto di un compasso, si possono eseguire graficamente moltiplicazioni e divisioni. Ecco... ma cos'è esattamente una scala logaritmica?



Si tratta di un righello in cui si riportano tacche a distanze proporzionali ai logaritmi dei numeri da 1 a 10. Nel diagramma sopra specifico che ogni tacca corrisponde al logaritmo del numero, ma la sigla "log" non è assolutamente necessaria:



Notare che a destra si scrive un 1 e non un 10: questa è una pratica utilizzata in tutti i regoli calcolatori. In pratica "si sa" che all'uno di destra corrisponde un 10; inoltre, come vedremo, in qualche caso l'uno di destra viene usato proprio come... 1 e non come 10!.

Ecco costruita la scala logaritmica! Ora ammettiamo di voler moltiplicare 1,5 per 4 con questa scala e un compasso, proprio come faceva il Gunter: basterà aprire il compasso a un'apertura corrispondente al logaritmo di 1,5 e riportare la stessa apertura sul 4. Vediamo il procedimento passo per passo:



La punta destra del compasso è posizionata sulla tacca del 1,5. La punta sinistra va messa sulla tacca del 1, perché ricordiamoci che quella tacca rappresenta il logaritmo di 1, e il logaritmo di 1 è 0. In questo modo l'apertura del compasso corrisponde alla differenza fra logaritmo di 1,5 e logaritmo di 1, quindi:

log( 1,5 ) – log( 1 ) = log( 1,5 ) – 0 = log( 1,5 )

Una volta trovata l'apertura del compasso, basta traslarlo verso destra:



Ecco che mettendo la punta sinistra del compasso sulla tacca del 4 mi ritrovo la punta destra sul 6 (ricordo che logaritmo di 1 fa 0):

log( 4 ) + [ log( 1,5 ) – log( 1 ) ] = log( 4 ) + log( 1,5 ) = log( 4 x 1,5 ) = log( 6 )

(infatti 1,5 x 4 = 6).

Con le stesse posizioni esatte avrei potuto fare il calcolo inverso: infatti con la stessa apertura corrispondente al numero 1,5, avrei potuto fare la divisione 6 : 1,5 = 4: considerando di mettere la punta destra del compasso sul 6, la punta sinistra mi avrebbe dato correttamente il quoziente cercato (alla differenza degli esponenti infatti corrisponde la divisione delle potenze).

log( 6 ) – [ log( 1,5 ) – log( 1 ) ] = log( 6 ) – log( 1,5 ) = log( 6 : 1,5 ) = log( 4 )   ▲  

Doppia scala logaritmica

Nel 1630 Edmund Wingate utilizza due scale di Gunter una di fronte all'altra per eseguire direttamente moltiplicazioni e divisioni, senza dover usare il compasso. Vediamo la moltiplicazione 1,5 x 3:



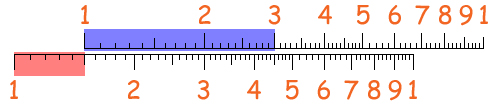
La zona rossa, nella scala inferiore, ha la stessa ampiezza del compasso che abbiamo visto sopra. Facendo partire l'origine (ossia la tacca del 1) della scala superiore proprio dalla fine della zona rossa, vedo che il limite destro della zona azzurra cade sul 4,5: infatti 1,5 x 3 = 4,5.

Questo procedimento va bene anche per calcolare numeri con ordini di grandezza diversi: es. 15 x 300 = 4500; in questi casi gli zeri in più o in meno, o gli eventuali spostamenti della virgola decimale, devono essere fatte "a mano" (in questo senso gli errori erano sempre in agguato... occorreva stare molto, molto attenti; l'ideale era capire più o meno qual era il risultato prima di calcolarlo, e cercare con il regolo solo la precisione delle cifre significative).

E se invece voglio calcolare 5 x 3? Qui nasce un problema, in quanto il tre sulla scala superiore si posiziona al di fuori della scala inferiore, quindi non riesco a leggere il risultato:



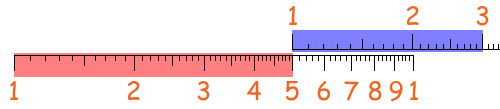
In questi casi si ricorre a un espediente: invece di moltiplicare per 3 si moltiplica per 0,3:



La zona marcata in azzurro qui sopra indica la differenza fra il logaritmo di 3 e il logaritmo di 10, quindi

log( 3 ) – log( 10 ) = log( 3 : 10 ) = log( 0,3 )

Allora basta posizionare, sul 5 della scala inferiore, non la tacca dell'uno sinistro della scala superiore, ma la tacca dell'uno destro:



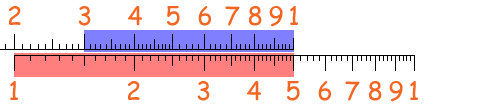
In questo modo la moltiplicazione 5 x 0,3 si riesce a fare senza uscire dalle scale, e il risultato si legge sul 1,5 della scala inferiore; ma siccome abbiamo moltiplicato per 0,3 e non per 3, occorre "aggiustare" il risultato moltiplicandolo per 10: il risultato finalmente è 15!

Dicevo che fra le proprietà delle potenze (e dei logaritmi) c'è quella per cui alla divisione delle potenze corrisponde la sottrazione degli esponenti. Quindi posso calcolare la divisione 6 : 4



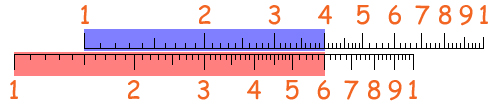
Dal grafico qui sopra si vede come sul 5 della scala inferiore non metto l'uno ma il 4 della scala superiore; l'uno della scala superiore si trova quindi sulla sinistra, e le aree rossa e azzurra si "sottraggono": ecco che la tacca 1 della scala superiore cade sul 1,5 della scala inferiore, determinando il risultato corretto.

Vediamo ora il calcolo "standard" (che in realtà ho scoperto essere tale solo leggendo il libro di cui ho parlato nella didascalia della foto): moltiplicazione e divisione in un colpo solo! In pratica è il calcolo di una proporzione: un numero moltiplicato per una frazione di cui sono dati numeratore e denominatore, come per esempio il calcolo dei tre mezzi di cinque (5 x 3 / 2).



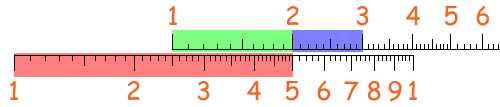
Allineando il 2 della scala superiore con il 5 della scala inferiore abbiamo che la tacca del 1 sinistro della scala superiore indica il quoziente 5 : 2 = 2,5. Le zone verde e azzurra insieme danno il fattore 3, quindi è come se si stesse moltiplicando per 3 il quoziente 5 : 2. Infatti il 3 sulla scala superiore cade proprio sul 7,5 di quella inferiore, che è il risultato esatto!

Ovviamente anche con le divisioni e con i calcoli misti (moltiplicazione e divisione insieme) può capitare di uscire "fuori scala"; ma c'è sempre il modo di sistemare le scale in modo da ottenere il risultato, come abbiamo visto per la moltiplicazione.   ▲  

Il Regolo "moderno"

Grazie a successivi miglioramenti, e al fatto che a partire dalla metà del XIX secolo l'industria meccanica di precisione ne ha permesso la costruzione in serie, il regolo calcolatore è diventato uno strumento di calcolo sostanzialmente standardizzato e di ampia diffusione. I regoli calcolatori sono costituiti dai seguenti elementi:

— un corpo su cui si trovano delle scale fisse
— un'asta scorrevole con delle scale mobili
— un cursore con una o più linee di riferimento



Le scale sono di vari tipi, indicate convenzionalmente da alcune lettere. Di scale semplici, come quelle del Wingate ce ne sono sempre due, una sull'asta scorrevole (scala C) e l'altra sul corpo (D). Altre scale servono per semplificare i calcoli quando si è in presenza di quadrati, cubi; radici quadrate e cubiche; funzioni trigonometriche... ecc.. Le scale di solito sono smistate fra il davanti e il dietro dell'asta e del corpo del regolo; in questo regolo sono presenti le scale:



K  — Scala dei cubi (corpo)
A  — Scala dei quadrati (corpo)
B  — Scala dei quadrati (asta)
ST— Seni e Tangenti per angoli piccoli (asta)
T  — Scala delle Tangenti per angoli > 6° (asta)
S  — Scala dei seni (e coseni) per angoli > 6° (asta)
C  — Scala dei numeri (asta)
D  — Scala dei numeri (corpo)
DI — Scala degli inversi dei numeri (1/x) (corpo)

Nel rovescio dell'asta, in alto, compaiono tre altre scale:

CI   — Scala dell'inverso dei numeri (1/X)
CF  — scala "ripiegata", che parte da pi-greco invece che da 1
CIF — scala dell'inverso, che parte da pi-greco

Per maggiore leggibilità delle foto che seguono, espongo i calcoli in modo che tutti i numeri stiano in un breve tratto del regolo, e senza fuoriuscire dalle scale; inoltre per brevità non spiego come si determinano gli zeri o la posizione della virgola: il mio scopo è solo mostrare di cosa erano capaci gli ingegneri quando usavano un regolo!   ▲  

Calcoli avanzati

Abbiamo visto che con due semplici scale si riesce a fare un'operazione mista di moltiplicazione-divisione in un colpo solo. E se invece volessi fare una divisione-divisione? Per fare questo bisogna ricondurre l'operazione che vogliamo fare a quella "standard" di moltiplicazione-divisione usando la scala dei reciproci; con questa scala si converte la divisione per B in una moltiplicazione per 1 / B:



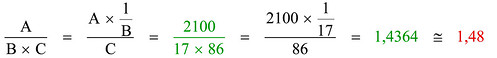
In verde indico i numeri di partenza e il risultato reale (calcolato con la calcolatrice); in rosso il risultato ottenuto con il regolo. Nel fare il calcolo tutti gli operandi devono essere ricondotti a numeri compresi fra 1 e 10, quindi 2100 diventa 2,1; 17 diventa 1,7 e 86 diventa 8,6. Vediamo allora come si usano le scale del regolo:



Si parte sovrapponendo il valore C (17) della scala C al valore A (2100) della scala D; come abbiamo già visto, la tacca 1 di sinistra dell'asta cade sul quoziente A/C. Portare il cursore sul valore B (86) della scala CI significa moltiplicare questo quoziente per l'inverso di B, quindi dividere tale quoziente ancora per B. La lettura del cursore sulla scala D fornisce il risultato cercato.

Ora vediamo una variante del calcolo precedente: una moltiplicazione-moltiplicazione. Anche in questo caso bisogna ricondurre l'operazione desiderata al caso standard, quindi si procede moltiplicando due fattori e dividendo per il reciproco del terzo, come indicato nelle formule:





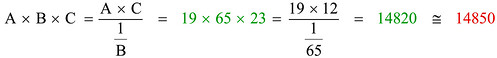
Sovrapporre il valore B (65) della scala CI al valore A (19) della scala D significa dividere A per il reciproco di B: per fare questo allineamento si usa il cursore, perché le scale CI e D non sono adiacenti. A questo punto leggere sulla scala D il numero corrispondente al valore C (12) della scala C significa moltiplicare ancora per C: ecco trovato il risultato desiderato!

Altro tipo di calcolo: una semplice divisione, ma il numeratore è una radice quadrata.





Si sposta il cursore sul valore A (350) della scala A dei quadrati (a questa posizione corrisponde, sulla scala D normale, il valore 18,7 che è proprio la radice quadrata di 350). Se ora faccio coincidere il valore B (1,51) della scala C sulla linea del cursore, avrò che il valore della scala D in corrispondenza del 1 sinistro dell'asta corrisponde alla divisione della radice quadrata di A per B, che è il risultato cercato.

Infine un calcolo davvero complesso, che richiede l'uso di ben quattro scale diverse. Si tratta del rapporto fra una radice cubica e una radice quadrata, il tutto moltiplicato per un numero normale. Per realizzare questo calcolo occorre montare l'asta del regolo al contrario, in modo da disporre sull'asta della scala dei quadrati (la scala B) .





Si porta il cursore sul valore A (7400) della scala K dei cubi (a questa posizione corrisponde, sulla scala D normale, il valore 19,487 che è proprio la radice cubica di 7400). Si sposta poi l'asta in modo da allineare al cursore il valore B (290) della scala B. A questo punto il valore della scala D in corrispondenza del 1 sinistro dell'asta corrisponde alla divisione della radice cubica di A per la radice quadrata di B; se invece cerco il valore C (1,3) sulla scala C, il valore corrispondente sulla scala D sarà il prodotto del quoziente precedente per C, che è il valore cercato.   ▲  

Qualche particolare curioso

Esistono infinite varianti di questi tipi di calcolo, che possono coinvolgere funzioni trigonometriche, logaritmiche, esponenziali... ora capisco come facessero gli ingegneri a progettare ciò che sono stati in grado di costruire negli ultimi due secoli, prima dell'avvento dell'elettronica (almeno fino ai primi anni '70 del secolo scorso).

Fra XIX e XX secolo sono stati costruiti anche regoli calcolatori di dimensioni imponenti: avevano scale di due metri di lunghezza, e un microscopio montato sul cursore. Con questi strumenti monumentali si riuscivano ad apprezzare fino a 6 cifre significative, sia negli operandi che nei risultati!

Ultima nota interessante: quando gli astronauti sono scesi sulla Luna (1969), le calcolatrici elettroniche ancora non erano state inventate, infatti la prima calcolatrice scientifica (la HP35) è solo del 1972. Allora gli astronauti sono andati sulla Luna... portandosi dietro un regolo calcolatore! La casa costruttrice di questi regoli "extraterrestri" infatti scrive sulle confezioni dei propri regoli: "5 moon flights", cinque voli sulla Luna!   ▲