Sommario:
– Elementi di Euclide: Riga e Compasso
Il Punto e la Retta
Il Cerchio
Riga e Compasso
Applicazione di una distanza?
Libro I, Proposizione 1
Libro I, Proposizioni 2 e 3
Scorciatoia!
+ Euclide vs. Hilbert: Punti, Linee e Superfici
+ Euclide: il Quinto Postulato
+ Elementi di Euclide: Costruzioni elementari
Gli Elementi
Il merito principale di Euclide (vissuto intorno al 300 a.C.) è stato di codificare in modo organico tutte le conoscenze di geometria (piana e solida), aritmetica (numeri razionali e irrazionali) e altre belle cose note nel mondo antico... insomma ha compilato l'enciclopedia di tutte conoscenze matematiche della sua epoca: stiamo parlando proprio dei suoi "Elementi". Qui ogni argomento è trattato a partire da un certo numero di definizioni e di postulati, per poi proseguire con la dimostrazione di un incredibile numero di teoremi assolutamente validi anche ai giorni nostri (la sua dimostrazione del teorema di Pitagora è di un'eleganza squisita).
I paragrafi che seguono non vogliono essere esaustivi dell'argomento, ma dare qualche spunto che possa incuriosire e possibilmente far apprezzare la grandezza dell'opera di Euclide. ▲
Il Punto e la retta
[d. 1] — Un punto è ciò che è privo di parti.Credo che sia la più celebre definizione della geometria: è la prima fra quelle elencate da Euclide nei Libro Primo suoi "Elementi". Le successive tre invece sono:
[d. 2] — Una linea è una lunghezza senza larghezza.(Se fossi uno che non ne sa niente, non so se da queste definizioni, soprattutto l'ultima, saprei immaginare cos’è una linea retta... meno male che tutti noi abbiamo almeno una volta tracciato una linea con righello e lapis!)
[d. 3] — Le estremità di una linea sono punti.
[d. 4] — La retta è quella linea che giace sui suoi punti in modo uniforme.
Ricapitolando: secondo queste definizioni, una linea non solo "non ha larghezza", ma è fatta da punti "che sono privi di parti". Questi punti sono quindi piccoli, piccolissimi, diciamo pure infinitesimali: se si potesse tracciare una linea ideale, essa risulterebbe assolutamente invisibile. Questo ci deve far riflettere sul livello di astrazione raggiunto dai geometri greci dell'antichità: le loro costruzioni sono solo ideali, in quanto le "figure" che possiamo realizzare con i mezzi grossolani di cui ci serviamo servono solo per rappresentare le cose in modo da rendercele più facilmente comprensibili.
Per quanto riguarda la retta, Euclide stabilisce anche due "postulati", ovvero enunciati che, pur non essendo dimostrati, sono considerati veri:
[p. 1] — Tra due punti qualsiasi è possibile tracciare uno ed un solo segmento.
[p. 2] — Si può prolungare un segmento oltre i due punti indefinitamente. ▲
Il Cerchio
Definizioni (Libro I):
[d. 15] — Dicesi cerchio una figura piana delimitata da un'unica linea tale che tutti i segmenti che terminano su di essa a partire da un medesimo punto fra quelli interni alla figura, siano uguali fra loro.Postulato:
[d. 16] — Quel punto si chiama centro del cerchio.
[p. 3] — Dato un punto e una lunghezza, è possibile descrivere un cerchio. ▲
Riga e Compasso
Andiamo a scuola ci diventano subito familiari gli strumenti chiamati Riga e Compasso, che effettivamente servono per tracciare le Rette e i Cerchi definiti da Euclide. Infatti, dati due punti qualsiasi, essi possono essere congiunti con un segmento rettilineo; e si può anche proseguire il disegno prolungando a piacimento il segmento oltre i punti dati:

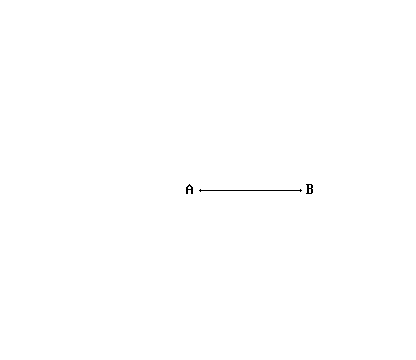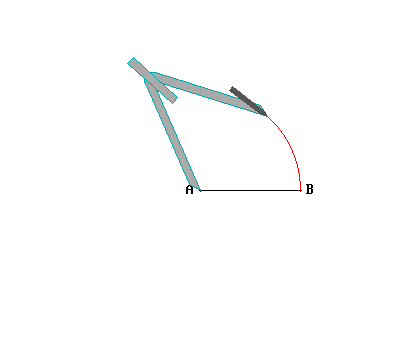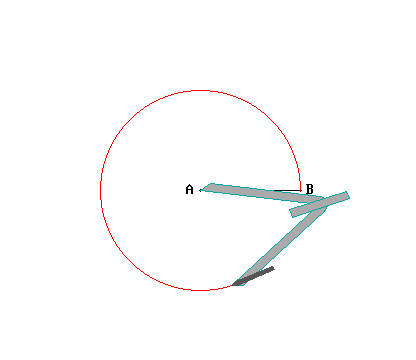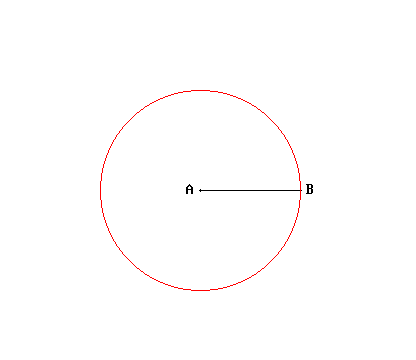
Per quanto riguarda il cerchio, dato un centro e uno dei punti sulla sua circonferenza, con un compasso è possibile tracciare tutti gli altri punti alla stessa distanza dal centro:
Ecco, per quanto Euclide non li nomini mai, Riga e Compasso sono i due soli strumenti ammessi nelle sue costruzioni geometriche. Detto altrimenti, sono gli strumenti soli e sufficienti che consentono la rappresentazione grafica di tutte le sue dimostrazioni! ▲
Applicazione di una distanza?
nelle costruzioni geometriche capita di dover riportare (o, più esattamente, "applicare") la lunghezza di un segmento a un altro segmento. E qui viene fuori un problema non da poco, in quanto la riga di Euclide NON è graduata. "Misurare" un segmento con un righello e poi riportare quella misura da un’altra parte non è certo un sistema esatto, e infatti non viene mai preso in considerazione da Euclide.
L'unica altra possibilità dunque è quella di utilizzare il compasso. Visto che, come abbiamo visto, il compasso è in grado di determinare tutti i punti equidistanti da un punto dato (centro), non è che lo si potrebbe usare anche per applicare una lunghezza, come mostrato qui sotto?
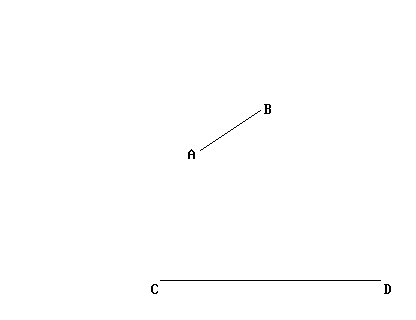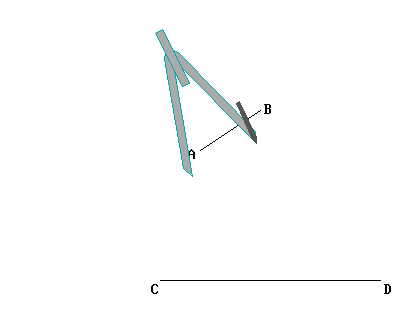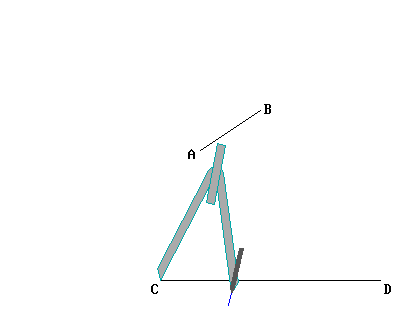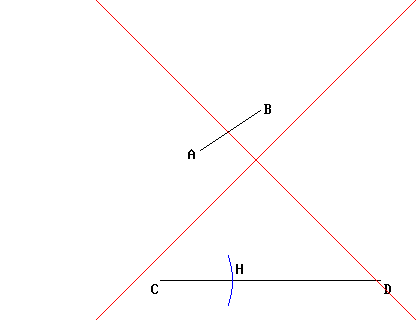
La risposta è... Nì. Nel senso che questa è una pratica usata continuamente, ma non è giustificata direttamente dai postulati di Euclide; quindi in teoria è un’operazione vietata. Dobbiamo immaginare che il compasso di Euclide abbia la particolarità di richiudersi automaticamente appena viene allontanato dal foglio: proprio come nell’animazione più sopra, quella dove viene mostrato il disegno della circonferenza.
Ora è ovvio che Euclide non si poteva arenare di fronte a questa difficoltà, infatti dedica le prime tre proposizioni del Libro Primo dei suoi Elementi proprio al superamento di quest’ostacolo. ▲
Libro I, Proposizione 1
Nella prima proposizione mostra come si costruisce un triangolo equilatero su un segmento dato (equilatero è quel triangolo che ha i tre lati uguali):
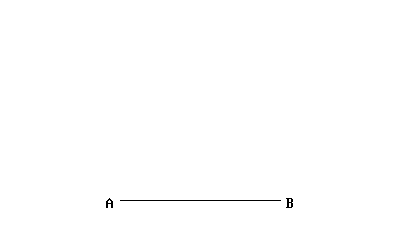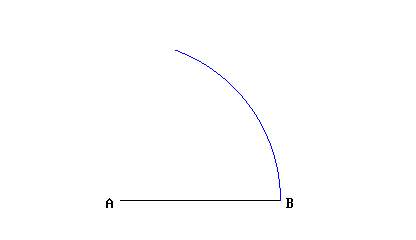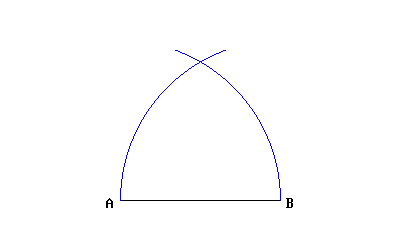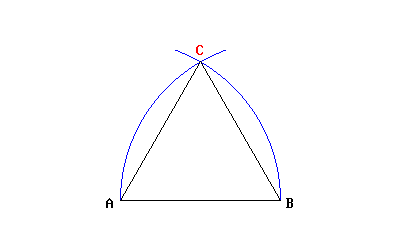
Come si vede dall’animazione, vengono tracciati due archi di cerchio, entrambi di raggio pari al segmento dato; ogni volta il compasso viene richiuso e riaperto: ecco che NON stiamo commettendo l’infrazione di tenere il compasso aperto fra il disegno di un arco e l’altro. Non credo che sia necessario dimostrare che le distanze AB, AC e BC sono uguali: per completare il triangolo a questo punto è sufficiente tracciare i due lati mancanti. ▲
Libro I, Proposizioni 2 e 3
Nelle proposizioni 2 e 3 del Libro Primo, che qui vengono unite insieme in un’unica animazione, Euclide riesce a trasportare (o, più precisamente, applicare) il segmento AB sul segmento CD:
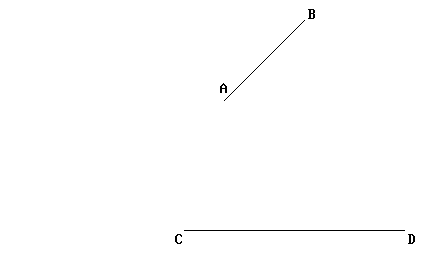
Ecco il procedimento (più in basso l'animazione completa):
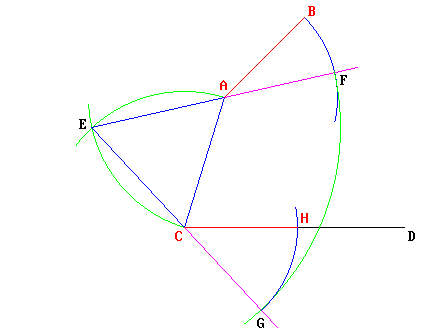
— Si traccia un segmento fra i punti A e C, e su questo segmento si costruisce il triangolo equilatero ACE; i lati AC e AE vengono prolungati adeguatamente (disegnati in viola).
— Puntando il compasso in A si riporta la lunghezza di AB in modo da determinare il punto F; il segmento EF è quindi la somma dei due segmenti EA (lato del triangolo) e AF = AB.
— Puntando il compasso in E, si riporta la lunghezza EF in modo da determinare il punto G, per cui EF = EG. Ma siccome EA = EC (lati dello stesso triangolo equilatero), CG non può che essere uguale a AF = AB.
— Puntando il compasso in C posso finalmente riportare la lunghezza CG sul segmento CD: ecco che quindi CH = AB.
Come promesso, qui sotto mostro la costruzione completa:
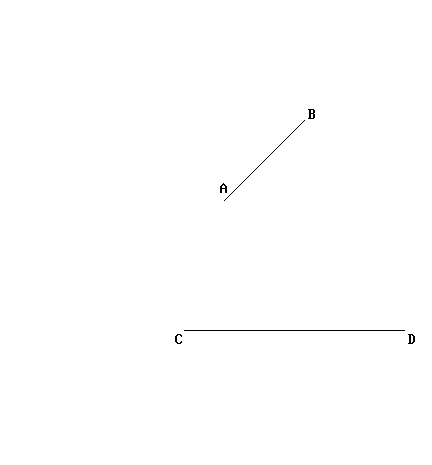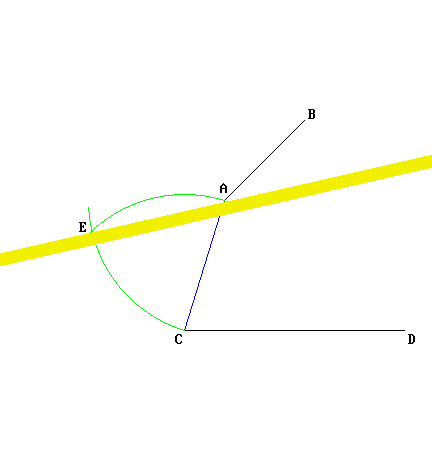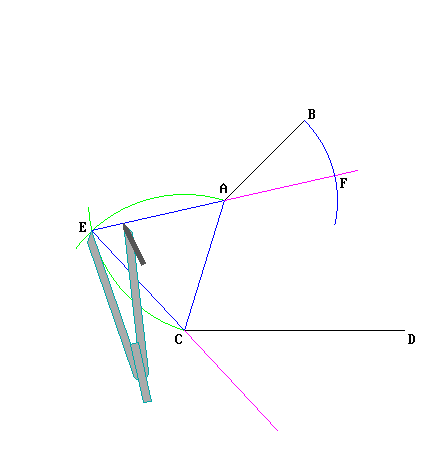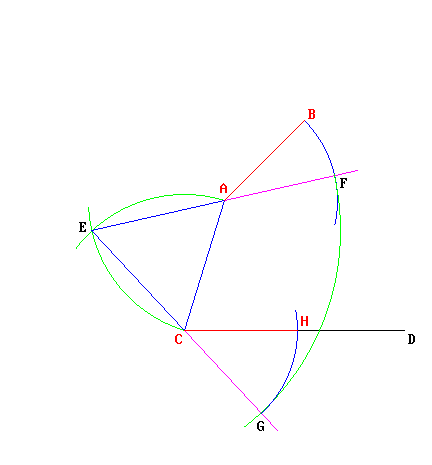
Ecco dimostrato come una lunghezza può essere trasportata in modo esatto, da un punto a un altro del foglio, senza trasgredire alle "regole" di Euclide. Il fatto che questa operazione sia fattibile basandosi su definizioni e postulati già presenti è il motivo per cui Euclide non ha avuto bisogno di aggiungere, fra i suoi postulati, qualcosa che affermasse la possibilità di trasportare una lunghezza. ▲
Scorciatoia!
Per nostra fortuna possiamo usare il procedimento che avevo dichiarato "vietato" (vedi sopra): possiamo liberamente usare quella scorciatoia per semplificarci il lavoro, ma solo dopo aver dimostrato la fattibilità di questa operazione con i metodi "prescritti".
I quali metodi prescritti sono: usare righe non graduate e compassi che si richiudono non appena allontanati dal foglio. Con l'aiuto di questi due soli strumenti Euclide è riuscito a costruire un castello incredibile... che inizieremo ad "esplorare", un po' per volta, a partire dal prossimo capitolo. ▲
Forse lei insegna? Se può essere utile, suggerisco http://descrittiva.blogspot.com/. Grazie, comunque, per i ricchi spunti in ambiti che non mi sono familiari.
RispondiEliminaSalve. Sono arrivato al suo blog dopo aver visto le sue stupende costruzioni geometriche (soprattutto sui poligoni regolari) su Flickr, ma ho visto che sono presenti anche su Wikipedia. Sto provando a fare le stesse costruzioni con Geogebra ed i suoi lavori sono stati per me molto utili.
RispondiEliminaVolevo chiederle se è possibile sapere quale software ha usato per le sue animazioni delle costruzioni geometriche (gif con matita riga e compasso).
La ringrazio sin d'ora.
Un saluto
Marco