Pillole di Scienza: newton

Visualizzazione post con etichetta newton. Mostra tutti i post

Ottica: l'arcobaleno

Sommario:

+ Introduzione
+ Riflessione
+ Rifrazione
+ Diffrazione
+ Cannocchiale e Aberrazione sferica
+ Dispersione e Telesopio di Newton
+ Etere Luminifero
+ Birifrangenza e Polarizzazione
+ Interferenza
– Arcobaleno
      Riflessione e Rifrazione
      Leggi di Fresnel
      Una goccia d'acqua
      Molte gocce d'acqua
      Due arcobaleni

Riflessione e Rifrazione

Nel corso dei capitoli precedenti abbiamo visto come, già nel XVII secolo, fossero stati compresi i fenomeni di Riflessione e Rifrazione. Tale comprensione però si limitava alle "leggi degli angoli", ovvero la relazione fra gli angoli di incidenza e di riflessione / rifrazione della luce quando un raggio attraversa la superficie di separazione fra due materiali diversi (es. aria / acqua o aria / vetro).

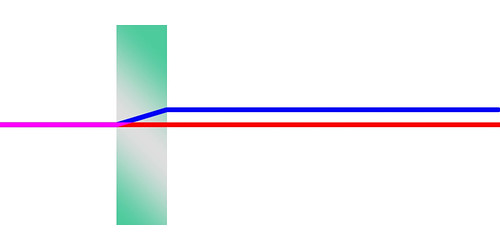
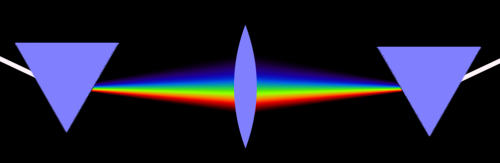
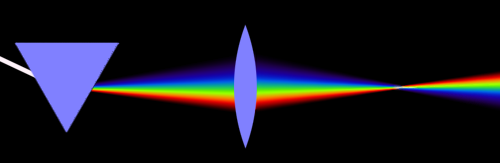
I due fenomeni coesistono quasi sempre: il caso classico è una lastra di vetro attraverso la quale la luce passa (rifrazione), ma dalla quale viene anche riflessa. Non solo: questi fenomeni avvengono molteplici volte in corrispondenza di entrambe le superfici della lastra di vetro:

Un raggio di luce, proveniente dall'angolo in alto a sinistra, raggiunge la lastra di vetro nel punto 1. Una certa quantità di luce viene riflessa (raggio rosso), il rimanente entra nel vetro secondo il dovuto angolo di rifrazione (raggio blu). Quando questo raggio di luce raggiunge la faccia opposta della lastra di vetro, nel punto 2, avviene il fenomeno complementare: una quota di luce viene rifratta all'esterno (raggio rosso), mentre il rimanente viene riflesso nuovamente all'interno della lastra di vetro. Quest'ultimo meccanismo viene poi ripetuto nei punti 3, 4, 5... in teoria, all'infinito. ▲

Leggi di Fresnel

Se si volesse fare il calcolo esatto di quanta luce totale attraversa il vetro, e quanta ne viene riflessa, non sarebbe sufficiente conoscere le leggi degli angoli come la legge di Snell, ma occorrerebbero anche leggi quantitative: sono proprio le Leggi di Fresnel.

Le quali leggi di Fresnel tengono conto dell'angolo di incidenza della luce, dei coefficienti di rifrazione dei materiali interessati, e anche della Polarizzazione della luce: infatti si usa il plurale, "le" leggi di Fresnel, che sono due da utilizzare a seconda dei piani di polarizzazione della luce incidente. E siccome le complicazioni non non finiscono mai, bisogna tenere conto anche della variazione dei coefficienti di rifrazione a seconda del colore della luce: si tratta del fenomeno di Dispersione, scoperto da Newton.

Ora che è stato fatto l'elenco dei fenomeni che intervengono nella produzione dell'arcobaleno, possiamo cominciare a spiegarne il funzionamento. Anche se i programmi che ho scritto per creare le immagini che seguono tengono conto nel modo più accurato possibile di tutti gli aspetti della faccenda, la spiegazione sarà molto elementare; chi fosse interessato ai dettagli matematici delle leggi coinvolte... potrà trovare moltissimo materiale sul web, che d'altra parte ho spesso consultato anch'io! ▲

Una goccia d'acqua

Per ottenere un arcobaleno sono necessarie la luce solare e qualche goccia d'acqua. Vediamo allora cosa succede di un singolo raggio di luce che incide su una singola goccia d'acqua (la cosa non è molto diversa a quanto già descritto riguardo la lastra di vetro). Nota: per adesso vedremo i fenomeni "di profilo", cioè avendo il sole alla nostra sinistra invece che alle nostre spalle: solo in questo modo si possono vedere le traiettorie percorse dai raggi luce in arrivo dal sole, e le loro successive riflessioni / rifrazioni.

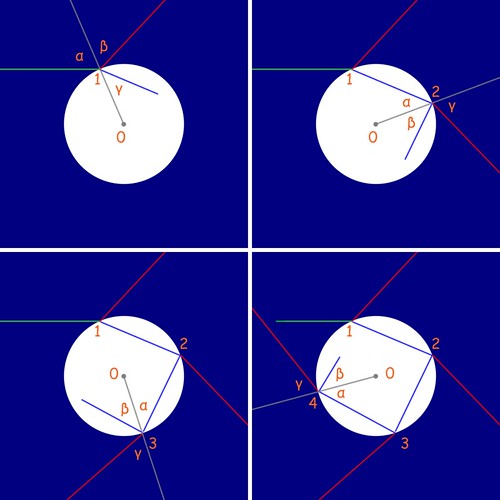
1 — La luce proveniente da sinistra (raggio verde, nella figura in alto a sinistra) colpisce la goccia nel punto 1. Una certa quantità di luce viene riflessa secondo l'angolo β (linea rossa), mentre la luce rimanente viene rifratta all'interno della goccia secondo l'angolo γ (linea blu).

2 — La luce rifratta nel punto 1 prosegue la sua corsa e incontra nuovamente la superficie della goccia nel punto 2 (in alto a destra): qui avviene il fenomeno complementare a quello descritto nel punto 1, infatti una quota parte viene rifratta all'esterno della goccia (linea rossa) mentre il rimanente viene ancora riflesso e permane all'interno della goccia (linea blu).

3, 4 — In basso a sinistra e destra vediamo il ripetersi del fenomeno descritto al punto 2. In realtà il meccanismo si ripete ancora molte volte: fino a quando cioè all'interno della goccia il raggio di luce continua ad essere riflesso, con intensità sempre minore... in teoria un numero infinito di volte!

Per adesso, nello studio dell'arcobaleno ci limiteremo ad analizzare questi quattro raggi di luce uscenti dalla goccia: come già detto ce ne sono anche altri, ma contribuiscono in modo marginale al fenomeno che stiamo studiando (ne parleremo alla fine).

Nell'animazione che segue, per ogni raggio di luce che arriva sulla goccia (linee in bianco, da sinistra) escono quattro raggi rossi, frutto dei vari fenomeni di riflessione / rifrazione già descritti:

La cosa appare molto caotica: questo dipende dal fatto che per adesso non si è tenuto conto dell'intensità dei vari raggi, ma solo dei loro angoli. Vediamo adesso succede tenendo conto anche di questo aspetto:

Nell'immagine sopra si vede l'intensità della luce prodotta separatamente da ciascuno dei quattro tipi di raggio di luce che esce dalla goccia d'acqua: in alto a sinistra la prima riflessione, in alto a destra e poi in basso i tre fenomeni di riflessione / rifrazione a cui sono soggetti i raggi di luce via via che "rimbalzano" sulla superficie interna della goccia.

Le intensità di questi quattro fasci di luce sono molto diverse l'una dall'altra. Il fascio più luminoso è il secondo, infatti la percentuale di luce che entra nella goccia per uscirne immediatamente è di gran lunga superiore alla quantità di luce che segue gli altri percorsi (così come, in una finestra, la luce che la attraversa è in quantità nettamente superiore alla luce che ne viene riflessa).

Come fare allora per vedere il sovrapporsi di tutti i fenomeni, senza rimanere "abbagliati" da quello più intenso? Basta ignorare proprio quest'ultimo! Infatti vediamo cosa succede di questo fascio di luce se ci si allontana dalla goccia:

Per quanto focalizzandosi in un punto vicino alla goccia si abbia un picco di luminosità molto elevato, allontanandosene la luce si disperde molto velocemente; e, vista da grande distanza che ci sarà fra l'osservatore e le gocce che danno luogo all'arcobaleno, l'effetto causato da questo fascio di luce diventa assolutamente trascurabile.

Nell'immagine che segue si vede la composizione dei fasci di luce nelle loro reali intensità reciproche, avendo omesso solo il fascio di cui sopra:

Verso destra si intravedono, debolissimi, i doppi fasci di luce derivanti dalla riflessione della luce quando incontra la goccia per la prima volta: anche questo fenomeno potrà essere trascurato. Ciò che è interessante piuttosto sono le linee nitide, frutto della terza e della quarta rifrazione: saranno proprio queste linee a dar luogo ai due arcobaleni, quello primario e quello secondario.

Fino ad ora abbiamo visto cosa succede usando solo luce rossa: vediamo adesso cosa succede sovrapponendo l'effetto generato da fasci di luce di tutti i colori:

Alle estremità delle linee più luminose, a sinistra, si intravedono delle frange colorate: queste sono dovute al diverso coefficiente di rifrazione associato a ciascun colore della luce, per cui le relative linee di maggiore intensità vengono emesse con angoli leggermente diversi l'uno dall'altro.

Allontaniamoci un po' dalla goccia:

I due fasci di luce si incrociano, e le frange sono sempre più colorate. Allontaniamoci ancora:

Ora che abbiamo portato la goccia fuori dallo schermo, non si vedono più i picchi ad alta luminosità intorno alla goccia stessa, che costringevano a tenere bassa la luminosità dell'immagine; adesso con una luminosità ottimale, si vedono bene i due fasci di luce, colorati come se fossero passati attraverso un prisma, anche se l'arcobaleno risulta da una combinazione molto più complicata di fattori. ▲

Molte gocce d'acqua

Insomma, abbiamo visto "cosa esce" da una goccia d'acqua illuminata dal sole. Ma cosa vede esattamente un osservatore che la guardi da lontano?

Dipende. Nel senso che dipende dalla posizione reciproca fra goccia e occhio. Se l'osservatore si trova nella posizione 1, il suo occhio viene illuminato dalla sola luce rossa dell'arco primario; se in posizione 2 o 3, il verde o il viola dello stesso arco.

Se l'osservatore si trova nella posizione 4 o 5, vede il rosso dell'arco secondario, quello dovuto alla quarta riflessione / rifrazione del raggio di luce all'interno della goccia. L'arcobaleno secondario ha le seguenti caratteristiche:

— Ha i colori disposti in ordine inverso (questo è dovuto al fatto che i raggi di luce subiscono una riflessione in più rispetto all'arcobaleno primario);
— È più ampio (la riflessione aggiuntiva causa un'amplificazione delle differenze negli angoli);
— Ha intensità minore (a ogni riflessione / rifrazione segue una diminuzione dell'intensità del raggio luminoso).

Nell'immagine sopra ho indicato anche la posizione 6: questa indica una fascia scura, chiamata "Banda di Alessandro". Infatti mentre all'esterno della zona compresa fra i due fasci di luce si ha un bagliore diffuso, la zona interna non viene raggiunta da nessun raggio di luce uscente dalla goccia (a parte quello che deriva dalla prima riflessione della luce solare, ma che, debole in partenza,con la distanza si disperde molto velocemente fino a diventare assolutamente trascurabile). L'Alessandro che dà il nome alla banda scura è Alessandro d'Afrodisia, filosofo greco del III secolo d.C., che è stato il primo a descrivere questo fenomeno.

Nell'immagine sopra abbiamo capito cosa vedrebbe un osservatore spostandosi all'interno dei fasci di luce emessi da una singola goccia. Naturalmente ciò che accade realmente è il fenomeno inverso: l'osservatore sta fermo, e viene investito dai fasci di luce che lo raggiungono da una miriade di gocce diverse.

Nell'immagine sopra a sinistra il punto di vista, indicato dall'occhio, viene investito dalla luce rossa dell'arco primario, quindi l'osservatore ha l'impressione che quella goccia "sia" proprio di colore rosso. Nell'immagine di destra invece l'occhio viene investito dalla luce verde dell'arco secondario: ecco che quest'altra goccia appare di colore verde.

L'arcobaleno è creato da una miriade di gocce disposte in posizioni diverse l'una dall'altra. Ecco cosa vede l'osservatore (nell'immagine che segue l'arcobaleno è visto "di profilo"):

Si vede bene come tutte le gocce "colorate" di rosso nell'arco primario sono perfettamente allineate rispetto all'osservatore, così come sono allineate le gocce di tutti gli altri colori: questo accade perché i raggi solari sono tutti paralleli fra loro, e gli aspetti geometrici delle riflessioni / rifrazioni sono identici per ciascuna goccia. Allora, la condizione affinché le gocce si mostrino tutte di un determinato colore (in questo caso il rosso), l'unica condizione necessaria è che l'angolo α compreso fra la direzione di arrivo della luce solare (le linee bianche, da sinistra) e la linea che congiunge la goccia all'osservatore, deve essere costante: per quanto riguarda la luce rossa dell'arco primario, l'angolo è di circa 42 gradi e mezzo. ▲

Due arcobaleni

Come dicevo, le immagini sopra mostrano il funzionamento dell'arcobaleno con una vista di profilo, infatti non c'è ancora niente che assomigli a un arco! Lo schema che segue invece mostra il fenomeno in prospettiva:

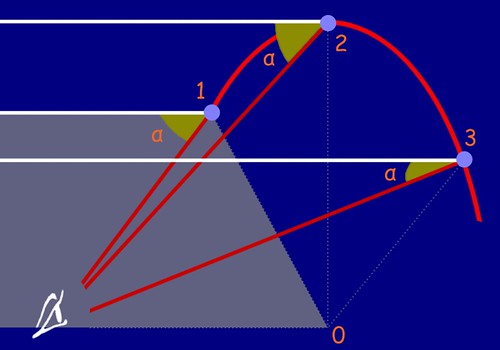
Per ogni goccia bisogna prendere in considerazione il piano che giace sulla linea percorsa dalla luce solare che la illumina, e che passa dall'occhio dell'osservatore (l'area indicata in grigio indica il piano relativo alla goccia 1). Se l'angolo α compreso fra la linea di luce incidente (indicata in bianco) e la linea che congiunge la goccia con l'osservatore è proprio di 42,5° allora l'osservatore vedrà quella goccia illuminata di rosso; altrimenti l'osservatore vedrà il colore associato a un angolo diverso... oppure nessun colore.

Vediamo la cosa da un altro punto di vista: l'area di cielo che si colorerà di rosso sarà il "luogo" delle gocce che stanno al vertice di un angolo di 42,5°, misurato fra la linea di luce che illumina la goccia e la congiungente fra goccia e osservatore. Questo luogo non può che essere circolare: è come se usassimo un compasso con apertura costante (ecco quindi spiegata la forma di arco circolare dell'arcobaleno).

Il discorso ovviamente vale per qualsiasi altro colore / angolo: angoli più piccoli danno luogo ad archi concentrici di raggio minore. Gli angoli più grandi, relativi all'arcobaleno secondario, danno luogo agli archi di raggio maggiore relativi proprio a questo secondo arcobaleno; gli angoli intermedi provocano la fascia più scura compresa fra i due: la Banda di Alessandro.

Per finire, vediamo finalmente un arcobaleno visto frontalmente. Nell'immagine che segue (la stessa che c'è in apertura) ho sovrapposto una foto presa dal web di un arcobaleno doppio all'immagine ottenuta al computer. Il programma calcola la somma dei contributi di luce che raggiungono l'osservatore per ogni colore (al quale corrisponde un diverso indice di rifrazione, e una diversa composizione RGB, rosso-verde-blu) per ogni goccia, tenendo conto anche della polarizzazione della luce a ogni evento. Direi che la somiglianza è davvero notevole... ▲

Ulteriore arcobaleno

Per finire, manca un accenno alla questione lasciata in sospeso: cosa succede delle ulteriori riflessioni / rifrazioni all'interno di ciascuna goccia?

Ecco qui i raggi generati dalle due successive rifrazioni: hanno le stesse caratteristiche di quelli già descritti e sono anch'essi in grado di generare un arcobaleno. Hanno però intensità molto più debole dei primi due, e di fatto solo in condizioni atmosferiche eccezionali si riesce ad apprezzare il più intenso dei due. Il quale, a differenza dei primi due, non va però cercato dando le spalle al sole: questo effimero arcobaleno viene a trovarsi in controluce, ecco anche spiegato perché è così difficile da osservare. ▲

Ottica: Birifrangenza e Polarizzazione

Sommario:

+ Introduzione
+ Riflessione
+ Rifrazione
+ Diffrazione
+ Cannocchiale e Aberrazione sferica
+ Dispersione e Telesopio di Newton
+ Etere Luminifero
– Birifrangenza e Polarizzazione
      Lo Spato d'Islanda
      Newton e Huygens
      La Polarizzazione della Luce
      Onde Longitudinali e Trasversali
      Étienne-Louis Malus
      Esperimenti fatti in casa
+ Interferenza
+ L'arcobaleno

Lo Spato d'Islanda

Nei capitoli precedenti abbiamo lasciato Newton e Huygens a becchettarsi sulle diverse interpretazioni dei raggi di luce. Erano corpuscoli, come sosteneva Newton, oppure onde, secondo il pensiero di Huygens?

Anno 1669: colpo di scena. Il medico danese Rasmus Bartholin (1625-1698) osserva uno strano minerale: un tipo di calcite, chiamato anche Spato Vetrino, o Spato d'Islanda (quello della foto in alto). Bartholin nota che gli oggetti osservati attraverso questo materiale appaiono sdoppiati, come se questa calcite fosse capace di esibire contemporaneamente due indici di rifrazione diversi; da qui il nome di questo strano fenomeno:

In questa foto il cristallo è appoggiato su un foglio bianco che porta stampata la parola CALCITE con caratteri semplici; il fatto che la scritta risulti doppia, sfalsata in verticale, è conseguenza di un comportamento davvero eccezionale di questo materiale (e pochi altri) assolutamente naturale: la birifrangenza.

Vediamo cosa succede a un raggio di luce (indicato in viola, proveniente da sinistra) che attraversa un cristallo di Spato d'Islanda, perfettamente lucidato e con le facce parallele fra loro.

Secondo la legge di rifrazione, un raggio di luce che arrivi sul cristallo in direzione perfettamente perpendicolare alla sua superficie non deve deviare, né la cosa deve accadere all'uscita del cristallo stesso: nell'immagine qui sopra tale raggio è indicato in rosso, e viene chiamato "raggio ordinario". Il cristallo però esibisce un fenomeno aggiuntivo: all'interno del cristallo, una parte della luce (il cosiddetto "raggio straordinario") segue un percorso diverso, in modo da fuoriuscire da un punto diverso. All'uscita dal cristallo i due raggi proseguono paralleli fra loro... ma cosa mai può essere accaduto all'interno del cristallo affinché il raggio in entrata si sia diviso in due? ▲

Newton e Huygens

Immediatamente iniziano i tentavi di spiegare il fenomeno: per Newton la causa sta nei suoi corpuscoli, che potrebbero avere qualche asimmetria nella loro struttura. Huygens dal canto suo è convinto di riuscire a spiegare il fenomeno grazie alle sue onde longitudinali, ma un bel giorno...

... proprio Huygens esegue un esperimento che lo farà capitolare. Egli prende due cristalli e li allinea in modo che ciascuno di essi faccia deviare il raggio straordinario esattamente nella stessa direzione. Poi fa passare un raggio di luce attraverso i due cristalli... cosa succederà adesso?

Huygens è convinto che ciascuno dei due raggi uscenti dal primo cristallo abbia la stessa natura del raggio di luce entrante, ovvero un fascio di onde longitudinali. Si aspetta quindi che nel passare dal secondo cristallo i due raggi diventino quattro, o qualcosa del genere... ma siccome il risultato dell'esperimento è confuso, per capire meglio cosa sta succedendo oscura uno dei raggi per volta.

Con grande sorpresa Huygens vede che, come mostrato in figura, il raggio straordinario non si divide assolutamente ma subisce una seconda rifrazione straordinaria; se invece lascia transitare soltanto il raggio ordinario, questo prosegue in linea retta (secondo la normale legge di rifrazione) attraverso entrambi i cristalli.

Lo stupore di Huygens deriva dal fatto che le onde evidentemente "conservano" memoria del percorso già compiuto; insomma hanno un qualche attributo che consente loro di comportarsi in modi diversi nel caso che abbiano già attraversato un cristallo oppure non lo abbiano ancora fatto... e questo attributo le onde longitudinali non ce l'hanno proprio. Newton dirà infatti che la luce "ha lati"... cosa che però non costituisce una spiegazione compiuta dei fenomeni, infatti neanche Newton ha idee molto chiare in proposito.

Ricordo che in questo primo esperimento Huygens ha orientato i cristalli nella stessa direzione "ottica". Ruotando i cristalli l'uno rispetto all'altro, egli ottiene una casistica assai complessa di risultati per cui a un certo punto dichiarerà

di non essere in grado di individuarne le cause. Ma per questa ragione di non desistere dal descriverli con lo scopo di dare ad altri l'opportunità di indagarli.

Per andare avanti nella comprensione di questi fenomeni si dovrà aspettare più di un secolo; in questo lasso di tempo la scena sarà dominata dalle teorie corpuscolari di Newton (più per l'importanza del personaggio che per ragioni scientifiche) in quanto non era stata ancora trovata nessuna prova decisiva. ▲

La Polarizzazione della Luce

Nel 1808 viene fatta, in modo più o meno casuale, un'importante scoperta: l'ufficiale francese (ma anche ingegnere, fisico, e matematico, 1775-1812) Étienne-Louis Malus sta "giocando" con un cristallo di calcite, quando si accorge che uno dei raggi... è sparito! Girando il cristallo, vede attenuarsi questo raggio e "accendersi" l'altro finché il primo si spegne e il secondo raggiunge la massima intensità.

Lì per lì pensa a un cristallo "difettoso", ma poi gli viene il sospetto che il fenomeno possa dipendere dalla luce che lo attraversa: infatti non sta usando la luce del sole diretta, bensì un fascio di luce riflesso da una finestra. Allora ripete gli esperimenti con la luce solare diretta: il cristallo in questo caso funziona normalmente, con i due raggi sempre visibili, di cui quello straordinario che "ruota" normalmente assieme al cristallo.

Malus aveva scoperto un nuovo fenomeno: la polarizzazione della luce a causa della sua riflessione. Malus era un convinto sostenitore della teoria ondulatoria di Huygens. Nel fare i suoi esperimenti però accumula sempre più indizi che gli fanno pensare che non si tratti di onde longitudinali, come credeva Huygens, bensì trasversali. Ma cos'hanno mai di diverso questi due tipi di onde? ▲

Onde Longitudinali e Trasversali

Immaginiamo di far oscillare sul piano verticale una corda come quelle che usano i bambini per saltare. Se la corda passa attraverso due tavole di una staccionata, l'onda si propaga senza alcun problema:

mentre se la corda passa attraverso una fessura orizzontale, l'onda non riesce a superare l'ostacolo:

La corda che oscilla come mostrato in queste due animazioni si muove secondo un moto ondulatorio trasversale; nelle onde longitudinali invece questo fenomeno di "arresto" non si verifica:

Vediamo ora cosa succede se le onde non sono né orizzontali né verticali, ovvero se non sono né allineate né perpendicolari alla fessura che funge da ostacolo:

Ogni onda può sempre essere scomposta in due "proiezioni" ortogonali fra loro. Nel quadrante di sinistra si vede in viola l'orientamento del piano sul quale si propaga l'onda luminosa, e le proiezioni di questo sul piano orizzontale (blu) e verticale (rosso). Sulla destra si vede lo sviluppo dell'onda originale (viola) e le sue scomposizioni (rossa e blu); la somma di queste due onde dà come risultato esattamente l'onda originale, quindi le due rappresentazioni di questo raggio di luce sono assolutamente equivalenti. Nell'ultima sezione di destra si vede transitare solo la componente verticale dell'onda, come se in quel punto fosse stata applicata la "staccionata" verticale (ovvero un filtro polarizzatore adeguatamente orientato).

Ovviamente il Sole ci invia raggi luminosi, diciamo così, "alla rinfusa", cioè orientati secondo qualsiasi piano di oscillazione trasversale. Per semplificare i calcoli si scompone ogni raggio nelle sue componenti verticale e orizzontale:

a sinistra, in viola, si vede un certo numero di onde variamente orientate; nella parte centrale la loro scomposizione; a destra il risultato ottenuto totalizzando le componenti orizzontale e verticale delle onde incidenti. ▲

Étienne-Louis Malus

Torniamo adesso al lavoro di Malus. A seguito della sua scoperta inizia a studiare gli effetti di rifrazione e riflessione della luce polarizzata, ovvero di luce composta solo da onde che giacciono su un unico piano per volta. Le leggi di Snell che descrivono gli angoli di riflessione e rifrazione (ordinaria) rimangono sempre valide, indipendentemente dall'angolo di polarizzazione della luce incidente. Ciò che cambia sono le intensità: la luce che incide su un materiale trasparente viene in parte riflessa e in parte rifratta, ma queste proporzioni variano al variare della polarizzazione della luce.

Nel 1810 Malus pubblica le sue scoperte, in cui descrive il comportamento della riflessione e rifrazione su diversi materiali tenendo conto di questo nuovo concetto delle onde polarizzate. I suoi risultati sono corretti per quanto riguarda l'acqua, ma non per il vetro; ma non per colpa sua: a quei tempi il vetro non veniva ancora prodotto con le necessarie caratteristiche di precisione ottica (in particolare, molte lastre di vetro dell'epoca esibivano un diverso coefficiente di rifrazione sulle superfici rispetto al loro interno).

Il testimone passerà ad altri eminenti personaggi, di cui parlerò nella prossima puntata. Resta comunque aperta la questione di fondo: di cosa è fatta la luce? Corpuscoli od onde? Gli scienziati erano ancora convinti di poter spiegare tutto in base ai corpuscoli, poiché ormai era chiaro che fosse impossibile farlo con le onde longitudinali. D'altra parte le onde trasversali ponevano una quantità di problemi teorici, a partire dal mezzo in cui si propagano. Come già accennato nella puntata precedente, il cosiddetto "etere luminifero", per consentire alle onde trasversali di viaggiare alla velocità della luce, avrebbe dovuto essere più rigido dell'acciaio; ma questo etere non rivelava la propria presenza in nessun tipo di esperimento scientifico a parte di quelli ottici. ▲

Esperimenti fatti in casa

Materiale occorrente:

— un cristallo di spato d'Islanda. Si trova nei negozi di minerali, costa intorno alla decina di euro.

— un filtro polarizzatore per macchina fotografica.

— un puntatore laser. Non lo vendono più come giocattolo, ma lo si trova nei negozi di articoli per ufficio; se ne trovano al prezzo di un'altra decina di euro.
Attenzione: non puntare mai il laser direttamente negli occhi, né propri né altrui!

Il primo esperimento consiste nel sistemare il cristallo di calcite su una scritta stampata, ottenendo un effetto di sdoppiamento simile a quello di cui ho parlato qui sopra. Sovrapponendo il filtro polarizzatore al cristallo, e facendolo ruotare, si vede un effetto di questo genere:

La luce che illumina la scritta passa attraverso il cristallo dividendosi in due fasci a diverse polarizzazioni, ortogonali fra loro. Il filtro consente di vederne uno solo per volta, quando l'allineamento fra il piano di polarizzazione di uno dei fasci e il filtro sono perfettamente coincidenti, oppure entrambi i fasci quando il filtro è ruotato in una posizione intermedia fra gli angoli di polarizzazione dei due fasci di luce.

Secondo esperimento: invece di sfruttare la luce ambientale, usiamo un raggio laser in una stanza buia. Per fare le foto che seguono ho sistemato le cose in questo modo:

Il raggio di luce generato dal puntatore laser A viene fatto passare attraverso il filtro polarizzatore B; poi, attraverso la maschera C dotata di un piccolo foro circolare (l'uscita del mio raggio laser non è perfettamente puntiforme, e ha bisogno di essere "ritagliato"), raggiunge il cristallo D per proiettarsi sullo schermo E. (Ringrazio la signora aldoaldoz per avermi concesso in prestito d'uso le mollette da bucato, indispensabili per tenere acceso il puntatore laser e per tenere al loro posto tutti gli oggetti mostrati nella fotografia).

Ecco il risultato dell'esperimento:

In basso tre foto della luce proiettata sullo schermo, fatte con un diverso orientamento del filtro polarizzatore; in alto, il cristallo fotografato durante l'esperimento: si vede qualche alone di luce rossa, dovuto a fenomeni di diffrazione che si manifestano sulle superfici del cristallo. ▲

Prossimo capitolo: Interferenza

Ottica: Dispersione e telescopio di Newton

Sommario:

+ Introduzione
+ Riflessione
+ Rifrazione
+ Diffrazione
+ Aberrazione sferica e Cannocchiale
– Dispersione e Telescopio di Newton
      Isaac Newton
      Il prisma
      Aberrazione cromatica
      Il telescopio di Newton
      Controversie scientifiche
      Specchi liquidi
+ Etere Luminifero
+ Birifrangenza e Polarizzazione
+ Interferenza
+ L'arcobaleno

Isaac Newton

Come dicevo alla fine del capitolo precedente, "per fortuna"... nel 1665 a Londra scoppiò la peste, propagandosi in breve tempo fino a Cambridge: l'università locale (il celebre Trinity College) venne evacuata, e Isaac Newton dovette tornare nella sua città natale, in solitudine quasi completa.

Nato già orfano di padre il 4 gennaio del 1643 (secondo il nostro "nuovo" calendario gregoriano, oppure il 25 dicembre del 1642 secondo il vecchio calendario giuliano allora in vigore in Inghilterra: in effetti molti biografi preferiscono la seconda di queste due date, per sottolineare la coincidenza per cui Newton sarebbe nato nello stesso anno in cui moriva Galileo!), la madre si risposò dopo tre anni con un uomo che Isaac odiava cordialmente. La sua infanzia fu molto infelice, cosa che lo segnò per tutta la vita: di carattere ombroso e scorbutico, pare che egli abbia riso una sola volta in vita sua, quando un suo studente gli chiese se valesse la pena studiare gli "Elementi" di Euclide!

Newton frequenta il Trinity College dal 1661 con il titolo di subsizar (servitore): era la qualifica degli studenti poveri, che si guadagnavano la retta servendo a tavola e facendo le pulizie. Nel 1669 diverrà "Professore Lucasiano" (cioè titolare della cattedra di matematica fondata pochi anni prima da tale Henry Lucas) nello stesso college.

Ma torniamo all'anno 1665 e all'esilio di Newton. In quell'anno esprime il suo genio al massimo grado, avviando lo sviluppo dell'analisi matematica, studiando la meccanica e le tre famose leggi della dinamica, e intuendo la legge di gravitazione universale. In questo stesso anno acquista un oggetto che al momento non ha alcun uso pratico, ma che serve per sorprendere la gente nelle fiere: un prisma di vetro. ▲

Il prisma

Newton aveva già letto tutti gli studi precedenti sull'ottica, scritti da personaggi come Cartesio, Fermat, Galileo, Copernico, Keplero... quindi sapeva cosa doveva aspettarsi. Praticò un buco nella persiana, e fece passare uno stretto fascio di luce solare attraverso il prisma. Ciò che ottenne assomiglia a quest'immagine (si tratta di una simulazione molto accurata fatta al computer, che fa vedere il raggio di luce nel suo percorso anche se in realtà esso risulterebbe visibile solo in presenza di vapore, o fumo o polvere).

Il raggio bianco che arriva da sinistra viene rifratto due volte, e rimane bianco se non per due leggere striature, blu nella parte alta e rossa nella parte bassa del fascio luminoso, sulla destra. La proiezione del fascio su di uno schermo bianco posizionato vicino al prisma dà come risultato una cosa del genere:

Anche qui si vedono le due striature, blu e rossa. Il fenomeno del cambiamento di colore nella luce era cosa nota dall'antichità: infatti la luce che si riflette su un corpo colorato si colora anch'essa. L'idea era che la luce "pura" fosse solo quella bianca (come la vediamo provenire dal Sole e dalle Stelle); e che la materia con la quale interagiva in qualche modo la "sporcasse": insomma fino agli studi di Newton c'era la convinzione che i fenomeni di alterazione dei colori da parte di lenti e prismi fossero dovuti alla materia "impura" di cui erano fatti.

Newton però compie nuovi esperimenti nei quali allontana sempre più lo schermo dal prisma:

Ecco che il fascio di luce bianca via via sparisce, per far posto a bande dai colori ben definiti. Ma questo è un fenomeno molto più graduale di quanto si pensi normalmente: tutto il contrario di quanto rappresentato nella copertina di questo celeberrimo disco (The dark side of the Moon, dei Pink Floyd):

Newton ripete i propri esperimenti in mille modi diversi, ottenendo risultati sempre analoghi: la macchia di luce bianca si allunga senza mai allargarsi, e la sequenza dei colori è sempre la stessa, con il colore viola-blu sempre dal lato della rifrazione più angolata. Comincia a pensare che non ci sia in gioco solo un "inquinamento" più o meno casuale della luce, dovuto solo al materiale che attraversa; piuttosto arriva alla conclusione che

La luce bianca è composta dai colori. Il prisma non modifica la luce bianca, ma la divide nelle sue componenti.

Per verificare questa teoria esegue due esperimenti cruciali. Ecco il primo:

Newton maschera il fascio di raggi rifratti dal prisma con uno schermo nel quale ha praticato un piccolo foro, in modo da "selezionare" un raggio monocromatico, cioè costituito di luce di un solo colore. Ebbene, per quanti esperimenti faccia su questo raggio di luce, non riuscirà più a fargli cambiare colore. Ovvero confuta la tesi secondo cui è il vetro a colorare la luce: se i raggi di luce di ogni singolo colore possono attraversare il secondo prisma senza che il colore ne risulti alterato, vuol dire che la luce "pura" è quella dei singoli colori mentre la luce bianca è un miscuglio degli stessi colori.

Il secondo esperimento dovrebbe secondo Newton tagliare la testa al toro: usando una lente e un secondo prisma riesce a ricombinare la luce uscente dal primo prisma un un nuovo raggio di luce bianca.

Quest'immagine ha proporzioni falsate: abbiamo già visto che i raggi colorati divergono di pochissimo all'uscita del prisma. Per compiere quest'esperimento Newton ha bisogno di un laboratorio di molti metri... insomma, molto più grande di questo schermo!

La luce esce dal primo prisma sotto forma di raggi colorati che divergono; la lente li fa riconvergere a ridosso del secondo prisma: se quest'ultimo non fosse presente, i raggi proseguirebbero in linea retta riaprendosi a ventaglio con l'ordine dei colori invertito (il rosso in alto).

Il prisma invece riunisce tutti i raggi colorati in unico fascio di luce bianca. Per Newton il risultato dell'esperimento è chiarissimo: le vecchie teorie che indicavano i colori della luce come un inquinamento della luce bianca sono false; infatti come si sarebbe potuta ottenere una "pura" luce bianca, dopo un processo che la dovrebbe avere così tanto sporcata? ▲

L'aberrazione cromatica

Questi esperimenti di Newton portano alla definizione di un nuovo tipo di aberrazione: dopo l'aberrazione sferica di cui abbiamo parlato nella puntata precedente, adesso siamo in presenza dell'aberrazione cromatica, cioè della non omogenea rifrazione di tutti i colori della luce bianca.

Newton si convince che, se anche si potessero realizzare lenti perfette in grado di annullare completamente l'aberrazione sferica, non sarà mai possibile annullare l'aberrazione cromatica: ecco la spiegazione di quegli immancabili aloni colorati che continuano a disturbare lo studio del cielo anche usando i migliori telescopi! In realtà il problema dell'aberrazione cromatica sarà risolto verso la metà del XVIII secolo grazie all'uso di coppie di lenti costruite con vetri caratterizzati da indici di rifrazione diversi. ▲

Il telescopio di Newton

Nel 1663 James Gregory aveva ipotizzato la costruzione di un telescopio a riflessione, dotato di soli specchi. Newton, che aveva verificato come la riflessione, al contrario della rifrazione, non desse mai problemi di aberrazione cromatica, rispolvera questa idea, la perfezione e realizza un primo telescopio a riflessione: ha uno specchio principale di forma parabolica, uno specchio piano e un oculare.

La luce proveniente da sinistra (raggi blu) viene riflessa dallo specchio principale. I raggi riflessi (in rosso) convergerebbero verso il punto F... ma l'interposizione dello specchio secondario 2 rinvia i raggi (in verde) all'esterno del telescopio, nel punto O. Con l'opportuna scelta della forma dello specchio principale (parabolica, ne parlo qui di seguito), si ottiene per incanto uno strumento che non risente né dell'aberrazione sferica né di quella cromatica!

Fra le altre cose, Newton è anche un valentissimo artigiano: costruisce vari telescopi di questo nuovo tipo molando gli specchi da sé, e ne presenta uno alla Royal Society di Londra nel 1668. Lo strumento è stupefacente: pur essendo un oggetto molto semplice e di dimensioni contenute, fornisce immagini migliori di qualsiasi telescopio fosse stato costruito in precedenza! ▲

Controversie scientifiche

Nel gennaio del 1672 Newton viene eletto membro della Royal Society (ne diverrà presidente nel 1703). Il successo raggiunto lo spinge ad osare: una settimana dopo la sua elezione, invia al segretario di questa stessa Accademia Inglese delle Scienze, Henry Oldenburg, una lettera in cui annuncia di avere compiuto una

scoperta filosofica, che a mio giudizio è la più strana se non la più considerevole, che sia stata compiuta finora nelle operazioni della natura.

Possiamo immaginare il fastidio di Oldenburg nel ricevere una lettera siffatta da questo arrogante giovane (trentenne), così terribilmente ambizioso!

Poche settimane dopo Newton invia per la pubblicazione sulle Transactions of the Royal Society un articolo in cui espone la sua rivoluzionaria teoria dei colori. Sostiene che con un solo esperimento pratico si può fornire la prova decisiva a favore della sua nuova teoria dei colori, a scapito delle ormai consolidate teorie modificazioniste: proprio l'esperimento dei due prismi, con cui si scompone e ricompone la luce bianca. Infine spiega i suoi risultati con una teoria di tipo corpuscolare: la luce bianca sarebbe una miscela di corpuscoli differenti che si propagano nello spazio come proiettili che si muovono a velocità diverse...

Con grande disappunto di Newton, l'articolo non viene accettato. Sottoposto ad altri scienziati dell'epoca, riceve tre ordini di critiche: alcuni non riescono a replicare l'esperimento; altri non negano il risultato dell'esperimento, ma l'interpretazione data da Newton; altri ancora (in particolare Huygens) sostengono che la scoperta di Newton sia di poca importanza: sarebbe solo la scoperta di una diversa frangibilità della luce in base ai colori, non certamente la prova definitiva a sostegno di una qualsiasi teoria sulla natura della luce.

La difficile replicabilità dell'esperimento di Newton è giustificata dal fatto che nell'articolo inviato alla Royal Society la sua descrizione è molto sommaria, e non pone sufficientemente l'accento sulla precisione con la quale devono essere realizzati i prismi. Inoltre c'era diffidenza verso un personaggio semisconosciuto che sosteneva che una sola esperienza potesse confutare i moltissimi "studi" fatti in precedenza: insomma in Europa vengono fatti vari tentativi di replicare l'esperimento, ma senza raggiungere un consenso diffuso né sui risultati né tanto meno sulle loro interpretazioni. Nel marzo del 1675 viene programmata l'esecuzione dell'esperimento proprio presso la Royal Society ma, per l'appunto, quel giorno il sole non c'è: piove a dirotto! Finalmente l'esperimento verrà fatto con pieno successo il 27 aprile del 1676; il mondo scientifico si convincerà della validità dei risultati...

... ma non delle interpretazioni sulla natura della luce, ovvero dei meccanismi che giustificherebbero questo suo comportamento. Nella puntata precedente abbiamo visto che si stava diffondendo la teoria ondulatoria: proprio Huygens chiederà chiarimenti a Newton su qual è secondo lui il peso del suoi risultati nell'appoggiare la teoria corpuscolare rispetto a quella ondulatoria.

La controversia fra i sostenitori delle teorie corpuscolare e ondulatoria continuerà a lungo, anche perché vengono osservati sempre nuovi fenomeni. In particolare Robert Hooke (1635-1703), stava continuando a sviluppare la teoria ondulatoria della luce occupandosi di nuovi fenomeni come l'interferenza. Nello scambio di lettere fra Hooke e Newton, a un certo punto quest'ultimo scrive:

Se ho visto più lontano, è perché stavo sulle spalle di giganti.

Sebbene questa frase appaia come segno di modestia (nei confronti di Cartesio, Galileo, ecc.), alcuni ritengono che si trattasse si una punzecchiatura: Hooke infatti era un uomo particolarmente basso di statura!

A lungo andare Newton, offeso dalla perdurante mancanza di riconoscimento delle proprie teorie (la modestia non faceva proprio parte del suo carattere), si ritira dalla disputa giurando in cuor suo di non pubblicare mai più alcun risultato scientifico. Già nel 1675 scrive ad Oldenburg:

Desidero evitare di essere coinvolto in tali fastidiose dispute prive di significato...

Per fortuna poi le cose non andranno davvero così: nel 1687 pubblicherà il celeberrimo e fondamentale "Philosophiae Naturalis Principia Mathematica". ▲

Specchi... liquidi

La parabola è una curva nota dall'antichità, grazie ai primi studi di Apollonio da Perga che scrisse un trattato sulle "Coniche", la famiglia di curve di cui la parabola fa parte.

Durante le sue lunghissime ricerche sul moto dei pianeti, Keplero studiò queste curve, arrivando a un risultato di notevole interesse per l'astronomia: raggi di luce che arrivino su una superficie parabolica, in direzione parallela all'asse della parabola stessa, vengono riflessi in modo da convergere esattamente in un punto, detto fuoco (il nome "fuoco" di questo punto è stato assegnato proprio da Keplero):

Questa superficie quindi si presta perfettamente alla costruzione dei telescopi, infatti non presenta né aberrazione sferica (dovuta alla forma delle lenti) né cromatica (lo specchio non disperde la luce bianca).

Ecco che il paraboloide, ovvero la superficie che si ottiene facendo ruotare una parabola lungo il suo asse di simmetria, è proprio la forma ideale per costruire lo specchi primario di tutti i telescopi a riflessione: infatti non presenta né aberrazione sferica (dovuta alla forma delle lenti) né cromatica (lo specchio non disperde la luce bianca). Questa forma è la stessa delle antenne satellitari: infatti anche in questo caso le onde elettromagnetiche, che provengono da oltre 30000 km di distanza, sono sostanzialmente parallele fra loro. La parabola le riflette concentrandole nel punto in cui è montato il cosiddetto "illuminatore", ovvero l'elemento sensibile dell'antenna.

Con questo tipo di specchio sono stati costruiti i più grandi telescopi al mondo: il record spetta al Gran Telescopio Canarias (GTC), con uno specchio primario di 10,4 metri. Il famoso Telescopio Spaziale Hubble ha uno specchio primario di "soli" 2,4 metri... ma ha il non trascurabile pregio di essere in orbita, quindi di non risentire dei disturbi causati dall'atmosfera terrestre.

Adesso una domanda: Ma come diavolo si fa a molare uno specchio di 10 metri in modo da ottenere la forma di un paraboloide? Qui ci viene ancora in aiuto (guarda caso!) proprio Newton. Il quale scoprì che prendendo un secchio pieno d'acqua, e facendolo girare intorno al suo asse verticale, la superficie dell'acqua si dispone proprio a forma di paraboloide. Ecco un esempio pratico, che ho realizzato attaccando un contenitore di plastica al mandrino di un trapano mediante tre fili (l'acqua è leggermente colorata con inchiostro di china per rendere l'effetto più visibile); potete vedere un breve filmato di quest'esperienza se cliccate sulla foto qui sotto:

In estrema sintesi, il procedimento per fabbricare uno di questi enormi specchi è il seguente:

— All'interno di una camera a vuoto di opportune dimensioni si installa uno "stampo" (come quello delle torte), che girerà su se stesso a velocità costante, nell'ordine di pochi giri al minuto;

— facendo il vuoto (in modo da evitare il formarsi di bolle d'aria) viene versata un'opportuna quantità di vetro ottico fuso;

— inizia una fase molto graduale di raffreddamento: ci può volere più di un anno per portare il vetro a temperatura ambiente (solo così si possono evitare tensioni dovute alla non omogenea contrazione del vetro durante il raffreddamento);

— a questo punto la superficie del vetro è quasi perfetta: basta una lucidatura (di estrema precisione);

— applicando nuovamente il vuoto, si procede alla metallizzazione della superficie dello specchio, e il gioco è fatto!

Il "trucco" di far ruotare lo stampo per ottenere una superficie parabolica si presta anche ad un altro uso: la realizzazione di "specchi liquidi". Ne esistono vari al mondo, fino a 6 metri di diametro e oltre: è sufficiente mantenere in rotazione una forma e versarci del mercurio.

Naturalmente questo tipo di specchio può essere disposto solo con l'asse di rotazione verticale; inoltre i problemi di sospensione e di attivazione della rotazione sono tutt'altro che semplici da risolvere: non ci devono essere vibrazioni né le minime variazioni di velocità, pena veder comparire delle onde o increspature sulla superficie. Cionondimeno, i costi di realizzazione di uno specchio liquido sono circa un decimo rispetto al costo di uno specchio solido, a parità di diametro. ▲

Prossimo capitolo: Etere Luminifero