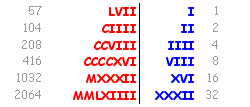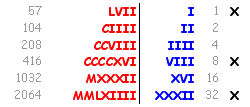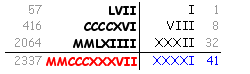+ Contare
+ Sistemi di numerazione
+ Addizione e Sottrazione
+ Moltiplicazione
– Divisione
L'uomo primitivo
L'antico Egitto
I Babilonesi"
I numero Romani: l'Abaco
I "Bastoncini di Nepero"
I Numeri Razionali
Numeri Decimali Periodici
La Frazione Generatrice
Curiosità storiche
+ Radice Quadrata
+ Elevamento a potenza
+ Logaritmi
+ Il Regolo Calcolatore
L'uomo primitivo
Fra i nostri antichissimi progenitori sicuramente abbiamo avuto qualche uomo primitivo dedito alla caccia e alla raccolta. Il quale, trovandosi sotto a un melo e avendo raccolto sette mele belle mature, se ne torna a casa tutto contento.
A casa ci sono moglie e figlia, per cui bisogna fare le parti, anche se è probabile che l’uomo le abbia mangiate tutte lui, dandone forse solo una a ciascuna delle sue donne. Ma ammettiamo che l’uomo fosse equo: non avrà certo detto:
Ecco, donne: tenete ciascuna le vostre due virgola tre periodico mele!Avrà semplicemente dato loro due mele e un terzo. In questo senso avrebbe certamente ragionato con i numeri naturali: due mele (numero naturale) e un (sempre numero naturale) terzo di mela: le parti di mela (terzi) le avrebbe considerate come unità di pezzi di mela. ▲
L'antico Egitto
Spostiamoci nell'antico Egitto. Per il pranzo della domenica in famiglia, la cuoca ha preparato una torta da dividere fra babbo, mamma e tre figli. La torta viene presentata in tavola già divisa in cinque fette, ma la figlia maggiore è a dieta, e il figlio minore si impossessa immediatamente della fetta in più. Domanda: quanta torta ha mangiato il figlio minore?
La risposta ovvia sarebbe "due quinti", ma per l’antico egizio non era così. Il valore trovato di 2/5 avrebbe avuto bisogno, per un egizio antico, di un’ulteriore "semplificazione": per loro una frazione aveva significato solo se al numeratore c’era il numero uno. Quindi:

In questo papiro, datato circa 1700 a.C., che ne ricopia un altro precedente di altri 100 anni, c’è una tabella di conversione di tutte le frazioni del tipo 2/N in somme di frazioni unitarie; e questo per tutti i numeri N dispari compresi fra 5 e 101. Faccio un paio di esempi:
Contenti loro. Certo, fossi andato io a scuola a quei tempi credo che mi sarei buscato un 2 meno meno, perché avrei detto semplicemente che:
I Babilonesi
Contemporanei agli Egizi, i Babilonesi risolsero alcuni problemi in un modo tanto geniale che ne approfittiamo ancora oggi. Qualsiasi calcolo frazionario veniva fatto non con l’unità al numeratore, ma con il numero 60 al denominatore (per esempio la torta egiziana sarebbe stata divisa in 60 parti: 12 parti ciascuno; ma siccome il figlio minore ne mangia due parti, a lui toccano 24/60 di torta).
In una tavoletta babilonese contemporanea al papiro egizio di cui sopra, c’è una tabella di conversione per il calcolo dei reciproci (ovvero, dato un numero N, calcolare il valore di 1/N). Alcuni esempi:
in cui alla destra dell'uguale è indicato il numero di “sessantesimi”. Occhio all’ultima frazione a destra: cosa significa 7,5? I decimali non potevano esistere… quindi i babilonesi si sono inventati una seconda “cifra” decimale. Il risultato veniva scritto:
in cui il 7 sta per sette sessantesimi, il 30 per trenta sessantesimi di sessantesimo, cioè:
Come ho spiegato qui, il sistema di numerazione babilonese prevedeva un gruppo di simboli per la numerazione da 1 a 60; in più fu inventato anche lo zero. I numeri venivano scritti con più "cifre", prelevando sempre dallo stesso gruppo di simboli. In altre parole, erano in grado di scrivere numeri di quante cifre volessero, utilizzando sempre gli stessi simboli. Per esempio il numero 253,125 per i babilonesi si sarebbe scritto 4 13 7 30:
L’unica cosa che non avevano introdotto nel loro sistema di numerazione era un metodo chiaro per definire dove andasse messa la virgola decimale. Infatti il numero sopra potrebbe essere interpretato come 4, 13 7 30 oppure 4 13, 7 30 oppure 4 13 7, 30 oppure anche come un numero intero, senza "cifre" decimali (c'è da dire che la convenzione di usare la virgola decimale è una conquista della fine del XVI secolo...). Insomma la posizione della virgola andava capita dal testo in cui era scritto il numero.
Troppo complicato? Veramente è proprio ciò che facciamo noi tutti i giorni, ma utilizzando il 10 invece del 60. Esempio:
Utilizzare il 60 invece del nostro 10 credo che fosse solo questione di abitudine. Certo è che i babilonesi trovavano molti meno numeri periodici di noi: per noi già un semplice 1/3 vale 0,3 periodico; per loro valeva 0,20 (nel senso di 20 sessantesimi).
Qualche curiosità aggiuntiva: il sistema sessagesimale (così si chiama il sistema di numerazione in base 60) viene utilizzato ancora oggi nella misura del tempo (un’ora che vale 60 minuti, che valgono 60 secondi) e nella misura degli angoli (1 grado che vale 60 primi, che valgono 60 secondi). ▲
I numero Romani: l'Abaco
Ho già spiegato qui come ci si facevano le moltiplicazioni con l'abaco: ora è il turno delle divisioni.
Ammettiamo di voler dividere 256432 : 723. In relativamente pochi passaggi, e senza l'ausilio né di carta né di penna, si giunge velocemente al risultato. È il metodo usato anche quando l'unico sistema di numerazione diffuso in Europa era quello dei numeri romani... certo non ci sarebbe modo di calcolare con carta e penna una divisione espressa in questo modo:
______
CCLVIMCCCCXXXII : DCCXXIII
Quindi cominciamo da una parte. Nelle foto che seguono faccio vedere per chiarezza, passo per passo, il procedimento numerico; indico in blu le cifre importanti di ciascun passaggio, e le frecce accanto al pallottoliere indicano le righe sulle quale si sta operando.
Intanto riportiamo il dividendo sul pallottoliere, come mostrato nella figura di sinistra. Siccome l'operazione va eseguita per differenze successive, dobbiamo fare una prima sottrazione del divisore dalle cifre più significative del dividendo: allora occorre prendere in considerazione le prime quattro cifre, dato che altrimenti 723 sarebbe superiore a 256. A destra vediamo che sto sottraendo il 3 (cifra delle unità del divisore) dal 4 (cifra meno significativa del gruppo di 4 cifre):
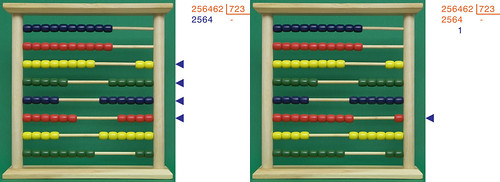
Proseguiamo sottraendo il 2 dal 5 (a sinistra) e il 7... dal 25: intanto aggiorno il pallottoliere mettendo 8 pallini, poi...
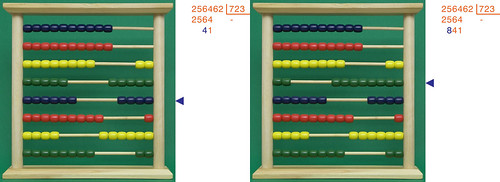
... faccio il riporto sulla cifra più significativa, che da 2 diventa 1 (a sinistra). Alla fine (a destra) sposto un pallino nella riga in alto, come promemoria del fatto che ho fatto la prima sottrazione:
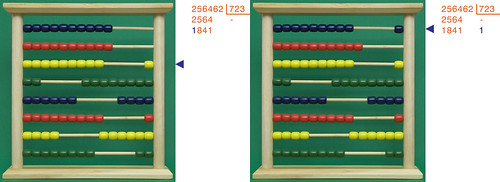
Con lo stesso procedimento vado avanti con le sottrazioni; vediamo che nella riga in alto i pallini spostati diventano prima 2 e poi 3:
A questo punto abbiamo finito con questa serie di sottrazioni, perché l'ultimo resto (395) è minore del divisore (723): allora la cifra più significativa del quoziente sarà un 3.
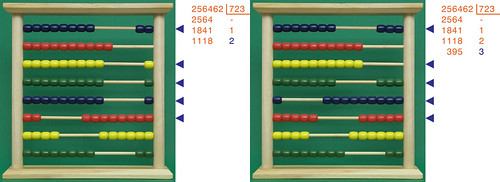
Ora "caliamo" il 6 dal dividendo (immagine a sinistra) e cominciamo con le sottrazioni da questo nuovo numero di 4 cifre; a destra si vede già il primo risultato, con il pallino spostato a destra nella seconda riga dall'alto:
Proseguiamo allo stesso modo...
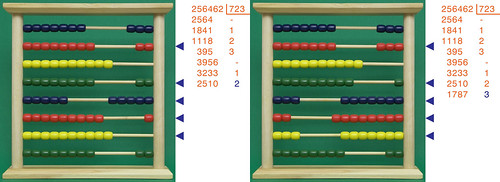

fino ad ottenere un resto minore del divisore, in questo caso 341. La seconda cifra del quoziente è quindi un 5.
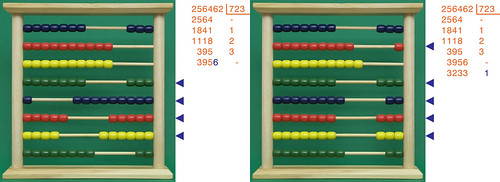
È il momento di "calare" l'ultima cifra del dividendo, il 2, e continuare con le sottrazioni:
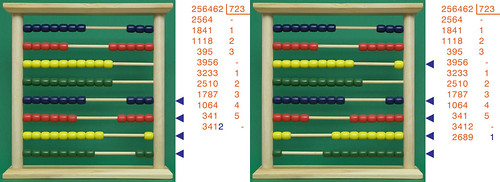
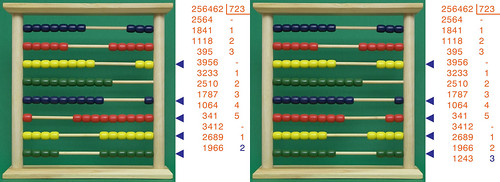
e finalmente esauriamo i calcoli da fare: nell'immagine di destra si vede chiaramente come la mia divisione dà come risultato 534, mentre il resto è 520:
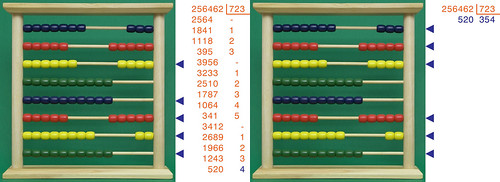
Per secoli questo è stato l'unico modo di calcolare divisioni. Non ha importanza se si usassero numeri romani o decimali: una volta trascritto il dividendo sul pallottoliere, tutti i calcoli venivano fatti solo sui pallini; il risultato finale poteva poi essere trascritto indifferentemente in numeri romani o decimali. ▲
I "Bastoncini di Nepero"
Vediamo invece come si potrebbe fare la stessa divisione con i bastoncini di Nepero (di qui ho già parlato qui, a proposito della moltiplicazione).
Si parte disponendo i bastoncini in modo da comporre il divisore con le cifre in alto (in questo caso, 723). Come ho già spiegato sopra, le cifre da gestire inizialmente del dividendo sono le prime quattro:
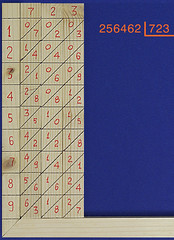
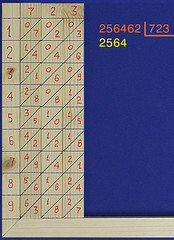
Con i bastoncini di Nepero è facile vedere qual è il più grande multiplo di 723 che sia inferiore a 2564: questo multiplo è 3 x 723, in quanto 4 x 723 darebbe 2892, troppo grande. Allora trascrivo il 3 e il prodotto di 3 x 723, poi calcolo la differenza (in basso a destra); infine "calo" la cifra successiva del dividendo:

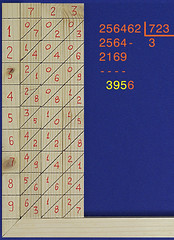
Ora ripeto il procedimento: il più grande multiplo di 723 che sia inferiore a 3956 è 5 x 723, in quanto 6 x 723 darebbe 4338, troppo grande. Allora trascrivo il 5 e il prodotto di 5 x 723, poi calcolo la differenza (in basso a destra); infine "calo" l'ultima cifra del dividendo:
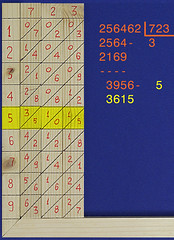
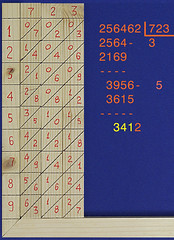
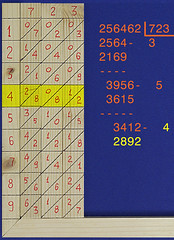
Ripeto per l'ultima volta il procedimento: l'ultima cifra del quoziente è 4; a destra il risultato: quoziente 534, resto 520.
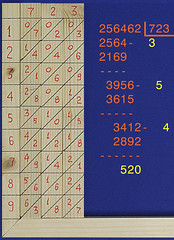
Quelli che ho descritto qui sopra sono stati i più diffusi mezzi "meccanici" per fare i calcoli aritmetici prima dell'invenzione delle macchine meccaniche. Lo sviluppo delle calcolatrici meccaniche è iniziato con Pascal ed è finito solo qualche decennio fa, con l'introduzione sul mercato delle prime calcolatrici elettroniche. ▲
I Numeri Razionali
L'aritmetica è nata storicamente per svolgere calcoli sui numeri naturali (numeri interi positivi, senza lo zero). Qualsiasi operazione di somma e moltiplicazione su tali numeri dà sempre come risultato un numero naturale: si dice infatti che il sistema dei numeri naturali "è chiuso" rispetto alle operazioni di somma e moltiplicazione.
La sottrazione invece può dare come risultato sia numeri negativi che lo zero: ecco comparire una nuova classe di numeri, quella dei "numeri interi relativi", o semplicemente dei "numeri interi", costituiti da tutti i numeri interi positivi, negativi e lo zero. Una volta introdotto questo nuovo sistema di numeri, si può dimostrare che esso è "chiuso" rispetto a alle operazioni di somma, sottrazione e moltiplicazione; queste operazioni, se fatte su numeri interi, possono dare come risultato solo altri numeri interi.
Negli esempi mostrati più sopra abbiamo calcolato divisioni fra numeri naturali che hanno dato un quoziente, ma anche un resto. Cosa significa questo resto che "avanza"? Che la divisione non è finita, ma potrebbe andare avanti alla ricerca delle cifre "decimali" dopo la virgola. La divisione quindi dà luogo a una nuova classe di numeri: i "numeri razionali".
I numeri razionali sono quelli che si ottengono dalla divisione o rapporto tra due numeri naturali (il termine "razionale" deriva dal latino "ratio", proprio nel suo significato di rapporto). Ogni numero razionale è il risultato di una divisione a / b in cui a è il numeratore e b il denominatore; b deve ovviamente essere diverso da zero, mentre se abbiamo b = 1 il risultato è un numero intero: i numeri interi (naturali) sono quindi un sottoinsieme dei numeri razionali. Analogamente a quanto fatto per i numeri interi, si può dimostrare che il sistema dei numeri razionali è chiuso rispetto a tutte e quattro le operazioni aritmetiche (mi fermo qui... perché di categorie di numeri ce ne sarebbero diverse altre!)
Il risultato di una divisione fra numeri interi può dare un numero intero (se il dividendo è multiplo del divisore) oppure altri due tipi di risultato:
— un numero decimale limitato (con un numero finito di cifre dopo la virgola)
— un numero decimale illimitato (numero infinito di cifre dopo la virgola)
Il tipo di risultato dipende dal divisore. Se una frazione ridotta ai minimi termini presenta al denominatore un numero composto solo dai fattori primi 2 e 5, il quoziente sarà un numero decimale limitato (questo dipende dal fatto che il numero 10, alla base della numerazione decimale, è divisibile sia per 2 che per 5); se invece il denominatore comprende altri fattori primi diversi da 2 e da 5, il risultato sarà un numero decimale periodico.
A questo proposito, voglio ora dimostrare due cose che ci hanno spiegato a scuola, e di cui forse non tutti sanno la spiegazione:
1 — Divisione fra numeri interi: se il risultato decimale è illimitato, è sempre periodico.
2 — A ogni numero decimale periodico può essere associata una frazione generatrice, ovvero quel rapporto fra numeri interi la cui divisione dà il numero periodico dato. ▲
Numeri Decimali Periodici
Vediamo il primo punto. Una volta fatta una divisione, se il resto è zero il quoziente è un numero intero e la divisione finisce qui. Altrimenti si può continuare il calcolo "calando" gli zeri, che ci consentono di trovare le cifre dopo la virgola. Anche qui, appena ottengo un resto uguale a zero il calcolo finisce. Facciamo un esempio con la divisione 13 : 40

Vediamo il calcolo di questa divisione riga per riga: nella riga A imposto la divisione; dato che il divisore è maggiore del dividendo, nella riga B scrivo lo "zero virgola" e nella C calo uno zero. Il 40 nel 130 ci sta tre volte, infatti nella riga D aggiungo la cifra 3 al quoziente e scrivo il 3 x 40 = 120. Nella riga E calcolo la differenza e calo un altro zero; proseguo così fino alla riga I: il resto zero pone fine alla divizione, il cui quoziente è 0,325.
Facciamo ora la divisione 1/6
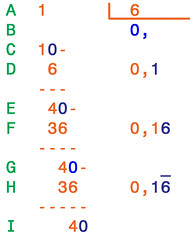
Anche in questo caso nella riga A imposto la divisione, nella B scrivo lo "zero virgola" e nella C calo uno zero. Il 6 nel 10 ci sta una volta: nella riga D aggiungo la cifra 1 al quoziente e scrivo il 6 x 1 = 6. Nella riga E calcolo la differenza e calo un altro zero; il 6 nel 40 ci sta 6 volte quindi aggiungo il 6 al quoziente, trascrivo il 6 x 6 = 36 e calcolo la differenza. La riga G riporta lo stesso resto che c'era al passaggio precedente (riga E): questo vuol dire che da ora in poi il procedimento si ripeterà all'infinito, così come si aggiungeranno all'infinito anche i 6 nel quoziente. Il quoziente infatti è 0,16, con il 6 periodico.
Finora abbiamo visto due casi: una divisione in cui a un certo punto il resto si azzera, e un'altra in cui il resto si ripete invariato, all'infinito. Ma quanti sono i diversi resti che posso ottenere mentre sto calcolando le cifre dopo la virgola? Ebbene: sono resti possibili tutti i numeri compresi fra uno e il valore del divisore diminuito di 1. Esempio: se il divisore è 7, i resti possibili sono solo 1, 2, 3, 4, 5 o 6. Allora è chiaro che prima o poi capiterà per forza di imbattersi in un resto già ottenuto in precedenza. Vediamo ora proprio la divisione 1 : 7

Concentriamoci sui resti: il primo che trovo (riga C) è un 1; poi (riga E) un 3, poi 2, 6, 4, 5 e infine (riga O) di nuovo un 1. Chiaramente da questo nuovo 1 riparte una sequenza identica a quella che ho appena descritto, e che si ripeterà all'infinito: quindi il quoziente ha un periodo di 6 cifre.
Ricapitolando: i quozienti possono essere interi, decimali limitati o illimitati; in quest'ultimo caso il periodo non può essere costituito da un numero di cifre superiore o uguale al numero indicato dal divisore. Ecco com'è che nessuna divisione potrà mai produrre un quoziente decimale illimitato ma non periodico. ▲
La frazione generatrice
Vediamo ora alla seconda questione lasciata in sospeso: perché a ogni numero decimale periodico può essere associata una frazione generatrice?
Se ricordate qualcosa dalle medie, ogni numero decimale poteva essere scritto in forma di frazione. Se il numero decimale è limitato come 0.125 basta creare una frazione in cui il numeratore è il numero dato senza la virgola, il denominatore è un 1 seguito da tanti zeri quante le cifre decimali: allora avremmo 125 / 1000 che, ridotto ai minimi termini, fa 1 / 8.
La regola per un numero decimale periodico semplice (come 0,57 con 57 periodico) è: scrivere una frazione in cui al numeratore si riporta il periodo (57) e al denominatore un numero composto da tanti 9 quante le cifre del periodo (99). Insomma la frazione generatrice di 0,57 periodico è 57 / 99: vediamo perché.
È semplice vedere che le divisioni 1 / 9, 1 / 99, 1 / 999 eccetera danno luogo a quozienti di questo tipo:

Calcolare 57 / 99 significa moltiplicare 57 per il reciproco di 99, quindi 57 per 0,01 con 01 periodico. Ecco qui il calcolo:

Da quanto sopra si vece che 57 x 0,01 periodico, che è come dire 57 / 99, dà proprio 0,57 periodico!
Per adesso mi basta "svelare" da dove saltano fuori quei 9 al denominatore della frazione generatrice; ma le cose si complicano un po' se ci troviamo davanti numeri con parte intera diversa da zero e/o antiperiodo (es. 12,425555... dove solo il 5 è periodico). Se poi la cosa vi interessa, diciamo che... non è impossibile ricavarle da quanto ho spiegato qui sopra!
Un'ultima curiosità: che razza di numero è lo 0,9 periodico? Presto detto:

0,9 periodico non è distinguibile dall'unità, quindi sono la stessa cosa! ▲
Curiosità stiruche
Una curiosità storica. Quand'è che si è cominciato a scrivere numeri decimali, nel senso non di numeri interi in notazione decimale, ma di numeri con cifre decimali dopo la virgola? Il primo a fare questo è stato il belga Simon Stevin o Simone di Bruges (1548-1620), noto anche come Simone Stevino. In una sua opera del 1585 descrive le operazioni aritmetiche su numeri scritti nella notazione decimale (anche se, curiosamente, non accettava l'esistenza di numeri decimali illimitati...). In questa pubblicazione compaiono numeri scritti in questo modo:
Le cifre nei cerchietti indicano le potenze di 10 da mettere al denominatore. Ecco in altre parole cosa rappresentano:
che semplificato è
e in notazione moderna vuol dire:
Il punto (o virgola) decimale è stato usato per la prima volta dal matematico, astronomo e teologo tedesco Bartholomaeus Pitiscus (1561-1613, quello che ha coniato il termine "trigonometria", a partire dal 1595, poi seguito dagli altri matematici come quel Nepero con cui abbiamo già avuto (e avremo ancora) a che fare. ▲
Prossimo capitolo: Radice Quadrata