Numeri Transfiniti: il Continuo

Sommario:

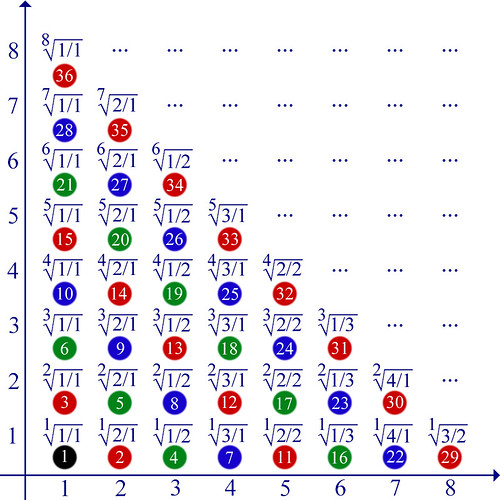
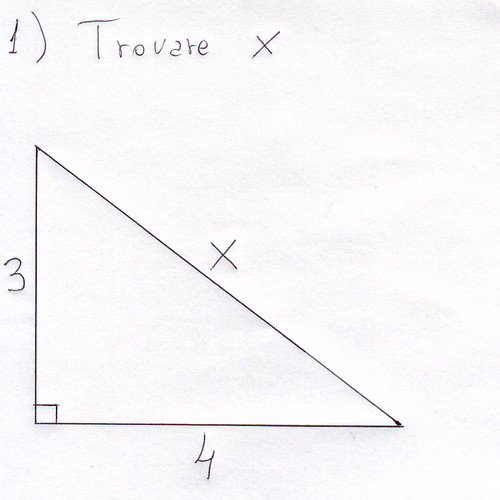
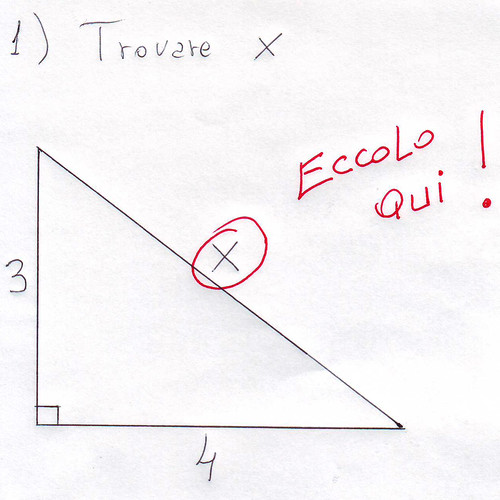
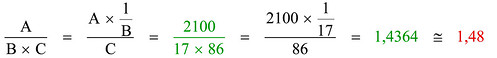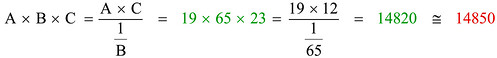+ I numeri Naturali
+ Ancora Aleph-zero
+ Il contesto storico
– Oltre Aleph-zero: il Continuo
      La Linea di Euclide
      La Retta dei numeri
      I numeri Trascendenti
      I numeri Reali
      Il "Continuo"
      Potenza del Continuo
      La dimostrazione di Cantor
+ L'ipotesi del Continuo

La Linea di Euclide

Un punto è ciò che è privo di parti

Credo che sia la più celebre definizione della geometria: è la prima fra quelle elencate da Euclide nei suoi "Elementi". Le successive tre invece sono:

Una linea è una lunghezza senza larghezza
Le estremità di una linea sono punti
La retta è quella linea che giace sui suoi punti in modo uniforme

Se fossi uno che non ne sa niente, non so se da queste definizioni, soprattutto la quarta, saprei immaginare cos’è una linea retta... meno male che tutti noi abbiamo almeno una volta tracciato una linea con righello e lapis! Però mi sembrano interessanti un paio di considerazioni:

— Una linea non solo "non ha larghezza", ma è fatta da punti "che sono privi di parti": questi punti sono quindi piccoli, piccolissimi, diciamo pure infinitesimali; se potessi tracciare una linea ideale, essa risulterebbe assolutamente invisibile!

— Il fatto che i punti siano privi di parti, fa sì che per costituire una linea continua tali punti debbano essere accostati l’uno all’altro con una densità estrema, pena il veder comparire dei "buchi". Vedremo in seguito ricomparire i concetti di densità e continuità.   ▲  

La Retta dei numeri

Lavorando con rette e numeri, Richard Dedekind (1831-1916) ha costruito una teoria rigorosa che ci limiteremo a descrivere in modo intuitivo: una retta può essere utilizzata per rappresentare tutti i numeri esistenti. In pratica si prende una retta (di lunghezza infinita), si traccia un punto che sarà l’origine al quale assegnare il valore zero; poi si stabilisce un segmento unitario, e riportandolo sulla retta quante volte su vuole, otteniamo a destra dello zero i numeri naturali positivi, a sinistra i numeri negativi.



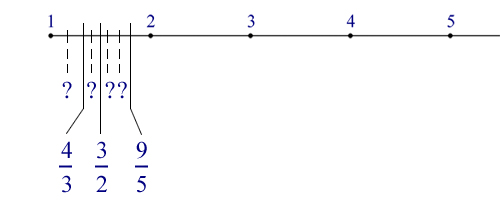
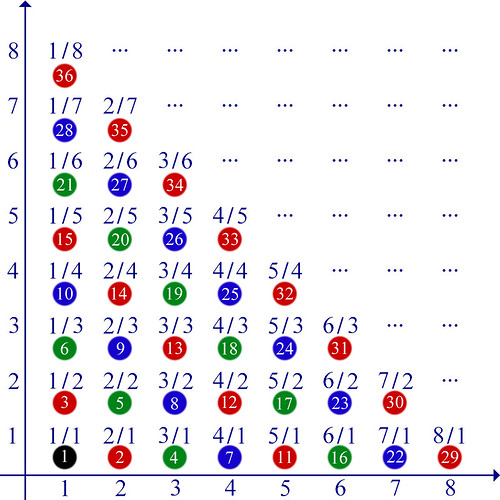
Naturalmente i soli punti identificati dai numeri interi non danno luogo a una linea continua, ma solo a una serie di punti ben spaziati l’uno dall’altro. Allora possiamo aggiungere i numeri razionali: dividendo ogni segmento unitario in n parti uguali, si ottiene la rappresentazione delle frazioni di denominatore uguale ad n; ripetendo l’operazione per ogni n, si ottengono infiniti punti della retta, che rappresentano numeri razionali.



Tali punti sono distribuiti in forma "densa", nel senso che tra due punti razionali qualunque esistono infiniti altri punti di tale tipo; infatti dati due punti P e Q qualunque è sempre possibile trovare un nuovo punto X compreso fra P e Q: basta fare la media: X = (P + Q) / 2. Questa operazione si può ripetere quante volte si voglia, quindi non ha proprio senso chiedere quanti punti razionali esistano nell'intervallo da essi marcato.

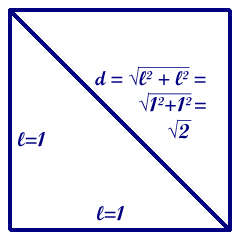
Tuttavia, per quanto densi, i numeri razionali non "riempiono" completamente la retta. Infatti, il punto R = radice di due è bensì rappresentabile sopra la retta (basta portare su di essa, a partire dall'origine, la diagonale del quadrato costruito sul segmento [0-1]. Esso però non è un razionale, come abbiamo dimostrato nei capitoli precedenti.



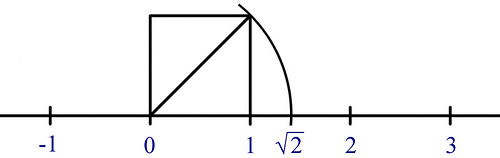
Usando metodi geometrici si possono tracciare sulla retta molti numeri irrazionali, ma non tutti. Per esempio è rimasto irrisolto, dai tempi dell’antica Grecia, il problema della "duplicazione del cubo": per fare questo sarebbe necessario determinare un segmento corrispondente alla radice cubica di due (la cosa si è dimostrata impossibile, almeno con l’ausilio dei mezzi elementari della geometria classica: la riga e il compasso).

Uno dei miti che circondano il problema della duplicazione del cubo è il seguente. Gli abitanti di Delo, interrogato l'oracolo di Apollo sul modo di liberarsi dalla peste, ricevettero l'ordine di costruire un altare, di forma cubica, dal volume doppio rispetto a quello esistente. Vista l’impossibilità di determinare con riga e compasso un segmento proporzionale alla radice cubica di due, questo altare non deve essere stato mai costruito; chissà allora gli abitanti di Delo come avranno fatto a liberarsi della peste...

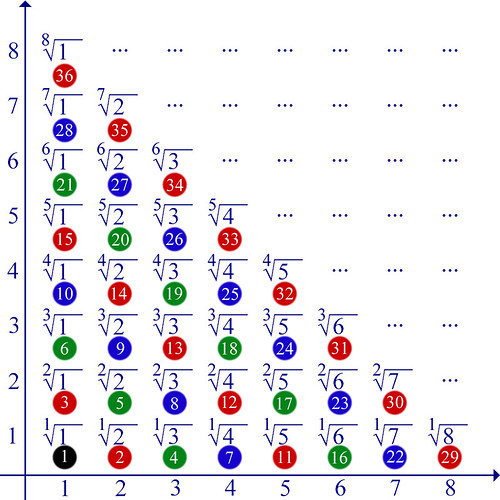
Indipendentemente dal fatto che molti punti non possano essere tracciare con i metodi classici, possiamo immaginare comunque di identificare sulla nostra retta tutti i numeri algebrici, ovvero quelli del tipo di cui abbiamo parlato nel capitolo precedente: sono quei numeri che si ottengono risolvendo una qualsiasi equazione polinomiale di qualsiasi grado. Ma neanche così riusciamo a coprire tutta la retta, infatti...   ▲  

I numeri Trascendenti

... esiste una classe di numeri detti "trascendenti", che sono gli irrazionali non algebrici. Il caso più noto è quello di pi greco: dall’antichità si cercava di capire che razza di numero fosse, e se si potesse fare la quadratura del cerchio (disegnare, con riga e compasso, un quadrato di area pari a quella di un cerchio dato). Ne parla anche Dante nel canto XXXIII del Paradiso:

Qual è ‘l geometra che tutto s'affige
per misurar lo cerchio, e non ritrova...

Insomma ce n’è voluto del bello e del buono, ma finalmente (solo!) nel 1882 Ferdinand von Lindemann (1852-1939) dimostrò la trascendenza di pi greco chiudendo definitivamente la questione della quadratura del cerchio. In quegli anni furono trovati molti altri numeri di questo tipo, anche se non è per niente facile dimostrarne la trascendenza.   ▲  

I numeri Reali

Finalmente possiamo definire una nuova classe di numeri: i cosiddetti numeri reali. È l’insieme di tutti i numeri, naturali, razionali, irrazionali e trascendenti. Come ho accennato, Dedekind ha dimostrato la possibilità di mettere in corrispondenza biunivoca i punti della retta con i numeri reali; siccome i punti della retta costituiscono qualcosa di continuo, anche i numeri reali identificano un insieme che possiamo definire "continuo".

Rimane però la questione se tutti questi numeri trascendenti, o meglio i numeri reali, possano essere ancora "contati" oppure no, ovvero se l’insieme dei numeri reali abbia cardinalità maggiore rispetto all’insieme dei numeri naturali.

Il problema è che non si può fare un elenco di tutti i possibili numeri trascendenti; alcuni sono i risultati del calcolo di funzioni trigonometriche, logaritmiche e altre cose del genere, ma a molti, a moltissimi altri non sapremmo neanche dare un significato matematico. Mi spiego meglio: se è vero che a un numero decimale periodico so sempre assegnare una frazione generatrice, quindi riesco sempre a capirne la natura, di un numero reale non posso sapere mai da quale espressione matematica è stato ricavato; per farlo dovrei conoscere tutti, ma proprio tutti i suoi infiniti decimali.

Faccio un esempio: se vedo il numero 3,14... a me viene subito in mente pi greco. Ma per sapere che questo numero è davvero pi greco dovrei conoscerne tutti i decimali, ma proprio tutti; basterebbe una cifra diversa alla miliardesima posizione decimale per farlo diventare qualcosa di diverso!

Insomma abbiamo trovato una nuova classe di numeri che è impossibile da catalogare. Saremo mica riusciti a trovare una classe di numeri che non sia più "contabile", ovvero tale da non poter essere messa in corrispondenza biunivoca con i numeri naturali?   ▲  

Il "Continuo"



La risposta finalmente è... Sì. Georg Cantor (1845-1918) ha trovato il modo per dimostrare che ci sono numeri che non possono essere contati. La dimostrazione dettagliata la fornisco più sotto, qui mi limito a descriverne il funzionamento. È una dimostrazione per assurdo: si immagina di avere stilato un elenco numerato di tutti i numeri reali compresi fra 0 e 1, ciascuno con i suoi infiniti decimali. Cantor riesce a creare un nuovo numero, diverso da tutti gli altri: in questo modo contraddice l’ipotesi di partenza (quella secondo cui ogni numero reale era rappresentato nell’insieme iniziale).

Eccoci al punto: abbiamo finalmente un insieme che non può avere cardinalità Aleph-0 perché ha almeno un elemento che sfugge al conteggio. All’insieme di tutti i numeri reali quindi si assegna la cardinalità c (la lettera c è stata scelta perché questo insieme indica il "continuo"). Per ora sappiamo che c è sicuramente maggiore di Aleph-0... ma gli sviluppi che conseguiranno da questa scoperta richiedono un intero capitolo di questa storia (il prossimo).   ▲  

Potenza del Continuo

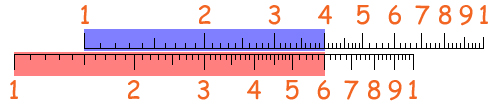
Cominciamo ad analizzare questo c. Intanto proviamo a vedere se un segmento lungo ha più punti di un segmento più corto: la risposta è no, in quanto si può sempre dimostrare la corrispondenza biunivoca fra i punti di due segmenti di lunghezza diversa (ciascun punto a del segmento [0-1] ha il suo corrispondente A nel segmento [0-2]).

#1


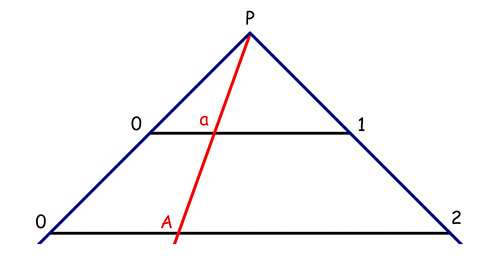
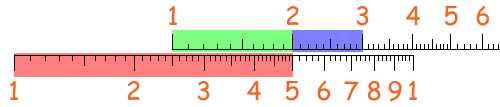
Proviamo ora a vedere se una retta di lunghezza infinita ha più punti di un segmento finito: un’altra volta la risposta è no, in quanto anche in questo caso si dimostra lo stesso tipo di corrispondenza. La dimostrazione si fa con il disegno qui sotto: si mettono in corrispondenza i punti di un semicerchio che ha centro in P con i punti della retta sottostante. A ogni punto del semicerchio corrisponde un punto della retta infinita: A-a, B-b, e C-c con c che evidentemente è ben fuori dal disegno, sulla sinistra.

#2


Ecco un risultato interessante: l’insieme dei punti di un segmento unitario (o l’insieme dei numeri reali nel campo [0-1]) ha la stessa potenza dei punti di una retta infinita (o dell’insieme di tutti i numeri reali).

Ma non finisce qui: proviamo a vedere se una superficie finita ha più punti di un segmento finito: ancora la risposta è no! Proviamo a considerare i punti di un quadrato unitario. Ogni suo punto può essere identificato da una coppia di coordinate X e Y comprese fra 0 e 1:

#3


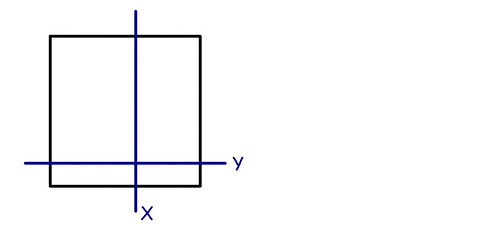
A partire dai numeri che definiscono le coordinate X e Y posso creare un nuovo numero R intercalando le cifre dei decimi, poi quelle dei centesimi, poi dei millesimi e così via. In questo modo avrò un unico numero che esprime la coppia di coordinate, anch’esso compreso fra 0 e 1: c’è quindi una corrispondenza biunivoca fra ciascuna coppia di coordinate e un numero reale. Faccio un esempio pratico:



Dal numero R riesco senza problemi a ricavare le due coordinate X e Y: le cifre decimali di ordine dispari di R daranno la coordinata X; le cifre di ordine pari la coordinata Y.

Ripetendo il metodo descritto dalla figura #2 per le superfici invece che per segmenti/rette posso dimostrare che c’è una corrispondenza biunivoca anche fra i punti di una superficie finita con i punti dell’intero piano infinito. E applicando il sistema dimostrato nel disegno #3 posso definire un nuovo numero R che, invece di partire da una coppia di coordinate X e Y, usi tre coordinate X Y e Z di uno spazio tridimensionale.

Allora c, il numero cardinale che indica la potenza del continuo, può essere utilizzato per definire la potenza degli insiemi di tutti i numeri reali, dei punti del segmento, della retta, del piano, dello spazio... eccetera eccetera!

La dimostrazione di Cantor

Descrivo qui la "dimostrazione diagonale di Cantor", con alcune semplificazioni per non appesantirne la lettura. Chi fosse interessato può leggere questo articolo su wikipedia.

Supponiamo per assurdo che l'intervallo dei numeri compresi fra 0 e 1 sia numerabile. Questo significa che gli elementi dell'intervallo possono essere posti in corrispondenza biunivoca con i numeri naturali dando luogo ad una successione di numeri reali R1, R2, R3, ... che esaurisce tutti i numeri reali compresi tra 0 e 1.

Possiamo rappresentare ciascun numero della successione in forma decimale e visualizzare la successione di numeri reali come una matrice infinita che avrà più o meno quest'aspetto:

R1 = 0 . 5 1 0 5 1 1 0 ...
R2 = 0 . 4 1 3 2 0 4 3 ...
R3 = 0 . 8 2 4 5 0 2 6 ...
R4 = 0 . 2 3 3 0 1 2 6 ...
R5 = 0 . 4 1 0 7 2 4 6 ...
R6 = 0 . 9 9 3 7 8 3 8 ...
R7 = 0 . 0 1 0 5 1 3 5 ...
...

In questa tabella ho indicate in grassetto le cifre che compaiono sulla diagonale (la prima cifra decimale del primo numero, la seconda del secondo, e così via). Costruiamo ora un nuovo numero reale X che abbia tutte le cifre differenti dalla sequenza sulla diagonale. Si procede nel seguente modo: se una delle cifre che compare sulla diagonale è 5, la sostituiamo con un 4; in tutti gli altri casi la sostituiamo con un 5 (la scelta delle cifre 4 e 5 è arbitraria). Nell'esempio otteniamo:

X = 0 . 4 5 5 5 5 5 4 ...

All'inizio dell'argomento avevamo supposto che la nostra lista dei numeri enumerasse tutti i numeri reali compresi tra 0 e 1, quindi dovremmo avere uno dei numeri R, diciamo l'ennesimo, per cui Rn = X. A questo punto emerge una contraddizione: per come abbiamo costruito il numero X, l'ennesima cifra di X dovrebbe essere diversa dall'ennesima cifra del numero Rn. Questo è impossibile, e ne segue che l'ipotesi di partenza è falsa e cioè che l'intervallo dei numeri compreso fra 0 e 1 non è numerabile.   ▲  

Prossimo capitolo: L'ipotesi del Continuo

Numeri Transfiniti: l'ipotesi del Continuo

Sommario:

+ I numeri Naturali
+ Ancora Aleph-zero
+ Il contesto storico
+ Oltre Aleph-zero: il Continuo
– L'ipotesi del Continuo
      Numeri transfiniti più grandi
      c & Aleph-uno
      L'ipotesi del Continuo
      Questioni... teologiche!

Riassunto delle puntate precedenti:

— La Cardinalità, o Potenza, dell’insieme dei Numeri Naturali si indica con la sigla Aleph-zero.
— Aleph-zero è il più piccolo Numero Transfinito.
— Esiste un insieme di numeri (i Numeri Reali) che ha Potenza maggiore di Aleph-zero: si tratta del "Continuo", che si indica con la lettera c.

Numeri transfiniti più grandi

Georg Cantor, nel Teorema che porta il suo nome, afferma che dato un insieme di qualsiasi potenza (ovvero contenente un numero qualsiasi di elementi), esiste sempre un insieme di potenza maggiore. Quindi da un punto di vista logico non c’è limite alla potenza o cardinalità degli insiemi infiniti: così come nei Numeri Naturali esiste sempre il successore di qualsiasi numero, anche da qualsiasi insieme infinito si riesce a ricavare un infinito "più grande"; e dato che la potenza degli insiemi infiniti viene identificata con i Numeri Transfiniti (Aleph-zero, Aleph-uno, Aleph-due e così via), è logico dedurre che i Numeri Transfiniti... sono infiniti anch’essi!

Vediamo da vicino questo Teorema di Cantor. Dato un insieme A, la dimostrazione viene fatta prendendone in esame le "parti", ovvero i possibili sottoinsiemi di A: questi ultimi saranno sempre in numero superiore rispetto agli elementi di A.

Iniziamo con un esempio semplice: diciamo che l’insieme A contenga due bocce, una rossa e una blu. Se ci venisse detto di prendere da questo insieme "le bocce che vogliamo", potremmo sceglierne una sola (la rossa o la blu), entrambe (la rossa E la blu), oppure potremmo decidere di non prenderne nessuna. Totale: quattro possibili "parti", o sottoinsiemi, a partire dall’insieme A di due elementi.

Allo stesso modo, se le bocce fossero tre, rossa blu e verde, potremmo sceglierne una soltanto (rossa o blu o verde), due (escludendo la rossa, la blu o la verde), prenderle tutte e tre oppure non prenderne nessuna. Totale: otto sottoinsiemi a partire da un insieme contenente tre elementi.

Le parti, o sottoinsiemi, di un insieme contenente n elementi, sono quindi sempre in numero di 2ⁿ. Infatti 2² = 4, 2³ = 8 (casi già visti); ma anche 2¹ = 2 (se l’insieme ha un solo elemento, possiamo prenderlo o non prenderlo). Infine 2º = 1: se l’insieme è vuoto, possiamo solo scegliere di prenderne una "parte" costituita da un altro insieme vuoto; comunque è una possibilità reale: insomma, da un insieme che ha 0 elementi si può sempre ricavare 1 sottoinsieme (vuoto).



In questa immagine sono rappresentati tutti gli insiemi di cui abbiamo parlato, di 0, 1, 2 e 3 elementi, i cui contenuti sono indicati fra le parentesi graffe in nero; il numero in nero alla loro sinistra indica la potenza, o cardinalità, dei rispettivi insiemi.
I numeri in grigio a destra della riga verticale indicano il numero delle Parti, o dei possibili sottoinsiemi, degli insiemi suddetti: ciascun sottoinsieme è racchiuso fra parentesi graffe di colore nero, mentre le parentesi graffe di colore grigio indicano che ogni espressione a destra della riga nera verticale rappresenta un insieme di insiemi.

Ricapitoliamo quanto detto finora: nessun insieme finito può essere messo in corrispondenza biunivoca con l’insieme delle sue parti (sottoinsiemi), poiché le parti sono sempre in numero maggiore degli elementi dell’insieme.

Resta ora da capire se questo sia vero anche per gli insiemi infiniti. Sembrerebbe ovvio dire di sì; ma abbiamo già visto come, quando si ragiona di infinito, non si può dare niente per scontato: infatti i soli numeri pari, o i fattoriali e qualsiasi altra serie infinita di numeri apparentemente meno numerosi; e i numeri razionali, i numeri algebrici e altre serie via via "più numerose", hanno tutte la potenza dei Numeri Naturali, ovvero danno tutti luogo a insiemi equipotenti di cardinalità Aleph-zero. Non potrebbe allora essere che abbia la stessa cardinalità anche l’insieme delle parti (sottoinsiemi) dei Numeri Naturali? Ovvero, non sarà che le parti di un insieme di potenza Aleph-zero possano essere tranquillamente contate?

La dimostrazione di Cantor è assolutamente simbolica (direi "astratta"): per far capire come funziona ne illustro solo un esempio "pratico", più facilmente comprensibile.

Ammettiamo di creare l’insieme B di tutti i possibili sottoinsiemi dei Numeri Naturali A, e di averli messi in corrispondenza biunivoca con i Numeri Naturali stessi. La cosa potrebbe essere così:

A — B
-----------------------------------
1 — { 1, 2 }
2 — { 3, 5, 6 }
3 — { 7 }
4 — { 1, 2, 4, 8, 9 }
5 — { 2, 6, 7 }
6 — { 5, 6, 7, 8 }
....................................

A sinistra l’insieme dei Numeri Naturali (identificato in alto dalla lettera A); a destra l’insieme (identificato dalla lettera B) di tutti i possibili sottoinsiemi di A (le parentesi graffe come al solito indicano un insieme); i trattini indicano la corrispondenza biunivoca fra i membri degli insiemi A e B.

Possiamo ora creare un particolare sottoinsieme dei Numeri Naturali: questo dovrà contenere solo quei numeri che non sono presenti nel loro sottoinsieme corrispondente. Quindi (vedi la tabella sopra): il numero 1 è presente nell’insieme { 1, 2 } e non ne farà parte, mentre il 2 non è presente in { 3, 5, 6 }; allora i primi numeri di questo nuovo insieme saranno { 2, 3, 5 ... }.

Questo nuovo insieme, identifichiamolo con la lettera Z, contenendo solo Numeri Naturali, è un sottoinsieme dei Numeri Naturali stessi, quindi fa senz’altro parte di B (che è l’insieme di tutti i possibili sottoinsiemi dei Numeri Naturali), quindi deve comparire da qualche parte nell’elenco di destra della tabella mostrata sopra; di conseguenza, sarà anche associato a un qualche Numero Naturale, tra quelli presenti nell’elenco di sinistra: diciamo che tale numero sia Y.

Ora ci dobbiamo porre la seguente domanda: il numero Y fa o non fa parte dell’insieme Z, ovvero del suo insieme corrispondente?

— Se diciamo che Y è compreso in Z, in realtà non dovrebbe farne parte (per come è costruito Z);

— Se diciamo che Y non è compreso in Z, in realtà dovrebbe farne parte (per come è costruito Z).

Ecco quindi una contraddizione, che ci fa capire che il numero Y non può esistere. Allora esiste almeno un elemento B che non può essere messo in corrispondenza con un elemento di A: l’insieme B quindi ha potenza maggiore dell’insieme A.

Questo nuovo insieme ha cardinalità Aleph-uno; e da questo, applicando lo stesso procedimento, potremo ricavare altri insiemi di cardinalità Aleph-due, Aleph-tre... ecc..   ▲  

c & Aleph-uno

Ricapitoliamo:

— Aleph-zero è la cardinalità dell’insieme dei Numeri Naturali
— c è la cardinalità del Continuo
— Aleph-uno è la cardinalità dell’insieme delle parti di un insieme di potenza Aleph-zero

Domanda: che rapporto c’è fra c e Aleph-uno? Ebbene, si può dimostrare che rappresentano insiemi assolutamente equipotenti, quindi c = Aleph-uno.

Riprendiamo in esame gli insiemi definiti più sopra: A (dei Numeri Naturali) e B (delle parti, o sottoinsiemi, dei Numeri Naturali stessi). Ogni elemento di B è un insieme costituito da uno, o più (o tutti, o nessuno) elemento di A. Associando a ciascuno dei possibili elementi di un sottoinsieme di B due valori: 0 – assente, 1 – presente, possiamo tradurre gli esempi mostrati sopra nel seguente modo:

{ 1, 2 } — 110000000... (presenti solo primo e secondo elemento)
{ 3, 5, 6 } — 001011000... (presenti terzo, quindi e sesto)
{ 7 } — 000000100... (presente solo il settimo)
{ 1, 2, 4, 8, 9 } — 110100011... (presenti il primo, secondo, quarto, ottavo e nono)
................

Così come gli elementi di B erano tutte le possibili combinazioni (sottoinsiemi) degli elementi di A, così queste serie di cifre 0 e 1 rappresenteranno tute le possibili combinazione di zeri e uni, impacchettati in "stringhe" di lunghezza infinita.

Ora possiamo fare il passo conclusivo: davanti a queste stringhe di zeri e uni mettiamo un "zero-virgola".

0,110000000
0,001011000
0,000000100
0,110100011

Tutti questi possono essere intesi come numeri frazionari espressi nel sistema binario. A differenza dei numeri in notazione decimale, in cui la prima cifra dopo la virgola rappresenta i decimi, la seconda i centesimi, la terza i millesimi e così via, nei numeri binari la prima cifra rappresenta metà, la seconda un quarto, la terza un ottavo e così via. Quindi i numeri qui sopra valgono:

0,110000000 — 1/2 + 1/4 = 0,75
0,001011000 — 1/8 + 1/32 + 1/64 = 0,171875
0,000000100 — 1/128 = 0,0078125
0,110100011 — 1/2 + 1/4 + 1/16 + 1/256 + 1/512 = 0,818359375

Abbiamo convertito quindi tutti i possibili sottoinsiemi dei Numeri Naturali in tutte le possibili stringhe di lunghezza infinita di zeri e uni. Nella loro rappresentazione binaria, queste stringhe di zeri e uni rappresentano ogni possibile Numero Reale compreso fra zero e uno: ecco quindi com’è che la potenza, o cardinalità, dell’insieme delle Parti (sottoinsiemi) dei Numeri Naturali è esattamente la stessa del Continuo, ovvero dell’insieme di tutti i Numeri Reali compresi fra zero e uno.   ▲  

L'ipotesi del Continuo

Adesso viene una domanda molto interessante. Siamo sicuri che questi numeri trasnfiniti c = Aleph-uno siano l'immediato successore di Aleph-zero?

Possiamo porre la domanda in un altro modo. Si potrà mai trovare un insieme infinito che abbia una potenza strettamente compresa fra gli insiemi dei Numeri Naturali e dei Numeri Reali? Ovvero, un insieme che non possa essere contato dai Numeri Reali, ma che non possa a sua volta "contare" il Continuo?

Cantor ha passato gli ultimi anni della sua vita a cercare di dimostrare questa che i matematici chiamano "ipotesi del Continuo", cioè che non esista nessun insieme infinito compreso fra quelli dei numeri naturali e dei numeri reali, ma senza riuscirci. E abbiamo già accennato come David Hilbert abbia incluso proprio questo teorema al primo posto fra i suoi "23 problemi" al Congresso di Parigi del 1900.

Il problema si è rivelato davvero difficile da aggredire, tant’è che solo nel 1940 Kurt Gödel (toh, chi si rivede!) ha dimostrato che non è dimostrabile la falsità dell’ipotesi del Continuo. Sembra un passo incoraggiante: se non è possibile che l'ipotesi sia falsa, allora dovrebbe essere vera...

... Invece nel 1963 Paul Cohen ha dimostrato che è impossibile dimostrare che l’ipotesi del Continuo sia vera! Ecco quindi saltar fuori un’antinomia, un enunciato che porta a conclusioni contraddittorie! Solo che, a differenza del paradosso di Russell, che rivelava un’antinomia in una cosa che sembra (almeno a noi comuni mortali) più una pignoleria che un problema reale, adesso l’antinomia salta fuori dallo studio dei numeri, cioè al livello più basilare di tutto ciò che è matematica.

L'unione dei risultati di Gödel e di Cohen diviene un esempio "pratico" di quelle proposizioni indecidibili che Gödel aveva precedentemente dimostrato esistere nel suo Secondo Teorema di Incompletezza. Per il suo risultato, Cohen ricevette nel 1966 la Medaglia Fields, ovvero la massima onorificenza per matematici di età inferiore ai quarant'anni.

A proposito delle dimostrazioni di Gödel e Cohen, ho chiesto lumi a un professore universitario mio amico che insegna proprio questo genere di cose. In sostanza la domanda era se tali dimostrazioni potessero essere comprese anche da uno come me, non del tutto digiuno di matematica, ma pur sempre un dilettante. La risposta è stata le seguente:

Le dimostrazioni di Gödel e Cohen sono difficili anche per me... Le idee le conosco, ma certi dettagli tecnici nemmeno io li afferro completamente. Certo, studiandoli per bene, penso che ce la farei!

L'idea di Gödel si puo' anche descrivere abbastanza facilmente, ma dimostrarla con tutti i crismi non è una passeggiata. L'idea della dimostrazione di Cohen invece si puo' dare solo vagamente e, per apprezzarla appieno, bisognerebbe entrare in dettagli sofisticati; dare poi la dimostrazione completa... non ne parliamo!

Ho deciso di lasciar perdere...

-------------------------

L'insieme di idee che i personaggi di cui ho parlato in queste pagine è riuscito a mettere insieme è una delle vette massime raggiunte dall'umanità. Non ha importanza se il risultato alla fine sia un apparente "nulla di fatto", con queste antinomie che saltano fuori da tutte le parti. Sono assolutamente d'accordo con Carl Jacobi, che scrisse:

"L'unico scopo della scienza è l'onore dello spirito umano; a questo titolo una questione sui numeri vale quanto una sul sistema del mondo"

La potenza dei procedimenti logici avviata da Cantor con il suo approccio agli insiemi infiniti si è rivelata davvero formidabile, anche se molti matematici suoi contemporanei non l’hanno subito apprezzata. In mezzo a dispute anche aspre su questo argomento, David Hilbert ebbe a dire:

"Nessuno ci scaccerà dal Paradiso che Cantor ci ha procurato!"   ▲  

Questioni... teologiche!

Voglio finire questa dissertazione con un paio di aneddoti che riguardano Galileo e Cantor alle prese con l'infinito, questo concetto non solo numerico, ma anche filosofico e, soprattutto, teologico.

Il concetto di infinito inizia ad essere sfruttato in teologia da Nicola Cusano (1401-1464) che confronta in varie occasioni l’infinità di Dio con la finitezza degli uomini, e l’intelletto (finito) con la Verità (infinita). A lungo andare quindi l’infinito ha condensato un sacco di attributi divini... diventando un termine da usare con le molle.

Come abbiamo visto Galileo Galilei si è imbattuto in alcuni ragionamenti logici che riguardano l’infinito; ma la sua mancanza di coraggio nell’arrivare alle loro estreme conseguenze forse è da ascrivere al timore di dare altri argomenti all’inquisizione... con cui aveva già i suoi bei problemi! Non va dimenticato che pochi anni prima, nel 1600, Giordano Bruno era stato condannato al rogo anche per aver detto "È dunque l'universo uno, infinito, immobile...", mentre secondo l’inquisizione (il cardinale Roberto Bellarmino, Dottore della Chiesa, è quello che condannò sia Giordano Bruno che Galileo) l’universo è finito e gira, mentre è la terra a stare immobile.

Anche Cantor si pose qualche problema al momento di divulgare le sue teorie sugli insiemi infiniti, soprattutto per quanto riguarda l’esistenza di infiniti di varia grandezza. Da buon cristiano si chiese se usare il termine infinito non avrebbe disturbato la gerarchia ecclesiastica; era la fine dell'ottocento, non c'era più pericolo di andare al rogo, però volle comunque sapere che cosa avrebbe pensato di questo fatto la gerarchia cattolica. Andò in Vaticano, portò i suoi lavori al Santo Uffizio, che era governato da un cardinale tedesco, a cui disse: "Eminenza io ho qui lavori di matematica che mi dicono che ci sono più infiniti, in realtà tanti infiniti". Il cardinale disse: "Insomma io la matematica non la conosco... mi lasci i suoi lavori, che li faccio studiare ai miei segretari".

I segretari erano dei domenicani, che si presero due anni, perché ovviamente hanno dovuto cominciare a studiare la teoria degli insiemi da zero. Dopo due anni dissero al cardinale: "Secondo noi non c'è problema, non c'è pericolo per la fede". Allora Cantor venne convocato in Vaticano e il cardinale del Santo Uffizio gli disse: "Guardi lei può parlare di questi infiniti, purché non li chiami infiniti, perché effettivamente questo darebbe una brutta idea teologica, cioè farebbe una connessione con la divinità". Allora Cantor scelse il nome "transfiniti"; ma, per ironia della sorte, i matematici preferiscono chiamarli con il nome di... numeri Cardinali!

Il cardinale del Santo Uffizio si era anche fatto l’idea che dopo tutti questi transfiniti, là, alla fine, ci fosse il vero infinito assoluto. Chiese a Cantor cosa ne pensasse: "Per noi matematici quello non c'è. Non esiste un infinito assoluto per i matematici, perché ciò sarebbe contraddittorio". Al che il cardinale rispose: "Va bene: quello lì è nostro!".   ▲  

Numeri Transfiniti: il contesto storico

Sommario:

+ I numeri Naturali
+ Ancora Aleph-zero
– Il contesto storico
      Rifondare la matematica
      Giuseppe Peano
      Bertrand Russell
      Gottlob Frege
      David Hilbert
      Kurt Gödel
+ Oltre Aleph-zero: il Continuo
+ L'ipotesi del Continuo

Rifondare la matematica

Nel XIX secolo la matematica era arrivata a un livello di sviluppo veramente notevole, ed era in continua evoluzione. Qualcuno cominciò ad avere dei dubbi sulla correttezza di tutto ciò, in quanto è bensì vero che da premesse valide, con ragionamenti corretti, si arriva sempre a conclusioni altrettanto valide; ma siamo sicuri che tutte le premesse siano valide, e che da qualche parte non sia stato commesso un qualche errore di ragionamento?

Si andavano profilando due ordini di dubbi, dei quali il primo era già stato indicato da Kant nella "Critica della ragion pura". Questo era: quanto può il processo di induzione essere portato avanti senza "partire per la tangente"? Il secondo ordine di dubbi invece era: le basi sulle quali si appoggia tutto il castello sono davvero solide?

L’Analisi Matematica era (ed è) un campo cruciale, in quanto consente di descrivere il funzionamento dei sistemi fisici. In questo campo si gioca abbastanza disinvoltamente con zeri, infiniti e infinitesimi, si fanno addirittura somme di infiniti infinitesimi. Per fortuna l’Analisi ha spesso il modo di confrontarsi con la fisica, per cui storicamente è capitato anche che non sia stata la fisica a essere "capita" dalla matematica, ma la matematica ad essere "convalidata" dalla fisica.

Certo questo modo di procedere non poteva bastare ai matematici, puntigliosi e perfezionisti come sono: ecco quindi la necessità di fare un ragionamento complessivo sulla materia, cercando di partire dal minor numero di assiomi, per poi arrivare alle questioni più complesse per piccoli passi, incontrovertibilmente dimostrabili. (Gli assiomi, anche detti postulati, sono enunciati che, pur non essendo dimostrati, sono considerati veri; vengono usati per fornire i punti di partenza necessari alla delineazione di un quadro teorico, come può essere quello della teoria degli insiemi).   ▲  

Giuseppe Peano



Dovendo iniziare dalle cose più semplici, la cosa ovvia era di partire dai numeri naturali. I quali, pur essendo intuitivi, richiedevano una definizione precisa. Giuseppe Peano (1858-1932), il primo logico matematico italiano della storia, li definì in base a questi cinque assiomi:

— Esiste un numero naturale zero
— Ogni numero naturale ha un numero naturale successore
— Numeri diversi hanno successori diversi
— Zero non è il successore di alcun numero naturale
— Ogni insieme di numeri naturali che contenga lo zero e il successore di ogni proprio elemento coincide con l'intero insieme dei numeri naturali

Io li trovo magnifici, ma non tutti la pensano così. Per esempio la definizione di "successore" non è stata considerata sufficientemente precisa, si potrebbe contare di due in due, o di tre in tre... (i logici, coloro che si occupano di logica, riescono ad essere addirittura più puntigliosi e precisi dei matematici!)

I logici sanno che devono stare molto attenti: non è detto che le loro costruzioni non entrino mai in contraddizione. Lo scoprirono già gli antichi greci, grazie a tale Epimenide di Creta (VI secolo a.C.), il quale, cretese appunto, ebbe a dire che "tutti i Cretesi sono bugiardi". Si capisce bene che si tratta di un paradosso: se egli, cretese, stesse dicendo la verità, allora non sarebbe vero che tutti i cretesi sono bugiardi; se invece fosse bugiardo, starebbe affermando una cosa vera! (*) Contraddizioni di questo tipo, o "antinomie" (le situazioni per cui, posta una questione particolare, se ne possono ricavare due affermazioni apparentemente valide ma che sono in contrasto fra loro) sono sempre in agguato.

(*) Il paradosso del mentitore, come espresso da Epimenide, non è corretto: basta pensare che almeno un cretese dica la verità. Allora Epimenide sarebbe effettivamente bugiardo dicendo che i cretesi sono tutti bugiardi, perché in realtà ce n'è uno che non lo è. Comunque i logici moderni hanno saputo creare altri paradossi per cui... non c'è scappatoia che tenga!   ▲  

Bertrand Russell



Insomma, i logici ci pensano un po’ su, trovano che i numeri naturali non sono la base giusta da cui partire, e cercano qualcosa di più potente e versatile: inventano il concetto di Insieme. In effetti si può verificare l'efficacia della Teoria degli Insiemi proprio nel definire la serie dei Numeri Naturali: come vedremo fra poco, si tratta di una costruzione davvero elementare (nel senso che richiede un numero veramente ridotto di concetti di base, anche se non è una cosa affatto semplice).

Gli insiemi sono collezioni di uno o più elementi distinguibili l’uno dall’altro (esiste anche l’insieme vuoto); il numero di elementi contenuto da ciascun insieme è detto potenza dell’insieme. L’insieme vuoto ha quindi potenza zero, quelli con un solo elemento hanno potenza uno, e così via. Per ottenere l'intera serie dei numeri naturali basta procedere come segue:

— all’insieme vuoto, che ha zero elementi e quindi ha potenza 0, viene associato il numero zero.

— si crea la regola per cui il successore B di un insieme A è dato dall’unione degli elementi dell’insieme A con l’insieme A stesso; in questo modo si aggiunge l’elemento costituito dall’insieme A agli elementi già contenuti in A, ottenendo un insieme B che ha una potenza maggiore di un'unità rispetto all'insieme A: assoceremo alla potenza di questo nuovo insieme il numero naturale corrispondente.

Vediamo meglio come funziona il tutto: agli elementi dell'insieme vuoto (che non ne ha) aggiungo l'insieme vuoto stesso, ottenendo l'insieme uno che conterrà solo un insieme vuoto, e quindi avrà potenza uno; agli elementi dell'insieme uno (che contiene un insieme vuoto) aggiungo l'insieme uno e ottengo l'insieme due (conterrà l'insieme vuoto e l'insieme uno); quello tre avrà tre elementi (l'insieme vuoto, l'uno e il due), e così via: ciascuno con potenza pari al numero di elementi che contiene. Avendo associato ciascuno di questi insiemi ai numeri che esprimono la loro potenza, con questo abbiamo definito l'intera serie dei numeri naturali.

In sostanza, bastano i concetti di insieme (e insieme vuoto) e di successore per creare l'intera serie dei Numeri Naturali!

Fra il XIX e il XX secolo gli studi per rifondare la matematica andarono avanti speditamente, con e senza l'uso della teoria degli insiemi (non tutti i matematici la vedevano di buon occhio; ma come abbiamo visto, e vedremo ancora, Georg Cantor la usò in modo spettacolare per aggredire il concetto di infinito). Le basi a quel punto erano davvero solide, e c'era la convinzione diffusa che non si sarebbe mai trovata una contraddizione, non si sarebbe mai trovato un paradosso (o antinomia, come quella del mentitore).   ▲  

Gottlob Frege



Anche Gottlob Frege (1848-1925), considerato uno dei più grandi logici dopo Aristotele, stava contribuendo alla ricostruzione della matematica. Aveva già pubblicato il primo tomo del suo "Principi di Aritmetica" e stava per andare in stampa con il secondo volume, quando riceve una lettera da Bertrand Russell. Russell affronta la seguente questione:

Può un insieme essere elemento di sé stesso, ovvero contenere se stesso?

La risposta è sì. Ad esempio, l'insieme di tutti i libri di una biblioteca non è elemento di sé stesso. Invece, l'insieme di tutti gli insiemi con più di 20 elementi è elemento di sé stesso. Allora vediamo quest’altra questione:

Che tipo di insieme salta fuori se ne creo uno che contenga tutti gli insiemi che non contengono se stessi?

Vediamo per tentativi, provando a considerare o meno questo insieme come elemento di se stesso:

— se dico che questo insieme non contiene se stesso, fa parte del gruppo degli insiemi che non contengono se stessi, e quindi dovrebbe farne parte (ma l'ipotesi era che non ne facesse parte)

— se dico che questo insieme contiene se stesso, non fa parte del gruppo degli insiemi che non contengono se stessi, e quindi non dovrebbe farne parte (ma l'ipotesi era che ne facesse parte)

Ecco il paradosso fatale: alla creazione dell'insieme degli insiemi che non contengono se stessi consegue la comparsa di un'antinomia, ed è quanto basta per smontare l’illusione di un sistema logico completo e coerente. L’esistenza di una contraddizione come questa è la crepa che fa crollare il castello.

Frege prese atto delle conseguenze distruttive per il sistema che aveva costruito e si rassegnò a scrivere un'appendice ai suoi Principi, in cui confessava il fallimento della sua opera. Le contraddizioni messe in luce dal paradosso di Russell sono insolubili nell'ambito della teoria degli insiemi, e i logici matematici hanno dovuto sudare parecchio per imparare a gestire questo stato di cose.   ▲  

David Hilbert



... e la Geometria? Nel XIX secolo erano stati compiuti moti sforzi per "assiomatizzare", ovvero riformulare su basi logiche, un po' tutti i campi della matematica. Ma la Geometria, che peraltro aveva avuto sviluppi grandiosi (ad esempio con la nascita delle Geometrie non Euclidee), era stata per lo più esclusa da questo processo.

La lacuna viene colmata da David Hilbert (1862-1943) il quale, nel 1899, pubblica un testo fondamentale: i Fondamenti della Geometria (di cui accenno qui qualche dettaglio). Si tratta del primo risultato veramente compiuto di assiomatizzare una parte della matematica senza incorrere in antinomie o contraddizioni. Il testo ebbe successo immediato, spronando ancor di più gli sforzi per arrivare a risultati analoghi negli altri campi della matematica — peraltro potremmo dire che con questo testo Hilbert spronava anche sé stesso, anche se era conscio del fatto che il compito sarebbe stato superiore alle proprie forze (come a quelle di qualsiasi altro singolo matematico), quindi approfittò di una circostanza molto particolare:

Nel 1900 a Parigi si riuniva il secondo Congresso Internazionale dei Matematici (il primo si era svolto a Zurigo nel 1893). Invitato a intervenire, Hilbert, invece di illustrare qualche proprio risultato già raggiunto, espose un elenco di problemi da risolvere: era una specie di "compito in classe" per tutto il mondo matematico del secolo a venire.

Nel suo intervento Hilbert elenca una decina di problemi, scelti fra la lista di quelli che saranno poi conosciuti come i ventitré "Problemi di Hilbert" (l'elenco completo compare nella memoria scritta da Hilbert per la pubblicazione negli atti del congresso). Di questi, alcuni furono risolti in breve tempo, altri hanno richiesto vari decenni, mentre qualcosa è stato incluso anche fra i sette "Problemi per il Millennio", un elenco analogo a quello di Hilbert, promosso dall'Istituto Matematico Clay nel "Convegno del Millennio" di Parigi, il 24 maggio 2000.

Dei problemi di Hilbert, per l'argomento che stiamo trattando in questi capitoli sono di particolare interesse i primi due:

1 — Dimostrare l'ipotesi del Continuo;
2 — Dimostrare la validità assoluta degli assiomi dell'aritmetica.

Del primo problema ci occuperemo nei prossimi capitoli, mentre il secondo problema chiede di fare proprio ciò di cui ci stiamo occupando qui: dimostrare (come era già stato fatto per la geometria euclidea, proprio a opera di Hilbert) che gli assiomi dell'aritmetica sono anch'essi consistenti e coerenti. Vediamo cosa significano esattamente questi due termini:

Consistenza — Gli assiomi alla base di una teoria (in questo caso, l'aritmetica) devono essere completi (o sufficienti), in modo da coprire tutti i possibili sviluppi della teoria; inoltre bisogna verificare che non verranno mai in conflitto fra loro, ovvero che non ne possano nascere contraddizioni.

Coerenza — Garantire che i teoremi che saranno sviluppati a partire dallo stesso insieme di assiomi non saranno mai in contraddizione fra loro.

(Tutto sommato, sembra il minimo che si possa chiedere a una teoria matematica...)

Nell'introduzione al suo discorso, Hilbert fa riferimento a due problemi matematici antichissimi: la quadratura del cerchio e la duplicazione del cubo. A seguito di secoli e secoli di tentativi andati a vuoto, finalmente nel XIX secolo si è dimostrata l'impossibilità di risolverli. E questo tutto sommato è un fatto positivo: è sicuramente meglio che un'affermazione sia dimostrata falsa piuttosto che rimanere nel dubbio, o peggio, arrivare a dimostrarne la "indecidibilità".

Purtroppo nei tentativi di assiomatizzare la matematica i casi indecidibili stavano continuando ad emergere, come l'Antinomia di Russell già citata; ecco quindi il compito assegnato ai matematici: cercare di eliminare questo genere di anomalie.   ▲  

Kurt Gödel



La speranza di costruire un castello interamente coerente della matematica si è infranta definitivamente nel 1931, quando Kurt Gödel (1906-1978) dimostrò il suo Primo Teorema di Incompletezza. Questo dice:

In ogni teoria matematica T ... esiste una formula F tale che, se T è coerente, allora né F né la sua negazione sono dimostrabili in T.

Questo teorema (semplificando) afferma che in un sistema assiomatico salterà sempre fuori un enunciato non dimostrabile a partire dagli assiomi di partenza, ovvero un caso indecidibile del quale non si può dire se sia vero oppure falso.

Il Secondo Teorema di Incompletezza recita invece:

Nessun sistema coerente può essere utilizzato per dimostrare la sua stessa coerenza.

In pratica, se voglio costruire un sistema matematico partendo da qualche assioma di partenza, avrò bisogno di qualche assioma esterno alla teoria per verificarne la validità...

Questi risultati di Gödel vengono da qualcuno considerati il risultato più decisivo raggiunto nel campo della logica matematica: infatti sembra precludere ogni speranza di arrivare a una certezza matematica. Per fortuna, i matematici non si sono sentiti tarpare le ali da questi teoremi, tant'è che hanno continuato, e continuano, a produrre teoremi su teoremi...

Insomma, stiamo attenti a dire che la matematica è "tutta sbagliata": rischieremmo di buttare via il bambino con l'acqua sporca! Si è solo scoperto che la coerenza logica, quando si raggiungono certi ragionamenti limite, non è pienamente raggiungibile. Ma quando pagate il conto al ristorante, state tranquilli che nel calcolo del resto non si presenterà mai alcuna antinomia!   ▲  

Prossimo capitolo: Il Continuo

Numeri Transfiniti: Aleph-zero

Sommario:

+ I numeri Naturali
– Ancora Aleph-zero
      Numeri Razionali
      Numeri Irrazionali
      Numeri Algebrici
      Numeri Negativi
      Irrazionalità di √2
      Irrazionalità delle radici non intere
+ Il contesto storico
+ Oltre Aleph-zero: il Continuo
+ L'ipotesi del Continuo

Ancora Aleph-zero

Nel primo capitolo di questa "scorribanda" fra gli insiemi infiniti abbiamo scoperto che non si trovano, diciamo così, insiemi infiniti "piccoli". Detto in termini più precisi: non esistono insiemi infiniti di cardinalità, o potenza, minore dell’insieme dei numeri naturali; la cui cardinalità si identifica con la sigla Aleph-0. Ora vogliamo vedere se riusciamo a trovare insiemi infiniti più grandi di Aleph-0.

Per trovare un insieme "più grande" di quello dei numeri naturali bisogna (tenetevi forte!) trovare "un insieme che abbia una funzione iniettiva rispetto all'insieme dei numeri naturali, ma nessuna corrispondenza biunivoca con esso"! Detto in altre parole: occorre scovare un insieme infinito che contenga alcuni membri (in teoria ne basta anche uno solo), che non possa essere messo in corrispondenza con un qualche elemento dell'insieme dei numeri naturali. Si può dire altresì che gli elementi dell'insieme più grande non potranno essere "contati": solo verificando questa condizione saremo sicuri di aver trovato un insieme di cardinalità maggiore di Aleph-0.   ▲  

Numeri Razionali

Possiamo fare un primo tentativo prendendo in esame i numeri razionali, che sono quelli che si ottengono dal rapporto tra due numeri naturali (il termine "razionale" deriva dal latino "ratio", proprio nel suo significato di rapporto). Ogni numero razionale è il risultato di una divisione a/b in cui a è il numeratore e b il denominatore; b deve ovviamente essere diverso da zero, mentre se abbiamo b=1 il risultato è un numero intero: i numeri interi (naturali) sono quindi un sottoinsieme dei numeri razionali.

Nell’intervallo compreso fra ogni coppia di numeri interi consecutivi posso inserire quanti numeri razionali voglio; qui sotto vi mostro una rappresentazione grafica di questo concetto:



fra i numeri 1 e 2 ho inserito 3/2 (1,5), 4/3 (1,333...), 9/5 (1,8), ovviamente ci sono infinite altre possibilità (ne ho indicate qualcuna con quei punti interrogativi). Calcolando il quoziente fra numeratore e denominatore di ciascuna di queste frazioni si ottiene un numero decimale con un numero finito o addirittura infinito di cifre dopo la virgola (in quest'ultimo caso, come abbiamo imparato alle medie, i decimali saranno periodici).

Ecco, mi vengono in mente almeno tre motivi per cui i numeri razionali dovrebbero essere in quantità maggiore rispetto ai numeri naturali: il fatto che fra ogni coppia di numeri naturali consecutivi posso inserire infinite frazioni; la presenza di tutti quegli infiniti decimali; infine il fatto che ogni numero razionale viene definito da due numeri naturali (numeratore e denominatore). E invece...

#1


Ecco, in questa griglia ho inserito tutte le frazioni possibili e immaginabili: basta cercare il numeratore sull’asse delle X (orizzontale) e il denominatore sull’asse delle Y (verticale); ovviamente lo schema può essere ingrandito a piacimento. Ho inserito anche dei pallini colorati e numerati: il numero 1 accanto alla frazione 1/1, poi 2 per 2/1 e 3 per 1/2, poi ancora 4 per 3/1, 5 per 2/2 e 6 per 1/3, e così via. In questo modo sto "contando" per diagonali successive tutte le frazioni possibili, anche quelle non ridotte ai minimi termini.

Eccoci quindi al punto: siccome i numeri naturali sono in grado di "contare" le frazioni, e quindi i numeri razionali (*), vuol dire che i due insiemi (dei numeri naturali e dei numeri razionali) possono essere messi in corrispondenza biunivoca, quindi hanno la stessa potenza: sempre Aleph-0.

(*) Precisazione: alcune frazioni che compaiono nella griglia #1 danno luogo allo stesso numero naturale (es. 1/1 e 2/2 = 1) o razionale (es. 1/2 e 2/4 = 0,5); per avere numeri razionali tutti diversi l'uno dall'altro dovrei escludere dal conteggio tutte le frazioni non ridotte ai minimi termini.

Escludere le frazioni non ridotte ai minimi termini è una cosa che si può fare, anche se non è facilissima quando numeratore e denominatore diventano molto grandi. Però si tratterebbe di una fatica inutile:

— l'insieme dei numeri naturali è un sottoinsieme dell'insieme dei numeri razionali (che comprende tutti i numeri naturali)

— l'insieme dei numeri razionali è un sottoinsieme dell'insieme delle frazioni, in quanto più frazioni danno luogo allo stesso numero razionale

— nella griglia #1 ho mostrato la corrispondenza biunivoca fra gli insiemi dei numeri naturali e delle frazioni, che sono quindi equipotenti e di cardinalità Aleph-0.

— allora anche l'insieme dei numeri razionali, che è apparentemente "compreso", come potenza, fra gli altri due, non può che avere potenza Aleph-0 (ometto la dimostrazione rigorosa).   ▲  

Numeri Irrazionali

Facciamo un altro tentativo: proviamo con i numeri irrazionali, come la radice quadrata di due. Questo numero ha una lunga storia: per il teorema di Pitagora la radice quadrata di due coincide con la lunghezza della diagonale di un quadrato di lato unitario:



Pitagora era un entusiasta sostenitore della "comprensibilità" dell’universo, nel senso che cercava di "misurarne" i segreti in termini di rapporti. Per esempio aveva studiato le note musicali scoprendo che hanno fra loro delle relazioni "razionali"; aveva anche immaginato il sistema delle "sfere celesti" come supporto per i pianeti e le stelle fisse, sfere sempre in rapporto razionale fra loro; e mescolando le note musicali con le sfere celesti aveva immaginato quella che ancora oggi chiamiamo "armonia delle sfere".

Insomma Pitagora era felicissimo di avere trovato... proprio il teorema di Pitagora! Però ci rimase molto male quando scoprì che la radice quadrata di due non è un numero razionale. Mettetevi nei suoi panni: vuole capire l’universo mondo, scopre un teorema straordinario che lo può aiutare a capirlo meglio, e il primo risultato che trova sfugge al suo criterio su cosa è razionale e cosa non lo è (per la dimostrazione della non razionalità del numero radice di due, vedi sotto). In altre parole: riesce a dimostrare che la radice di due non può essere definita da nessuna frazione a/b, in cui a e b siano numeri interi.

In epoca più moderna è stato dimostrato un teorema molto più generale (vedi ancora sotto), che dice che ogni radice di qualsiasi grado, di qualsiasi numero naturale, può dare come risultato o un numero intero o un numero irrazionale; numeri razionali, mai.

Insomma stiamo scoprendo una quantità enorme di numeri che non sono razionali. Il fatto di non esserlo, vuol dire che la loro rappresentazione decimale non presenterà nessun carattere di periodicità, avendo sequenze infinite di cifre decimali in successione, diciamo così, caotica. Questa cosa trova una facile spiegazione: se ricordate la matematica delle medie, ci avevano insegnato a trovare la "frazione generatrice" dato un qualunque numero decimale periodico, con o senza antiperiodo. Quindi se i numeri irrazionali, come la radice di due, fossero numeri decimali periodici, avrebbero la loro bella frazione generatrice... e allora sarebbero razionali e non più irrazionali.

Questi numeri irrazionali sono degli ottimi candidati per vedere se possono dar luogo a un insieme infinito più grande, ovvero di cardinalità più grande, rispetto all’insieme dei numeri naturali. Ma come ormai vi aspetterete... non è così! Infatti posso usare lo stesso "trucco" usato per i numeri razionali: invece di mettere nel grafico tutte le frazioni possibili, metto tutte le radici possibili. Quindi avrò la riga delle "radici prime" (di fatto, la riga dei numeri naturali); poi la riga delle radici quadrate, delle radici cubiche, poi delle radici quarte, quinte eccetera. E tutte queste radici le potrò numerare per diagonali, come avevo fatto con le frazioni: quindi neanche in questo caso ho ottenuto il mio scopo!

#2


Per le radici di numeri che danno luogo a numeri interi, come radice quadrata di 4 o radice cubica di 27, vale lo stesso discorso fatto qui sopra per i numeri razionali.   ▲  

Numeri Algebrici

C’è un piccolo problema: il nuovo "conteggio" visto sopra lascia fuori i numeri razionali, per esempio la frazione 2/3 non è compresa. Come fare per mettere insieme le due classi di numeri? Beh, basta fare un doppio conteggio. Nella tabella #1 avevamo contato i numeri razionali: se sostituiamo i numeri sotto radice nella tabella #2 con le loro frazioni corrispondenti, otterremo una tabella in cui compaiono tutte le radici (radici di ogni grado) di tutti i numeri i razionali; quindi:

— le radici di primo grado delle frazioni con l’unità al denominatore danno luogo ai numeri naturali;

— le radici di primo grado dei numeri razionali danno luogo ai razionali stessi;

— tutte le radici di secondo, terzo grado e oltre, danno luogo a tutte le radici possibili, dei numeri naturali come dei numeri razionali.

#3


Possiamo immaginare a questo punto di complicare le cose quante volte si vuole: troveremo sempre il modo di "contare" espressioni algebriche sempre più complicate, senza mai trovare un insieme infinito di cardinalità superiore ad Aleph-0!

Nella griglia #3 sto mettendo in corrispondenza i numeri naturali con espressioni del tipo radice ennesima di a/b. Anche qui, molte espressioni possono dar luogo allo stesso numero, intero, razionale o irrazionale che sia; vale comunque lo stesso ragionamento già fatto qui sopra.   ▲  

Numeri Negativi

Ma ora che mi viene in mente, come la mettiamo con lo zero e i numeri negativi? A questo punto è semplice: basta fare una conversione di questo tipo:

1  —    0
2  —    1
3  —  –1
4  —    2
5  —  –2
6  —    3
7  —  –3
...

In sostanza sto mettendo in corrispondenza biunivoca la serie dei numeri naturali (numeri di sinistra) con lo zero e i numeri interi di entrambi i segni (a destra). Naturalmente possiamo sostituire a ogni numero di destra (senza segno) la rispettiva frazione, o radice, o radice di frazione, o qualsiasi altra espressione algebrica che vogliamo!

Da ciò che abbiamo visto in questa e nel capitolo scorso, gli insiemi dei numeri naturali; gli insiemi apparentemente "più piccoli" come i soli numeri pari, o i quadrati, o i numeri fattoriali; e gli insiemi apparentemente "più grandi" come i numeri razionali, irrazionali, e algebrici, anche considerando il segno... tutti questi insiemi sono equipotenti, e hanno cardinalità Aleph-0!   ▲  

Irrazionalità di √2

Questa dimostrazione compare negli "Elementi" di Euclide, ed è basata su un ragionamento per assurdo.

Sia [AB] il lato e [AC] la diagonale di un quadrato, e si supponga che i due segmenti stiano tra loro come la frazione m/n, ridotta ai minimi termini. Allora:

[AC]² : [AB]² = m² : n²

Ma, per il teorema di Pitagora:

[AC]² = 2 ּ [AB]²

E quindi:

m² = 2 ּ n²

Ne consegue che m², e perciò m, è pari. Deve dunque essere dispari il numero n. Poniamo allora

m = 2 ּ q

Allora

m² = 4 ּ q² = 2 ּ n²
2 ּ q² = n²

Di conseguenza n² è pari. È quindi pari anche n, che si è dimostrato dover essere dispari. Ne nasce un’incompatibilità che prova l’asserto.   ▲  

Irrazionalità delle radici non intere

"Siano a ed n due numeri naturali. Se la radice a-ma di n non esiste nel campo nei numeri interi, essa non esiste neppure nel campo dei numeri razionali."

Lo si dimostra per assurdo. Sia x = p / q un numero razionale tale che xª = n, con p e q primi tra loro. Allora anche pª e qª sono primi tra loro.

Dovendo essere n = xª = (p / q)ª, risulta pª = n ּ qª e perciò qª è un divisore di pª. Ma pª e qª sono primi tra loro, e ciò può avvenire soltanto se qª = 1. Sarebbe allora x = p / 1, un numero intero, contrariamente all'ipotesi.   ▲  

Prossimo capitolo: Il contesto storico

I Numeri Transfiniti

Comincia qui una spiegazione che inizia con qualche considerazione sui numeri naturali, la loro "quantità" e la ricerca di vari tipi di insiemi infiniti. Il tutto con il racconto dei personaggi, delle conquiste e, purtroppo, dei clamorosi fallimenti: è un racconto a tratti davvero avvincente.

Sommario:

– I numeri Naturali
      Insiemi e "corrispondenza biunivoca"
      Numeri infiniti
      Aleph-zero
      Infiniti "più piccoli"?
      Numeri Transfiniti
      Intermezzo: l'albergo con infinite stanze
+ Ancora Aleph-zero
+ Il contesto storico
+ Oltre Aleph-zero: il Continuo
+ L'ipotesi del Continuo

Insiemi e "Corrispondenza Biunivoca"

La teoria degli insiemi non mi è stata insegnata a scuola: solo quando è diventata "di moda" ho cominciato a chiedermi a cosa servisse. Tutte quelle infinite definizioni come "unioni", "intersezioni", funzioni "iniettive" e "suriettive"... mi sembravano solo un modo di vessare i poveri studenti. Insomma non ne ho vista l’utilità pratica fino a quando non mi sono imbattuto nello studio dell’infinito, per il quale studio in realtà sono sufficienti due soli concetti: quello di insieme, appunto, e quello di "corrispondenza biunivoca".

Un insieme è una collezione di oggetti di vario genere, tutti diversi (o almeno, distinguibili) l’uno dall’altro. Per fare un esempio, posso considerare che la mia mano sinistra sia l’insieme delle sue cinque dita, e la mano destra l’insieme di altre cinque dita.

Domanda: come posso fare per stabilire se questi due insiemi (le mani) contengono lo stesso numero di elementi (dita)? Posso contarli:



Oppure posso mettere in correlazione ciascun dito della mano sinistra con il rispettivo dito della mano destra:



In quest’ultimo caso ho messo in atto il concetto di "corrispondenza biunivoca": ad ogni elemento (dito) del primo insieme (mano sinistra) corrisponde uno ed un solo elemento (dito) del secondo insieme (mano destra), e viceversa. Avendo unito le dita delle due mani come si vede nella foto, posso affermare senza ombra di dubbio che la "potenza", o "cardinalità", o più semplicemente il numero di elementi contenuto da ciascuno dei due insiemi, è lo stesso. Non occorre contarli, non occorre affatto sapere quanti sono; la domanda era: hanno i due insiemi lo stesso numero di elementi? La risposta è senz’altro: Sì.

Se invece alla mano sinistra mancassero due dita:



la corrispondenza biunivoca non ci sarebbe più. Le dita della mano sinistra troverebbero la loro corrispondenza nelle rispettive dita della mano destra, ma qualche dito della mano destra non lo troverebbe più nella mano sinistra: ecco quindi che, anche non sapendo quante dita (elementi) contiene ciascuna mano (insieme), posso affermare che la mano destra ha una "potenza", o "cardinalità", o un numero di elementi, superiore alla mano sinistra.

Tutto quanto detto finora è intuitivo, direi quasi banale, perché ci siamo occupati di insiemi non solo finiti, ma di insiemi di cui è facile contare il numero di elementi. Facciamo invece un esempio con insiemi più grandi (ma sempre finiti). Ammettiamo di radunare in un una piazza una quantità molto grande di persone, e di voler stabilire se ci sono più maschi o più femmine. Siccome le persone sono tante...



... mi è impossibile contarle senza commettere errori, tanto più se, come è probabile, non se ne staranno ferme. Allora posso chiedere loro di mettersi a coppie: ciascun maschio dovrà trovare una femmina con cui tenersi per mano. A questo punto basta vedere se "avanzano" maschi (che quindi risulterebbero essere in maggior numero delle femmine) o femmine (sarebbero in numero maggiore dei maschi); se non ci sono avanzi, vuol dire che il numero dei due gruppi è esattamente lo stesso. Di nuovo: non so quanti sono gli elementi di ciascun insieme (maschi / femmine) ma ho stabilito quale insieme è il più grande, o se hanno la stessa potenza e sono quindi equipotenti.   ▲  

Numeri Infiniti

Parliamo ora di numeri. Impariamo a contare dalla più tenera età, e scopriamo che esiste sempre un numero "più grande". Quando riusciamo a contare fino a cento, scopriamo subito che c’è anche il centouno. Fino al mille, e c’è il milleuno! Intuiamo presto che non ci sarà mai fine: magari non sapremo "come si chiama", ma ci sarà sempre un numero più grande di qualunque numero riusciamo ad immaginare. Ecco, abbiamo trovato il più classico esempio di "insieme infinito": l’insieme dei numeri naturali.

E qual è la cardinalità dell’insieme infinito dei numeri naturali? Non posso certo dire quanti numeri contiene, perché sono infiniti; e dire che questa cardinalità è infinito non sarebbe di nessuna utilità, in quanto "infinito" non è un numero.   ▲  

Aleph-zero

Per risolvere questo problema Georg Cantor (1845 – 1918), il padre della teoria degli insiemi, ha deciso di identificare la cardinalità dell’insieme dei numeri naturali con un simbolo costituito dalla prima lettera dell’alfabeto ebraico, Aleph, e dall’indice 0:



A differenza del nome "infinito", il valore Aleph-zero assume piena dignità di numero, tant’è che su questo e altri numeri del genere si possono fare particolari calcoli aritmetici.   ▲  

Infiniti "più piccoli"?

Tornando ai nostri numeri naturali, possiamo adesso inventarci un altro insieme infinito, quello che contiene i soli numeri pari. Apparentemente un insieme in cui mancano tutti i numeri dispari dovrebbe avere una potenza minore rispetto all’insieme di tutti i numeri naturali. Ma sarà vero?

Essendo infiniti, è ovvio che non posso "contare" gli elementi di ciascuno di questi insiemi. Però posso ricorrere al concetto di corrispondenza biunivoca; e grazie a questo stratagemma stabilire se veramente l’insieme dei soli numeri pari sia più piccolo dell’altro, più o meno come avevo fatto con le mie mani di tre e cinque dita.

Allora scrivo su due colonne i numeri dei due insiemi: a sinistra i numeri naturali, a destra i numeri pari; su ogni riga compare quindi un numero (a sinistra) e il suo doppio (a destra), e il trattino sta a rappresentare la corrispondenza fra gli elementi di ciascun insieme:

1 — 2
2 — 4
3 — 6
4 — 8
........

Evidentemente ciascuno dei numeri naturali dell’insieme di sinistra trova il suo corrispondente nel suo doppio nell’insieme di destra; e ciascun numero pari dell’insieme di destra trova il suo corrispondente nel numero metà dell’insieme di sinistra. Fra i due insiemi c’è uno stato di corrispondenza biunivoca, quindi hanno la stessa potenza!

Posso ripetere lo stesso procedimento con i numeri quadrati, mettendo in corrispondenza i numeri naturali con i loro quadrati:

1 — 1² = 1 x 1 = 1
2 — 2² = 2 x 2 = 4
3 — 3² = 3 x 3 = 9
4 — 4² = 4 x 4 = 16
........

I numeri quadrati sono ancora più "radi" dei numeri pari... eppure anche il loro insieme ha la stessa potenza dei numeri naturali. Proprio in questo ragionamento si imbatté Galileo Galilei, che nel "Dialogo sopra i due massimi sistemi del mondo" dice: "nel numero infinito, se concepir lo potessimo, bisognerebbe dire, tanti essere i quadrati tanti i numeri insieme". In pratica intuisce il principio per cui un insieme infinito ha la stessa potenza di una sua parte, dicendo che "i quadrati non sono in numero inferiore degli interi"; ma non si spinge a dire che siano proprio in numero uguale: infatti conclude "gli attributi di eguale maggiore e minore non hanno luogo ne gl’infiniti, ma solo nelle quantità terminate".

Voglio ora fare un altro esempio, che metto solo per cercare di spiegare quanto può essere grande... un numero grande! Creiamo un altro insieme di numeri, non pari, non quadrati, ma neanche cubi o di altre potenze: creiamo l’insieme dei numeri cosiddetti fattoriali. I quali sono il prodotto di tutti i numeri interi compresi fra 1 e il numero dato (i numeri fattoriali si indicano con il punto esclamativo):

1 — 1! = 1
2 — 2! = 1 x 2 = 2
3 — 3! = 1 x 2 x 3 = 6
4 — 4! = 1 x 2 x 3 x 4 = 24

I numeri salgono molto velocemente. Facciamo qualche altro esempio:

5 — 5! = 1 x 2 x 3 x 4 x 5 = 120
6 — 6! = 1 x 2 x 3 x 4 x 5 x 6 = 720
......
59 — 59! = 1 x 2 x 3 x 4 x ... x 58 x 59 = circa 1 seguito da 80 zeri.

Ecco, quest’ultimo numero, un 1 seguito da 80 zeri... è circa pari al numero totale di atomi che compongono l’intero universo. Cioè stiamo mettendo in corrispondenza il numero 59, un numero semplice, di uso direi quotidiano, con uno dei massimi numeri che abbiano un qualche significato fisico in natura! E andando avanti con numeri maggiori, otteniamo risultati praticamente impossibili da scrivere... riuscite a immaginarli?

   60 —     60!  = circa 8 seguito da 81 zeri, 80 volte il numero di atomi dell’universo
   61 —     61!  = circa 5 seguito da 83 zeri, 5000 volte il numero di atomi dell’universo
  100 —   100!  = circa 9 seguito da 157 zeri
1000 — 1000!  = circa 4 seguito da 2567 zeri
....

Insomma vengono numeri che non hanno più niente di confrontabile con qualsiasi cosa di reale. Notare che nell’insieme di sinistra siamo arrivati solo al mille; ma se mettessimo un miliardo, questo numero troverebbe tranquillamente il suo corrispondente nell’insieme dei numeri fattoriali... anche se non so neanche immaginare quante cifre possa avere il fattoriale di un miliardo!

Nonostante questo, gli insiemi dei numeri naturali e dei numeri fattoriali sono indubbiamente equipotenti e hanno quindi la stessa cardinalità.   ▲  

Numeri Transfiniti

Con questi discorsi abbiamo intuito che non è possibile trovare un sottoinsieme dei numeri naturali che sia infinito ma che abbia potenza minore dei numeri naturali stessi. In pratica l’insieme dei numeri naturali è il più piccolo insieme infinito esistente, la cui cardinalità, come dicevamo è identificata dal simbolo Aleph-0. Aleph-0 è il primo dei numeri cosiddetti "transfiniti". Procederemo nel prossimo capitolo alla (per il momento) vana ricerca di quelli successivi, relativi a infiniti "più grandi"... ma adesso facciamo un intermezzo!

Intermezzo: l'albergo con infinite stanze



L'altro giorno sono entrato in quest'albergo che vantava di avere... infinite stanze. Quando mi hanno detto che erano tutte occupate, ho chiesto se non si potesse fare qualcosa: il portiere ci ha pensato su, e poi ha chiesto a tutti gli ospiti dell'albergo di spostarsi nella stanza di numero uguale a quella che stavano occupando più uno. Così l'ospite della stanza numero uno è andato nella due, quello della due nella tre e così via: come per incanto è rimasta libera la stanza numero uno, che ho occupato felicemente non senza aver prima elargito un'adeguata mancia al portiere.

Il giorno dopo è arrivato un pullman con 1000 turisti, ma l'albergo era sempre pieno: il portiere ha ripetuto il giochetto, chiedendo a tutti gli ospiti di spostarsi nella stanza di numero uguale a quella già occupata più mille. Mi sono ritrovato nella stanza 1001.

Il giorno dopo ancora è arrivato un altro pullman, questa volta con infiniti turisti a bordo. Impossibile trovare alloggio per tutti? Macché: a ogni ospite dell'albergo è stato chiesto di spostarsi nella stanza di numero uguale al doppio di quella occupata. Si sono così liberate tutte le stanze dispari, in cui hanno trovato posto i nuovi arrivati; per quanto riguarda me, mi sono ritrovato nella stanza 2002 (in quest'albergo non si sta mai tranquilli!).

Il giorno dopo ancora, gli infiniti ospiti del pullman del giorno prima se ne sono andati. A questo punto il portiere (che ho scoperto essere anche il proprietario dell'albergo) si è messo a imprecare, e diceva: "come si fa a mandare avanti un albergo come questo, se metà delle stanze sono vuote?"

Gli ho suggerito io la soluzione: basta che ciascun ospite torni nella stanza metà di quella che occupava (in pratica tornando alla situazione precedente all'arrivo degli infiniti turisti). Paradossi dell'infinito...

Per questa storiella mi sono ispirato al racconto "L'hotel straordinario, o il milleunesimo viaggio di Ion il Tranquillo" di Stanislaw Lem, pubblicato nel libro "Racconti matematici" edito da Einaudi. [Lem è anche l'autore del romanzo di fantascienza "Solaris", dai cui è stato tratto l'omonimo film del 1972].

Prossimo capitolo: Ancora Aleph-zero

Spigolature

Una serie di curiosità e argomenti brevi, a cominciare da uno dei problemi più classici della geometria!

Sommario:
– Compito in classe
      Soluzione
+ La collana di Democrito

Compito in classe



Soluzione:



Non era difficile! :-)   ▲  

Spigolature: La collana di Democrito

Sommario:
+ Compito in classe
– La collana di Democrito
      Una pagliuzza d'oro...
      ... ne farò una collana!
      Quanto sarà lunga?
      Soluzione

Una pagliuzza d'oro...

L'altro giorno passeggiavo lungo il fiume, quando ho visto luccicare qualcosa: era una pagliuzza che sembrava d'oro. L'ho raccolta e, dopo averla fatta esaminare dal mio orafo di fiducia, ho scoperto che si trattava proprio di oro puro, e che aveva un volume pari a esattamente un millimetro cubo. Era una frazione di grammo (circa un cinquantesimo), quindi aveva un valore irrisorio; ma mi sono messo a fantasticare su cosa ne avrei potuto fare.   ▲  

... ne farò una collana!

Ho pensato a una collana per mia moglie, magari sottilissima. Lavorandoci un po' avrei potuto ottenere un filo tanto più lungo quanto più sottile, e pensavo che in teoria avrei potuto realizzare un filo infinitamente lungo anche se infinitamente sottile: la collana invisibile, però pur sempre una collana!

Però poi mi è venuto in mente Democrito, il quale è stato il primo a sostenere che la materia è fatta di atomi: parti piccolissime che non si possono più dividere. Allora la mia collana non avrebbe potuto essere infinitamente sottile, ma avrebbe dovuto fermarsi a uno spessore minimo pari al diametro di un atomo. Allora la domanda: quando sarebbe stata lunga la mia collana, se fossi riuscito a mettere in una singola fila tutti gli atomi di quella pagliuzza d'oro?

Pensavo di procedere così: dividendo il mio millimetro cubo in otto parti (due fette alte metà, ciascuna divisa in quattro quadretti - più o meno come si fa con le patate) avrei ottenuto una collana di spessore 0,5mm e lunga 4 mm (8 cubetti da 0,5mm ciascuno). Ripetendo l'operazione avrei ottenuto 64 cubetti da 0,25mm, per una lunghezza di 16mm; poi 64mm, 256mm, 1024mm (che sono già più di un metro)... fino ad arrivare a una collana in cui ciascun cubetto avrebbe contenuto un singolo atomo d'oro.   ▲  



Quanto sarà lunga?

Ho fatto un po' di calcoli e sono arrivato a determinare la lunghezza teorica della mia collana. Per ora vi propongo tre alternative, provate a rispondere: quanto può essere lunga, al massimo, una collana fatta a partire da un millimetro cubo d'oro?   ▲  

A - 15 chilometri
B - 15000 chilometri
C - 15 milioni di chilometri

Soluzione

Per chi fosse curioso su come ho fatto i calcoli, li inserisco qui. Chi è interessato al solo risultato vada a vedere l'ultima riga...



Nota: ho fatto molti arrotondamenti e semplificazioni; in particolare ho assunto che la distanza interatomica sia pari semplicemente alla radice cubica del volume occupato da ogni singolo atomo. Comunque ciò che volevo mostrare è l'ordine di grandezza, che secondo me ha davvero dell'incredibile: con un millimetro cubo di oro si coprono 15 milioni di chilometri, pari a circa quaranta volte la distanza dalla Terra alla Luna. Con una quantità d'oro solo dieci volte superiore si copre la distanza dalla Terra al Sole...

Ultima cosa: la collana è lunghissima, ma il suo spessore? Beh, coincide con la lunghezza di un atomo, quindi circa 0,26 milionesimi di millimetro, ovvero 260 picometri!   ▲  

Aritmetica: il Regolo Calcolatore

Sommario:

+ Contare
+ Sistemi di numerazione
+ Addizione e Sottrazione
+ Moltiplicazione
+ Divisione
+ Radice Quadrata
+ Elevamento a potenza
+ Logaritmi
– Il Regolo Calcolatore
      Uno strumento magico
      Le origini
      Doppia scala logaritmica
      il Regolo "moderno"
      Calcoli avanzati
      Qualche particolare curioso

Uno strumento magico

Ho sempre pensato che il regolo calcolatore fosse uno strumento di calcolo piuttosto limitato... fino a quando ho trovato nella biblioteca di mio padre questo libro del 1936 che ne rivela tutti i segreti:



Ci ho messo qualche giorno a capirli, ma ora posso dire... che era davvero uno strumento portentoso, in grado di fare calcoli di una complessità inaspettata.   ▲  

Le origini

Prima di iniziare a parlare del regolo calcolatore, riscrivo la definizione di logaritmo (di cui ho parlato nel capitolo precedente):

Il logaritmo decimale di un numero è l'esponente a cui elevare la base 10 per ottenere il numero dato.

Ecco come si esprime questo concetto in formule per due numeri N1 e N2, ma anche per il loro prodotto:



Fra le proprietà delle potenze (di cui invece ho parlato qui) c'è quella per cui il prodotto di due potenze di pari base è la stessa cosa di una potenza della stessa base con esponente uguale alla somma dei due esponenti di partenza. Quindi:



Dalle formule qui sopra risulta quindi che il logaritmo del prodotto è uguale alla somma dei logaritmi dei fattori. Il "trucco" alla base del funzionamento del regolo calcolatore è proprio il fatto che siamo riusciti a trasformare un prodotto in una somma!

A seguito degli studi di Nepero sui Logaritmi ci fu subito chi pensò di sfruttare l'idea in modo da velocizzare i calcoli, anche a scapito della precisione. Già nel 1623 Edmund Gunter, professore di astronomia al Gresham College di Londra, sviluppa una scala logaritmica sulla quale, con l'aiuto di un compasso, si possono eseguire graficamente moltiplicazioni e divisioni. Ecco... ma cos'è esattamente una scala logaritmica?



Si tratta di un righello in cui si riportano tacche a distanze proporzionali ai logaritmi dei numeri da 1 a 10. Nel diagramma sopra specifico che ogni tacca corrisponde al logaritmo del numero, ma la sigla "log" non è assolutamente necessaria:



Notare che a destra si scrive un 1 e non un 10: questa è una pratica utilizzata in tutti i regoli calcolatori. In pratica "si sa" che all'uno di destra corrisponde un 10; inoltre, come vedremo, in qualche caso l'uno di destra viene usato proprio come... 1 e non come 10!.

Ecco costruita la scala logaritmica! Ora ammettiamo di voler moltiplicare 1,5 per 4 con questa scala e un compasso, proprio come faceva il Gunter: basterà aprire il compasso a un'apertura corrispondente al logaritmo di 1,5 e riportare la stessa apertura sul 4. Vediamo il procedimento passo per passo:



La punta destra del compasso è posizionata sulla tacca del 1,5. La punta sinistra va messa sulla tacca del 1, perché ricordiamoci che quella tacca rappresenta il logaritmo di 1, e il logaritmo di 1 è 0. In questo modo l'apertura del compasso corrisponde alla differenza fra logaritmo di 1,5 e logaritmo di 1, quindi:

log( 1,5 ) – log( 1 ) = log( 1,5 ) – 0 = log( 1,5 )

Una volta trovata l'apertura del compasso, basta traslarlo verso destra:



Ecco che mettendo la punta sinistra del compasso sulla tacca del 4 mi ritrovo la punta destra sul 6 (ricordo che logaritmo di 1 fa 0):

log( 4 ) + [ log( 1,5 ) – log( 1 ) ] = log( 4 ) + log( 1,5 ) = log( 4 x 1,5 ) = log( 6 )

(infatti 1,5 x 4 = 6).

Con le stesse posizioni esatte avrei potuto fare il calcolo inverso: infatti con la stessa apertura corrispondente al numero 1,5, avrei potuto fare la divisione 6 : 1,5 = 4: considerando di mettere la punta destra del compasso sul 6, la punta sinistra mi avrebbe dato correttamente il quoziente cercato (alla differenza degli esponenti infatti corrisponde la divisione delle potenze).

log( 6 ) – [ log( 1,5 ) – log( 1 ) ] = log( 6 ) – log( 1,5 ) = log( 6 : 1,5 ) = log( 4 )   ▲  

Doppia scala logaritmica

Nel 1630 Edmund Wingate utilizza due scale di Gunter una di fronte all'altra per eseguire direttamente moltiplicazioni e divisioni, senza dover usare il compasso. Vediamo la moltiplicazione 1,5 x 3:



La zona rossa, nella scala inferiore, ha la stessa ampiezza del compasso che abbiamo visto sopra. Facendo partire l'origine (ossia la tacca del 1) della scala superiore proprio dalla fine della zona rossa, vedo che il limite destro della zona azzurra cade sul 4,5: infatti 1,5 x 3 = 4,5.

Questo procedimento va bene anche per calcolare numeri con ordini di grandezza diversi: es. 15 x 300 = 4500; in questi casi gli zeri in più o in meno, o gli eventuali spostamenti della virgola decimale, devono essere fatte "a mano" (in questo senso gli errori erano sempre in agguato... occorreva stare molto, molto attenti; l'ideale era capire più o meno qual era il risultato prima di calcolarlo, e cercare con il regolo solo la precisione delle cifre significative).

E se invece voglio calcolare 5 x 3? Qui nasce un problema, in quanto il tre sulla scala superiore si posiziona al di fuori della scala inferiore, quindi non riesco a leggere il risultato:



In questi casi si ricorre a un espediente: invece di moltiplicare per 3 si moltiplica per 0,3:



La zona marcata in azzurro qui sopra indica la differenza fra il logaritmo di 3 e il logaritmo di 10, quindi

log( 3 ) – log( 10 ) = log( 3 : 10 ) = log( 0,3 )

Allora basta posizionare, sul 5 della scala inferiore, non la tacca dell'uno sinistro della scala superiore, ma la tacca dell'uno destro:



In questo modo la moltiplicazione 5 x 0,3 si riesce a fare senza uscire dalle scale, e il risultato si legge sul 1,5 della scala inferiore; ma siccome abbiamo moltiplicato per 0,3 e non per 3, occorre "aggiustare" il risultato moltiplicandolo per 10: il risultato finalmente è 15!

Dicevo che fra le proprietà delle potenze (e dei logaritmi) c'è quella per cui alla divisione delle potenze corrisponde la sottrazione degli esponenti. Quindi posso calcolare la divisione 6 : 4



Dal grafico qui sopra si vede come sul 5 della scala inferiore non metto l'uno ma il 4 della scala superiore; l'uno della scala superiore si trova quindi sulla sinistra, e le aree rossa e azzurra si "sottraggono": ecco che la tacca 1 della scala superiore cade sul 1,5 della scala inferiore, determinando il risultato corretto.

Vediamo ora il calcolo "standard" (che in realtà ho scoperto essere tale solo leggendo il libro di cui ho parlato nella didascalia della foto): moltiplicazione e divisione in un colpo solo! In pratica è il calcolo di una proporzione: un numero moltiplicato per una frazione di cui sono dati numeratore e denominatore, come per esempio il calcolo dei tre mezzi di cinque (5 x 3 / 2).



Allineando il 2 della scala superiore con il 5 della scala inferiore abbiamo che la tacca del 1 sinistro della scala superiore indica il quoziente 5 : 2 = 2,5. Le zone verde e azzurra insieme danno il fattore 3, quindi è come se si stesse moltiplicando per 3 il quoziente 5 : 2. Infatti il 3 sulla scala superiore cade proprio sul 7,5 di quella inferiore, che è il risultato esatto!

Ovviamente anche con le divisioni e con i calcoli misti (moltiplicazione e divisione insieme) può capitare di uscire "fuori scala"; ma c'è sempre il modo di sistemare le scale in modo da ottenere il risultato, come abbiamo visto per la moltiplicazione.   ▲  

Il Regolo "moderno"

Grazie a successivi miglioramenti, e al fatto che a partire dalla metà del XIX secolo l'industria meccanica di precisione ne ha permesso la costruzione in serie, il regolo calcolatore è diventato uno strumento di calcolo sostanzialmente standardizzato e di ampia diffusione. I regoli calcolatori sono costituiti dai seguenti elementi:

— un corpo su cui si trovano delle scale fisse
— un'asta scorrevole con delle scale mobili
— un cursore con una o più linee di riferimento



Le scale sono di vari tipi, indicate convenzionalmente da alcune lettere. Di scale semplici, come quelle del Wingate ce ne sono sempre due, una sull'asta scorrevole (scala C) e l'altra sul corpo (D). Altre scale servono per semplificare i calcoli quando si è in presenza di quadrati, cubi; radici quadrate e cubiche; funzioni trigonometriche... ecc.. Le scale di solito sono smistate fra il davanti e il dietro dell'asta e del corpo del regolo; in questo regolo sono presenti le scale:



K  — Scala dei cubi (corpo)
A  — Scala dei quadrati (corpo)
B  — Scala dei quadrati (asta)
ST— Seni e Tangenti per angoli piccoli (asta)
T  — Scala delle Tangenti per angoli > 6° (asta)
S  — Scala dei seni (e coseni) per angoli > 6° (asta)
C  — Scala dei numeri (asta)
D  — Scala dei numeri (corpo)
DI — Scala degli inversi dei numeri (1/x) (corpo)

Nel rovescio dell'asta, in alto, compaiono tre altre scale:

CI   — Scala dell'inverso dei numeri (1/X)
CF  — scala "ripiegata", che parte da pi-greco invece che da 1
CIF — scala dell'inverso, che parte da pi-greco

Per maggiore leggibilità delle foto che seguono, espongo i calcoli in modo che tutti i numeri stiano in un breve tratto del regolo, e senza fuoriuscire dalle scale; inoltre per brevità non spiego come si determinano gli zeri o la posizione della virgola: il mio scopo è solo mostrare di cosa erano capaci gli ingegneri quando usavano un regolo!   ▲  

Calcoli avanzati

Abbiamo visto che con due semplici scale si riesce a fare un'operazione mista di moltiplicazione-divisione in un colpo solo. E se invece volessi fare una divisione-divisione? Per fare questo bisogna ricondurre l'operazione che vogliamo fare a quella "standard" di moltiplicazione-divisione usando la scala dei reciproci; con questa scala si converte la divisione per B in una moltiplicazione per 1 / B:



In verde indico i numeri di partenza e il risultato reale (calcolato con la calcolatrice); in rosso il risultato ottenuto con il regolo. Nel fare il calcolo tutti gli operandi devono essere ricondotti a numeri compresi fra 1 e 10, quindi 2100 diventa 2,1; 17 diventa 1,7 e 86 diventa 8,6. Vediamo allora come si usano le scale del regolo:



Si parte sovrapponendo il valore C (17) della scala C al valore A (2100) della scala D; come abbiamo già visto, la tacca 1 di sinistra dell'asta cade sul quoziente A/C. Portare il cursore sul valore B (86) della scala CI significa moltiplicare questo quoziente per l'inverso di B, quindi dividere tale quoziente ancora per B. La lettura del cursore sulla scala D fornisce il risultato cercato.

Ora vediamo una variante del calcolo precedente: una moltiplicazione-moltiplicazione. Anche in questo caso bisogna ricondurre l'operazione desiderata al caso standard, quindi si procede moltiplicando due fattori e dividendo per il reciproco del terzo, come indicato nelle formule:





Sovrapporre il valore B (65) della scala CI al valore A (19) della scala D significa dividere A per il reciproco di B: per fare questo allineamento si usa il cursore, perché le scale CI e D non sono adiacenti. A questo punto leggere sulla scala D il numero corrispondente al valore C (12) della scala C significa moltiplicare ancora per C: ecco trovato il risultato desiderato!

Altro tipo di calcolo: una semplice divisione, ma il numeratore è una radice quadrata.





Si sposta il cursore sul valore A (350) della scala A dei quadrati (a questa posizione corrisponde, sulla scala D normale, il valore 18,7 che è proprio la radice quadrata di 350). Se ora faccio coincidere il valore B (1,51) della scala C sulla linea del cursore, avrò che il valore della scala D in corrispondenza del 1 sinistro dell'asta corrisponde alla divisione della radice quadrata di A per B, che è il risultato cercato.

Infine un calcolo davvero complesso, che richiede l'uso di ben quattro scale diverse. Si tratta del rapporto fra una radice cubica e una radice quadrata, il tutto moltiplicato per un numero normale. Per realizzare questo calcolo occorre montare l'asta del regolo al contrario, in modo da disporre sull'asta della scala dei quadrati (la scala B) .





Si porta il cursore sul valore A (7400) della scala K dei cubi (a questa posizione corrisponde, sulla scala D normale, il valore 19,487 che è proprio la radice cubica di 7400). Si sposta poi l'asta in modo da allineare al cursore il valore B (290) della scala B. A questo punto il valore della scala D in corrispondenza del 1 sinistro dell'asta corrisponde alla divisione della radice cubica di A per la radice quadrata di B; se invece cerco il valore C (1,3) sulla scala C, il valore corrispondente sulla scala D sarà il prodotto del quoziente precedente per C, che è il valore cercato.   ▲  

Qualche particolare curioso

Esistono infinite varianti di questi tipi di calcolo, che possono coinvolgere funzioni trigonometriche, logaritmiche, esponenziali... ora capisco come facessero gli ingegneri a progettare ciò che sono stati in grado di costruire negli ultimi due secoli, prima dell'avvento dell'elettronica (almeno fino ai primi anni '70 del secolo scorso).

Fra XIX e XX secolo sono stati costruiti anche regoli calcolatori di dimensioni imponenti: avevano scale di due metri di lunghezza, e un microscopio montato sul cursore. Con questi strumenti monumentali si riuscivano ad apprezzare fino a 6 cifre significative, sia negli operandi che nei risultati!

Ultima nota interessante: quando gli astronauti sono scesi sulla Luna (1969), le calcolatrici elettroniche ancora non erano state inventate, infatti la prima calcolatrice scientifica (la HP35) è solo del 1972. Allora gli astronauti sono andati sulla Luna... portandosi dietro un regolo calcolatore! La casa costruttrice di questi regoli "extraterrestri" infatti scrive sulle confezioni dei propri regoli: "5 moon flights", cinque voli sulla Luna!   ▲